Yhtenäinen jakauma jatkaa ominaisuuksia, esimerkkejä, sovelluksia
- 2309
- 309
- Edgar VonRueden
Satunnaismuuttujalla on a Jatkuva yhtenäinen jakauma Jos arvon ottamisen todennäköisyys, äärellisellä aikavälillä [a, b] on sama kaikille saman pituisille alakohdille.
Tämä jakauma on analoginen erillisen yhtenäisen jakauman kanssa, joka osoitettiin satunnaiskokeen jokaiselle tulokselle sama todennäköisyys, mutta tässä tapauksessa otettava muuttuja on jatkuva. Esimerkiksi koe, joka koostuu satunnaisen reaali -luvun valitsemisesta arvojen A ja B välillä, seuraa yhtenäistä jakautumista. Täällä sinulla on kaavio:
Kuvio 1. Kaavio jatkuvan normalisoidun tasaisen jakauman tiheysfunktiosta Matemaattisessa merkinnässä jatkuvalla yhtenäisellä jakautumisella on tiheysfunktio, joka on määritelty funktiona kappaleiksi tai osiin, jotka voidaan kirjoittaa seuraavasti:
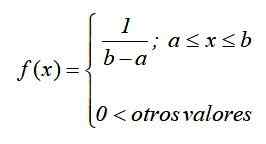
Tämän toiminnon kaavio, joka tunnetaan nimellä Käyrä tai tiheystoiminto, Se on suorakulmio, joten jatkuva yhtenäinen jakauma tunnetaan myös nimellä suorakulmainen jakauma Ja se on yksinkertaisin jatkuvasta jakautumisesta.
Todennäköisyysjakauman kaavion alla oleva alue on yhtä suuri kuin 1 ja ottaa aina positiivisia arvoja. Yhtenäinen jakauma täyttää nämä kriteerit. Ei ole tarpeen integroida suoraan varmistaakseen, että pinta -ala on 1, koska kuvan 1 varjostetun suorakulmion pinta -ala voidaan laskea kaavalla:
Pinta -ala = pohja x korkeus = (b - a) x [1/(b - a)] = 1
Tiheyskäyrän alla olevan alueen tunteminen on erittäin tärkeää, koska alueen ja tapahtuman todennäköisyyden välillä on suhde, joka tässä jakautumisessa määritetään seuraavassa osassa.
Jatkuvat yhtenäiset jakautumisominaisuudet
Jatkuvalle yhtenäiselle jakautumiselle on ominaista:
Tiheysfunktio
Olkoon x jatkuva satunnaismuuttuja, joka kuuluu aikaväliin [a, b], sitten: sitten:
Se voi palvella sinua: lineaariset muunnokset: Ominaisuudet, mitkä ovat käyttö, tyypit, esimerkit=\frac1b-a)
Jakelufunktio
Jakelufunktion avulla todennäköisyys, että satunnaismuuttuja X vie X -arvon välin mahdollisista arvoista [a, b]. Jatkuvaa jakautumista varten se lasketaan yleensä tällä tavalla:
=\int_a^xf(x)dx)
Jatkuvan yhtenäisen jakautumisen tapauksessa mainitun todennäköisyys F (x) vastaa suorakulmion aluetta, jonka pohja on (x-A) ja sen korkeus on (B-A):
=\int_a^x\left&space;(\frac1b-a&space;\right&space;)dx=\fracx-ab-a)
Matemaattisesti, jos f (x) = pr (x = x), seuraava funktio määritetään osilla, edellisen tuloksen mukaan:
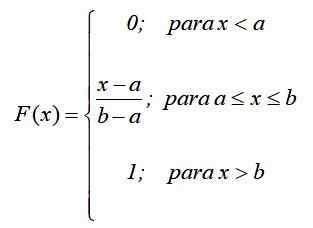
Tällä tavalla se on aiemmin sanottu: Todennäköisyys riippuu vain (x-a) arvosta eikä sen sijainnista aikavälillä [a, b]. Jakelufunktion kaavio on:
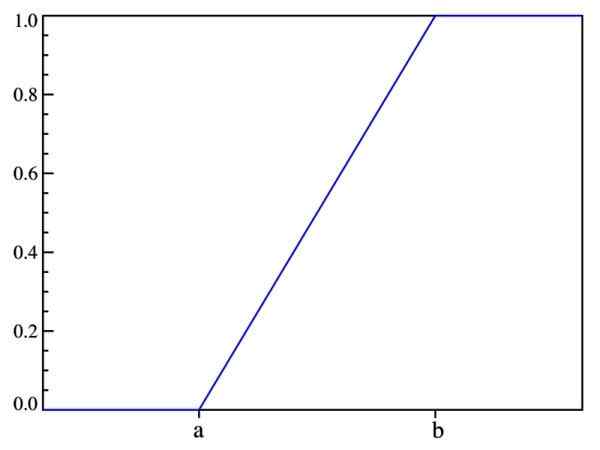Kuva 2. Jakelufunktion kaavio F (x). Lähde: Wikimedia Commons. Odotettu arvo, varianssi ja keskihajonta
Saatuaan lukuisia kokeita jatkuvan satunnaismuuttujan kanssa, sen keskiarvoa kutsutaan odotettu arvo, Se on merkitty nimellä E (x) ja se lasketaan seuraavalla integraalilla:
=\int_a^bxf(x)=\int_a^b\left&space;(\frac1b-a&space;\right&space;)xdx=\left&space;(\frac1b-a&space;\right&space;)\frac(b^2-a^2)2=\fraca+b2)
V (x) = e (x2) - ex)2
Siksi:
=\left&space;[\int_a^bx^2f(x)dx&space;\right&space;]-\left&space;(\fraca+b2&space;\right&space;)^2=\left&space;[\int_a^bx^2\left&space;(\fracb-a2&space;\right&space;)&space;dx\right&space;]-\left&space;(\fraca+b2&space;\right&space;)^2)
=\frac(b-a)^212)
D (x) = √ V (x)
=\sqrt\frac(b-a)^212)
Mediaani, muoti, symmetria ja rostos
Voidaan helposti varmistaa, että mediaani, joka on yhtenäisen jakauman keskeinen arvo, on yhtä suuri kuin keskiarvo, ja koska ei ole arvoa, joka toistetaan enemmän kuin toiset, koska kaikki ovat yhtä todennäköisiä aikavälillä [a, b ], muotia ei ole olemassa.
Symmetrian suhteen yhtenäinen jakauma on symmetrinen ja rostos, jonka määrä keskustan ympärillä olevat arvot ovat keskittyneet -6/5.
Voi palvella sinua: mitkä ovat kehän 7 elementtiä?Esimerkit
Erilaisia tilanteita voidaan mallintaa jatkuvan jakautumisen kautta ja ennustaa siten heidän käyttäytymisensä. Tässä on joitain esimerkkejä:
Esimerkki 1
Yritys, joka tarjoaa sähköpalvelua.0 V ja 125.0 V. Tämä tarkoittaa, että kotimaisessa laukauksessa on mahdollista saada kaikki kyseiseen aikaväliin kuuluva jännitearvo.
Sitten, kuten yllä nähtiin, tiheysfunktion kuvaaja on punainen suorakulmio:
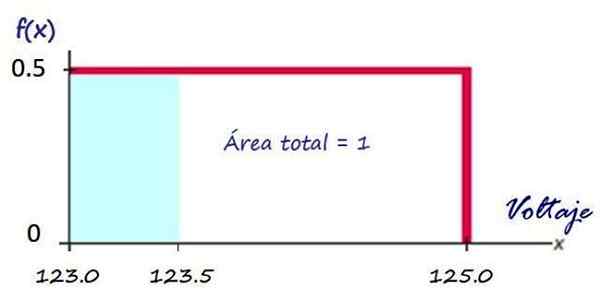Kuva 3. Sähköyhtiön toimittaman jännitteen tiheystoiminto. Lähde: f. Zapata. Jännitteen todennäköisyyden laskeminen annetulla aikavälillä on erittäin helppoa, esimerkiksi mikä on todennäköisyys, että yritys lähettää jännitteen alle 123.5 V?
Tämä todennäköisyys vastaa sinisen varjostetun suorakulmion aluetta:
P (x<123.5) = (123.5 −123.0)x 0.5 = 0.25
Ja mikä on todennäköisyys, että toimitettu jännite on suurempi kuin 124.0 V?
Koska kokonaispinta -ala on yhtä kuin 1, etsittu todennäköisyys on:
P (x> 124.0 V) = 1 - (1 × 0.5) = 0.5
On järkevää, vuodesta 124.0 on juuri arvon keskipiste.
Esimerkki 2
Tietyllä satunnaismuuttujalla X jakauma on yhtenäinen [0,100]. Päättää:
a) Todennäköisyys, että x: n arvo on alle 22.
b) Todennäköisyys, että x on arvot välillä 20 - 35.
c) Tämän jakauman odotettu arvo, varianssi ja standardipoikkeama.
Vastaa
Se määritetään samanlaisen kuin edellinen esimerkki, mutta ensin meidän on määritettävä suorakulmion korkeus, muistaen, että kokonaispinta -alan on oltava yhtä suuri:
Pinta -ala = 100 × korkeus = 1
Siksi suorakulmion korkeus on yhtä suuri kuin 1/100 = 0.01
Voi palvella sinua: Decagon: säännöllinen, epäsäännöllinen, ominaisuudet, esimerkitP (x<22) = 22×0.01 = 0.22
Vastaus b
Pyydetty todennäköisyys vastaa suorakulmion aluetta, jonka leveys on (35 - 20) ja jonka korkeus on 0.01:
P (22 Jos haluat siirtyä suoraan yllä olevaan jakelufunktioon, sinun on vain korvattava arvot: P (20≤x≤35) = F (35) -F (20) F (x): n kanssa: F (x) = (x-a) / (b-a) Esitettävät arvot ovat: A = 0 B = 100 F (35) = (35-0) / (100-0) = 0.35 F (20) = (20-0) / (100-0) = 0.kaksikymmentä P (20≤x≤35) = 0.35-0.20 = 0.viisitoista Odotettu arvo on: E (x) = (a+b)/2 = (100+0)/2 = 50 Varianssi on: V (x) = (B-A)2/12 = (100-0)2/12 = 833.33 Ja keskihajonta on: D (x) = √833.33 = 28.87 Tämä jakauma on hyödyllinen, kun tilastolliset simulaatioprosessit suoritetaan tai työskennellessään tapahtumissa, joiden ulkonäön esiintymistiheys on säännöllinen. Jotkut ohjelmointikielet tuottavat satunnaislukuja välillä 0 ja 1, ja kuten aiemmista esimerkeistä voidaan nähdä, seuraavien todennäköisyyksien jakautuminen on yhtenäinen. Tässä tapauksessa harkittava aika on [0,1]. Jos sinulla on kokeilu, jossa tapahtumissa on säännöllisyyttä, kuten edellä selitetään, voit periaatteessa antaa jokaiselle samalle todennäköisyydelle esiintymisen todennäköisyyden. Tässä tapauksessa yhtenäisen jakauman todennäköisyysmalli tarjoaa tietoa analyysistä. Yhtenäistä jakaumaa käytetään myös havaittujen arvojen ja muuttujan todellisten arvojen välisten erojen pyöristämisessä olettaen virheen tasaisen jakautumisen tietyllä aikavälillä, pyöristämisen mukaan, yleensä -0,5 - - - +0,5.Vastaus C
Sovellukset
Satunnaisluvut
Mielivaltainen jakaumanäytteenotto
Virheen pyöristäminen
Viitteet