Tilastollinen väestökonsepti, tyypit, esimerkit

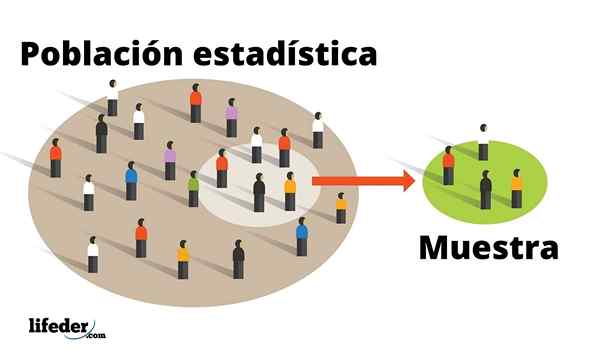
Se tilastollinen väestö Se on täydellinen kollektiivinen tai elementtijoukko, jolla on yhteisiä ominaisuuksia ja jonka haluat opiskella. Nämä elementit voivat olla ihmisiä, eläviä olentoja, elottomia esineitä, tapahtumia, asenteita joihinkin monimuotoisiin tapahtumiin ja yrityksiin.

Esimerkkejä populaatioista ovat koko maan tai kaupungin asukkaat, tehtaan tuottamat artikkelit yhden päivän jälkeen tai tähtiä maitomaisella tavalla. Se voidaan myös luokitella tilastolliseksi väestöksi kaikille yliopiston opiskelijoiden saamille pätevyyksille koulun lopussa.

Tilastollinen väestö voi koostua joukosta ihmisiä, asioita tai tapahtumia, joita haluat opiskella

Tutkija on se, joka päättää, mitkä ovat väestön kiinnostuksen ominaisuudet opiskelemaan. Siksi, koska se on niin laaja mahdollisuuksia, populaatiot luokitellaan jollain erinomaisella ominaisuudella, kuten niiden koko.

Tämä määrittelee yleisimmän tavan luokitella tilastolliset populaatiot, joten populaatioiden sanotaan yleensä olevan ääretön tai rajallinen. On kuitenkin myös muita erottuvia ominaisuuksia, aina suoritettavan tutkimuksen kannalta.

Tällaiset ominaisuudet on aiemmin määritelty sen varmistamiseksi.

Populaatioita tutkitaan yleensä huolellisesti valitun näytteen kautta: tämä on edustava alajoukko, jonka pienempi koko on helpompaa käsitellä. Laajennuksen mukaan näytteen ominaisuudet vastaavat kapean marginaalin sisällä olevan väestön ominaisuuksia, jotka tutkija vahvistaa mukavuuteen tilastollisilla tekniikoilla.

Tilastollisten populaatioiden tyypit

Periaatteessa tilastollisia populaatioita voi olla yhtä monta tyyppiä kuin ominaisuuksia, he haluavat sisällyttää määritelmään.

Se voi palvella sinua: mikä on suhteellinen taajuus ja miten se lasketaan?

On myös huomattava, että jotkut populaatiot sopivat ilman ongelmia useamman kuin yhden jäljempänä mainittuun luokkaan:

Ääretön populaatio

Ne ovat teoreettisia populaatioita, koska ne sisältävät äärettömän määrän elementtejä. Joissakin populaatioissa on kuitenkin niin monia elementtejä, joita käytännössä pidetään äärettömänä, koska kokonaismäärä on erittäin vaikea määrittää.

Esimerkit

-Real numerosarja.

-Hapen atomien lukumäärä huoneen ilmassa.

Äärelliset väestöt

Maan opiskelijoiden kokonaismäärä on rajallinen väestö

Heillä on rajoitettu määrä komponentteja, ja niiden lukumäärä voi olla melko suuri tai päinvastoin, pieni.

Esimerkki

-Yrityksen työntekijöiden lukumäärä.

-Maan opiskelijoiden kokonaismäärä.

Todelliset populaatiot

Se viittaa ryhmään elementtejä, joiden olemassaolo on olennainen tai myös tapahtuman konkreettisiin havaintoihin.

Esimerkit

-Olemassa olevia sinisiä valaita.

-Kuluttajien asenne uuteen tuotteeseen markkinoilla.

Hypoteettinen väestö

Tässä luokassa on havaintoja mahdollisista tapahtumista ja myös psykologisista ominaisuuksista.

Esimerkki

-Ihmisryhmän ahdistuneisuustasot katastrofin mahdollisuudessa.

Vakaa väestö

Nämä ovat populaatioita, joiden ominaisuuksia ylläpidetään ajassa ja tilassa tai eivät vaihtele merkittävästi.

Esimerkki

-Planeettojen kiertojakso.

Epävakaa populaatio

Epävakaalla populaatiolla on yksi tai useampi muuttuva ominaisuus sekä ajan että avaruuden aikana.

Esimerkki

-Kaupungin joukko ihmisiä, jotka kuluttavat tiettyä soodabrändiä esitetty uudella värillä tai maulla ...).

Voi palvella sinua: mitkä ovat sisäiset vaihtoehtoiset kulmat? (Harjoituksilla)

Riippuvaiset populaatiot

Ne liittyvät yhteen tai useampaan ominaisuuteen, ja siksi ne voivat vaihdella muuttuessaan joko kokonaan tai osittain.

Esimerkki

-Tuotteiden myynti, jolla on väestöryhmä, jotka riippuvat muun muassa mainonnasta tehdystä investoinnista.

Binomipopulaatiot

Tämä väestö pyrkii määrittämään tietyn ominaisuuden läsnäolon tai puuttumisen.

Esimerkki

-Ihmisravinnoksen kivennäisvesikemiassa koskevissa tutkimuksissa on yleistä huomauttaa jonkin yhdisteen, kuten natriumkloridin tai kalsiumkarbonaatin, läsnäolosta.

Polynomipopulaatio

Polynomipopulaatioissa on tarkoitus suorittaa ominaisuusjoukko.

Esimerkki

-Peruskoulun opiskelijoiden ikä, korkeus ja paino.

Satunnaiset populaatiot

Näissä populaatioissa tapahtuu muutoksia, jotka johtuvat sattumasta tai olosuhteista, jotka pakenevat ihmisen valvonnasta.

Esimerkki

-On teollisia prosesseja, joissa odottamattomat variaatiot vaikuttavat lopputuotteiden laatuun. Jos ukkosen viikon aikana sähkön tarjonnassa tapahtui epäonnistumisia, mikä vaikutti pahvilävihastehtaaseen, mahdollisesti kyseisen viikon tuotanto ei ole samanlaatuinen kuin säännöllinen tuotanto.

Esimerkkejä tilastollisesta väestöstä

Alla on havainnollistava luettelo erityypeistä, joita voi esiintyä lukuisilla alueilla. On tärkeää korostaa jälleen, että sama väestö voi kuulua useampaan kuin yhteen kuvatuista tyypeistä, koska sillä on yhteisiä ominaisuuksia.

- Kissan kokonaisväestö maassa (todellinen ja ääretön väestö).

- Vesimolekyylit Atlantin valtameressä (se on todellinen ja ääretön populaatio, koska se sisältää useita elementtejä, joita käytännössä on mahdotonta niiden kokonaismäärä).

Voi palvella sinua: fraktiot vastaavat 3/4

- Kaikki maan päällä olevat virukset (todellinen ja ääretön populaatio).

- Ennenaikaisten syntymien lukumäärä seuraavan vuosineljänneksen aikana (hypoteettinen väestö, koska syntymiä ei ole vielä tapahtunut, ja se on myös rajallinen).

- Mahdollisten metsäpalojen (hypoteettinen ja rajallinen populaatio) seuraavan kuivuuskauden määrä seuraavan kuivuuskauden määrä.

- Maitomaisen tavan ytimessä olevien tähtien lukumäärä (rajallinen ja vakaa väestö, koska tähtien lukumäärä pysyy vakiona pitkään ja on myös todellinen).

-Kaikkien ensisijaisten lukujen sarja (ääretön, vakaa ja todellinen populaatio).

- Kolesterolitaso Euroopan unionin maiden väestössä (äärellinen, riippuvainen, todellinen, epävakaa väestö).

- Selviytyneiden lukumäärä Vesubion purkautuessa (hypoteettinen, rajallinen, epävakaa väestö).

Viitteet

1. Tilastot käsitteiden sanasto. Palautettu: psi.Uba.AR.
2. Jimin tilastot. Populans, parametrit ja näytteet päätelmätilastoissa. Palautettu: StatisticsByjim.com.