Diskreetti jakauma
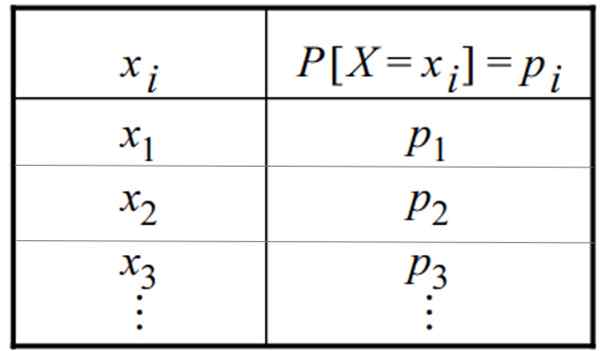
- 1695
- 362
- Dr. Travis Reichert
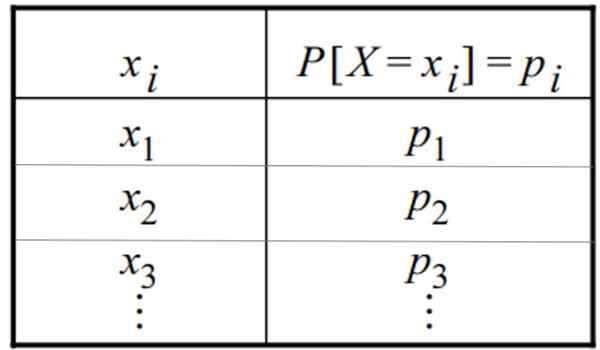 Hienovaraisen todennäköisyyden jakautumisen taulukko. Lähde: f. Zapata
Hienovaraisen todennäköisyyden jakautumisen taulukko. Lähde: f. Zapata Mikä on hienovarainen jakelu?
Eräs hienovarainen jakelu Todennäköisyydet ovat funktio F (xYllyttää) se osoittaa erillisen muuttujan jokaiselle arvolle: x1, x2, x3,... xYllyttää, tietty esiintymisen p (x = xYllyttää-A. Tätä toimintoa kutsutaan myös "todennäköisyys massafunktioksi".
Diskreetti todennäköisyysjakauma voidaan antaa taulukon tai grafiikan muodossa. Taulukossa on tämä yleinen muoto, jossa muuttuja näkyy yhdessä sarakkeessa ja sen vastaava todennäköisyys toisessa:
Todennäköisyysmassat jakavat seuraavat yleiset ominaisuudet:
- Todennäköisyys pYllyttää minkä tahansa X -tapahtumanYllyttää Se on välillä 0 ja 1, jopa jotkut näistä raja -arvoista: 0 ≤ x ≤ 1.
- P (x = xYllyttää) = PYllyttää Ota vain positiivisia arvoja, siksi: p (x = xYllyttää) ≥ 0.
- On totta, että ∑ p (xYllyttää) = 1 kaikille mahdollisille x -arvoille.
Todennäköisyysjakauma kuvaa populaation käyttäytymistä, jota sen parametrit kuvataan: keskimääräinen μ, varianssi σ2 ja keskihajonta S = σ σ2.
Seuraavaksi kuvataan merkittävimmät erilliset jakaumat:
Virka-asujen jakelu
Se on kaikkien yksinkertaisin hienovarainen jakelu. Siinä muuttuja voi ottaa "n" erilliset arvot: x1, x2, x3,... xYllyttää, Kaikki samalla todennäköisyydellä. Tässä tapauksessa jakauma annetaan:
Binomijakauma
Se koskee kokemuksia, joissa on vain kaksi mahdollista ja toisiaan poissulkevia tuloksia, joita yleensä kutsutaan "menestykseen" ja "epäonnistumiseen", merkittynä E ja F. Se tosiasia, että tapahtumaa kutsutaan "menestykseen", ei välttämättä tarkoita, että se on hyvä asia, se on pikemminkin mielivaltainen nimitys.
Menestyksen P (e) todennäköisyys ”N” -harjoituksissa merkitään p: ksi ja epäonnistumisen p (f), kuten q = 1 - p.
Jos "X" edustaa tiettyä määrää menestyksiä "N" riippumattomissa kokeissa, on totta, että: 0 ≤ x ≤ n. Ja tapahtuman esiintymisen P (x) todennäköisyys lasketaan seuraavan kaavan kautta:
Se voi palvella sinua: neliö senttimetriä neliömetriin (cm² - m²)Missä x = 0, 1, 2, 3 ..., n ja symboli (!) tarkoittaa "tekijää":
x! = x ∙ (x - 1) ∙ (x - 2) ∙ (x - 3)… 1
0 -! = 1
Poisson -jakelu
Tässä jakautumisessa satunnaismuuttuja X osoittaa, kuinka monta kertaa tapahtuma tapahtuu jollain aikavälillä, mikä voi olla aikaa, etäisyyttä tai muuta. Tapahtuman tapahtumat ovat satunnaisia, riippumattomia ja jakautuvat tasaisesti koko kyseisen ajanjakson ajan.
Kun nämä olosuhteet, todennäköisyys, joka riippuu μ -tapahtumien keskiarvosta ja Eulerin lukumäärästä ”E”, lasketaan:
Tämän jakauman tapahtumien mahdollisuudet ovat pienet, joten sitä kutsutaan "harvinaisten tapausten laki".
Binomial jakautumislähestymistapa
Poissonin jakauma toimii lähestymistapana binomijakaumaan, kun N on suuri (N≥ 100) ja P on pieni (NP ≤ 10). Tässä tapauksessa keskimääräinen μ lasketaan seuraavasti:
μ = n ∙ p
Hypergeometrinen jakauma
Sitä käytetään, kun todennäköisyydet eivät ole riippumattomia, ts. Kokeen suorittamisen jälkeen olosuhteet eivät ole taas samat. Näin tapahtuu, kun upotetaan näytteitä ilman vaihtamista populaatiosta, joten binomijakaumaa ei voida enää käyttää.
Jos populaatio koostuu kahden tyyppisistä esineistä, jotka ovat erilaisia kuin B, ja satunnaisissa esineissä ja ilman korvaavia, tyypin A X -objektien todennäköisyys ovat: ovat:
Jos a ja b ovat kunkin tyypin objekteja vastaavat määrät, läsnä populaatiossa.
Jos populaatio on kuitenkin erittäin suuri, vaikka korvaavia ei olisi, sama elementti on vaikea valita useammin kuin kerran, joten sekä jakautumiset: binomiaalinen ja hypergeometrinen tuottavat samanlaisia tuloksia.
Voi palvella sinua: Kuutiot: Kaavat, yhtälöt, esimerkit, harjoituksetEsimerkit
Kolikot käynnistyvät
CO -LAUNNAT ovat erittäin havainnollistavia esimerkkejä:
-Rehellisen valuutan käynnistäminen ja saat kasvot. On tiedossa, että yhdellä pinnalla on ½ todennäköisyys lähteä ja risti (0 kasvot), sama. Jakelu on esitetty tässä taulukossa:
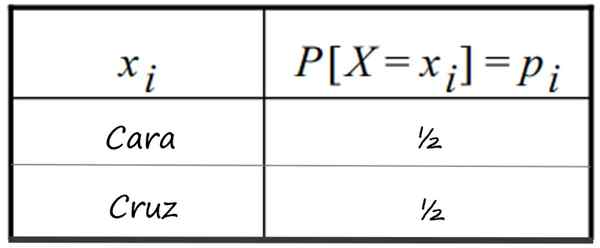 Erillinen todennäköisyysjakelu taulukko, joka seuraa yhden rehellisen valuutan käynnistämistä. Lähde: f. Zapata
Erillinen todennäköisyysjakelu taulukko, joka seuraa yhden rehellisen valuutan käynnistämistä. Lähde: f. Zapata -Samanaikainen laukaus kaksi Rehelliset kolikot ja mahdolliset kasvot, jotka voidaan saada.
 Erillinen todennäköisyysjakelu taulukko, joka seuraa kahden rehellisen valuutan käynnistämistä, jotta saadaan minkä tahansa kasvot tai ei. Lähde: f. Zapata
Erillinen todennäköisyysjakelu taulukko, joka seuraa kahden rehellisen valuutan käynnistämistä, jotta saadaan minkä tahansa kasvot tai ei. Lähde: f. Zapata Muuttujat yhtenäisellä jakautumisella
-Kokonaislukuluvun valinta, joka on tasainen tai pariton: jokainen on todennäköisyys, että ½ valitaan kokonaislukujoukossa.
-Rehellisen noppan lanseeraus. Tässä tapauksessa on 6 numeroitua kasvoja ja jokaisella on sama todennäköisyys lähteä: 1/6.
-Kehyksen valinta tentin suorittamiseksi, valittavana N -ongelmien välillä, jos ne kaikki ovat yhtä todennäköisiä.
Muuttujat binomijakaumalla
-Kasvojen lukumäärä, jotka ilmestyvät käynnistämällä rehellinen kolikko.
-250 perheen väestöstä niiden lukumäärä, joilla on 2 lasta.
-Selviytyvien ruusupuiden määrä puutarhuri 20 rosalaa puutarhassa.
-50 potilasta, joiden lukumäärä oli negatiivinen reaktio lääkkeeseen, jossa oli 50 potilasta.
-Opiskelijoiden lukumäärä, joka on hyväksytty todennäköisyyskokeessa, ryhmästä, joka koostuu 100 opiskelijasta.
Muuttujat Poisson -jakauman kanssa
-Puhelujen lukumäärä minuutissa Puhelinkeskus Yritys.
-Tietyn maantieteellisen alueen suurten maanjäristysten lukumäärä vuodessa.
-Tornaadojen lukumäärä, jotka vaikuttivat tietylle alueelle viime vuoden aikana.
-Sienellä tartunnan saaneiden puiden lukumäärä, metsän neliön hehtaaria kohti.
Muuttujat, joissa on hypergeometrinen jakauma
-Numeroiden menestykset tai voittaneet yhdistelmät uhkapeleissä.
Voi palvella sinua: samanaikaiset vektorit: ominaisuudet, esimerkit ja harjoitukset-Tietyn määrän naaraita tai uroksia valinta N -kalan N -kalan näytteessä.
Ratkaisut
Harjoitus 1
Tutkimus määritteli, että satunnaisesti älypuhelimilla olevilla aikuisilla 54% heistä käyttää niitä luokassa tai kokouksissa. Haluat löytää todennäköisyyden, että satunnaisesti 8 henkilöä älypuhelimella, tarkalleen 6 heistä käyttää niitä luokassa tai kokouksissa.
Ratkaisu
Tämä koe on yhtä mieltä binomikokeesta, koska tulos on binaarinen: henkilö ottaa puhelimen luokassa tai ei ota sitä pois. Sitä, että henkilö käyttää luokassa olevaa puhelinta.
Siinä tapauksessa: p = 0.54 ja Q = 1- 0.54 = 0.46.
Koska 8 ihmistä on valittu satunnaisesti, niin n = 8 ja x: n arvo on 6, siksi tarvittavat arvot ovat käytettävissä niiden korvaamiseksi binomialjakauman kaavassa:
Harjoitus 2
Viime vuonna klinikka rekisteröi 4221 syntymää. Tämän ainutlaatuisen tiedon avulla määritä todennäköisyys, että syntymiä on 15 päivässä. Onko tämä tapahtuma harvinainen?
Ratkaisu
Poisson -jakautumista käytetään, koska sitä pyydetään määrittämään tapahtuman todennäköisyys, joka tapahtuu aikavälillä. Tässä tapauksessa muuttuja on syntymämäärä ja aikaväli on 1 päivä.
Poisson -jakelukaava tarvitsee keskimääräisen syntymän päivässä, joka on helposti laskettu:
Siksi x = 15 syntymän todennäköisyys on:
Tulos voidaan ilmaista selkeyden prosentteina: 6.42% todennäköistä, että joka päivä tapahtuu tarkalleen 15 syntymää. Tapahtuma on epätodennäköistä, vaikka ei missään tapauksessa mahdotonta.


=\frac1n)
=\fracn!\left&space;(&space;n-x&space;\right&space;)!\cdot&space;x!\cdot\:p^x\cdot&space;q^n-x)
=\frac\mu&space;^x\cdot&space;e^-\mu&space;x!)
=\fracA!\left&space;(A-x&space;\right&space;)!\cdot&space;x!\cdot&space;\fracB!\left&space;(B-n+x&space;\right&space;)!\cdot&space;\left&space;(n-x&space;\right&space;)!\div&space;\frac\left&space;(A+B&space;\right&space;)!\left&space;(A+B-n&space;\right&space;)!\cdot&space;n!)
=\frac8!\left&space;(8-6&space;\right&space;)!\times&space;6!\times&space;0.54^6\times&space;0.46^\left&space;(8-6&space;\right&space;)=\frac8!2!\times&space;6!\times&space;0.54^6\times&space;0.46^2=0.147)

=\frac11.56^15\times&space;e^-11.5615!=0.0642)