Clausius-Clapeyron-yhtälö, mihin se on esimerkkejä, harjoituksia
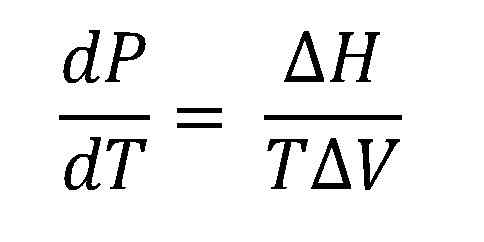
- 2178
- 435
- Arthur Terry II
Se Clausius-Clapeyron-yhtälö Se liittyy höyrynpaineen ja lämpötilan muutoksiin vaiheen tai tilansiirtymän muutoksessa. Koskee sublimointeja, haihtumisia, sulautumisia tai jopa kiteisten vaiheiden muutoksia. On syytä mainita, että tämä yhtälö koskee puhdasta ainetta, joka on tasapainossa.
Tämä yhtälö johtuu aineen termodynaamisista laeista ja P-T-kaavioista, joissa havaitaan rinnakkaiselon linjaa; Se, joka erottaa kaksi eri vaihetta (nestemäinen höyry, kiinteä-neste jne.-A. Tämän linjan siirtämiseksi lämmön voito tai menetys on välttämätöntä, kuten höyrystymisen entalpia, ΔHHöyry.
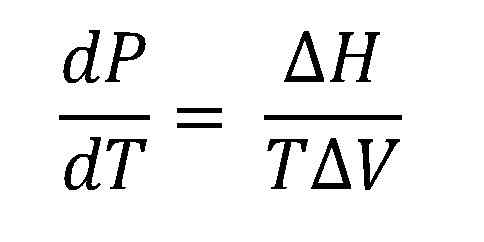 Clausius-Clapeyron-yhtälö. Lähde: Gabriel Bolívar.
Clausius-Clapeyron-yhtälö. Lähde: Gabriel Bolívar. Korkeampi kuva näyttää Clausius-Clapeyron-yhtälön ennen integrointia. Normaalisti sitä käytetään yleensä nestemäishöyryjärjestelmiin, joissa AH: ta käytetäänHöyry Ja haluat laskea, mikä nesteen höyrynpaine on tietyssä lämpötilassa. Se myös laskee ΔHHöyry tietyn nesteen lämpötila -alueella.
Clausisu-clapeyron-yhtälöä käytetään myös melko usein haihtuvien kiinteiden aineiden paineen muutoksiin; Eli sublimointiarvoa pidetään ΔHsub.
[TOC]
Mikä on Clausisu-clapeyron-yhtälö?
Paineiden ja höyrystymispaineiden paineiden laskeminen
Ylhäältä Clausius-Clapeyronin yhtälöstä on lopulta tehty joitain matemaattisia näkökohtia integraation lopulta suorittamiseksi. Esimerkiksi nestemäishöyryjärjestelmässä oletetaan, että ΔHHöyry Se ei vaihtele lämpötilan mukaan ja että ΔV vastaa yksinomaan höyryn tilavuutta, halveksien nesteen tilavuutta (vhöyryä-Vnestemäinen = Vhöyryä-A.
Olettaen, että höyry käyttäytyy ihanteellisena kaasuna ja integroituna, saadaan Clausius-clapeyronin yhtälö:
Voi palvella sinua: haihtuvuus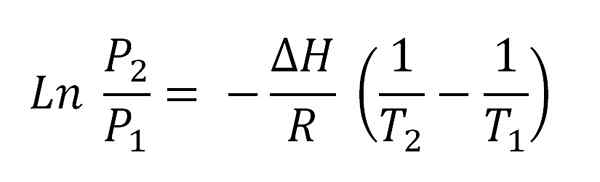 Clausius-Clapeyron-yhtälö integroitu.
Clausius-Clapeyron-yhtälö integroitu. Tämä yhtälö vastaa viivan yhtäkään, joka on graafinen:
Ln p vs 1/t
Ja jonka negatiivinen kaltevuus on (ΔH/r). Tämän yhtälön täyttämiseksi ΔH: n on oltava vakio lämpötilavälillä (T2-T1), jossa höyrypaineet mitataan tasapainossa nesteen kanssa.
Tällä tavalla, jos oletetaan, että ΔH vaihtelee vähän pienten lämpötilaväleiden sisällä, on mahdollista käyttää tämän viivan yhtälöä ennustamaan nesteen höyrynpaineiden muutoksia; Ja vielä enemmän, voit määrittää sen höyrystymisen ΔH.
Mitä suurempi lämpötilojen väliajot, sitä suurin kokeellisen tiedon yhtälön poikkeama ja sitä vähemmän se toteutetaan.
Vaihemuutosten määrittäminen
Siten Clausius-Clapeyronin yhtälöstä tulee tangenttiviivan kehitys rinnakkaiseloon kahden fysikaalisen vaiheen välillä, mikä havaitaan missä tahansa aineen P-T-kaaviossa.
Jos vaihemuutos tapahtuu, kaltevuudella tapahtuu muutos, ja ΔH ei ole sama. Siksi, kun osoittavat voimakkaita poikkeamia ja yhtälö epäonnistuu, se on merkki siitä, että lämpötilavälillä aine kokee toisen vaihemuutoksen. Eli se lakkaa olemasta nestemäistä höyryjärjestelmää, koska se siirretään rinnakkaiseloon, joka vastaa kiinteän ja nesteen tai kiinteän höyryn tasapainottamista.
Käytä esimerkkejä
- Meteorologiassa on käytetty Clausius-Clapeyron-yhtälöä pilvien käyttäytymisen tutkimiseen, jopa muilla planeetoilla tai kuussa ilmakehillä.
Voi palvella sinua: glukonihappo: rakenne, ominaisuudet, synteesi, käyttö- Sitä on käytetty määrittämään useiden metallien, kuten natrium ja gallium.
- Sitä on käytetty myös aineiden, kuten kaasumaisen kloorin, hiilitetrakloridin, nestemäisen veden, jään ja jodin, höyrystymisen entalpia.
- Se on myös tutkinut faasimuutoksia kiteisiin rakenteisiin. Tässä viimeisessä esimerkissä Clausius-Clapeyronin integroitu yhtälö näyttää huomattavan erilaiselta, koska samoja näkökohtia, jotka on otettu nestemäiselle höyryjärjestelmälle, ei voida tehdä AV: lle. Tilavuuden vaihtelut vaiheesta toiseen tällä kertaa ovat pienet.
Ratkaisut
- Harjoitus 1
Jään höyrynpaine on 4.58 torr 0 ° C: ssa ja 1.95 torr a -10 ° C. Mikä on sublimointisi entalpia siinä lämpötila -alueella?
Huomaa, että meillä on kaksi painetta ja kaksi lämpötilaa:
P1 = 4.58 torr
P2 = 1.95 torr
T1 = 0 ° C + 273 = 273 K
T2 = -10 ° C + 273 = 263 K
Muunna lämpötilayksiköt ° C: sta K: ksi, koska kaasujen vakiona R: llä on K: n yksiköissä:
R = 8.314 J/K
Siten käytämme integroitua clausius-clapeyron-yhtälöä ja kirkasta ΔHsub, joka pysyisi:
ΔHsub = -Rln (p2/P1) / (1 / t2 - 1 /t1-A
Lisää mukavuutta korvaa vain numeroilla, mutta tietäen, että lopullinen yksikkö on joule:
ΔHsub = -(8.314) LN (1.95/4.58)/(1/263 - 1/273)
= 50.97 J
Tai 51.07 j ottaen huomioon muutama desimaali. Tämä arvo esittelee värähtelyjä väliajoista t2-T1 ja tiettyjä höyrypaineita.
- Harjoitus 2
Etanolin kiehumispiste paineessa 760 torr (1 atm) on 78.3 ° C, ja sen höyrystymisen entalpia on 39.3 kJ. Mikä on höyrypaine 46 ° C: n lämpötilassa?
Se voi palvella sinua: Tantalus: rakenne, ominaisuudet, käytöt, hankkiminenTunnistamme tiedot:
P1 = 760 torr
P2 = ?
T1 = 78.3 ° C + 273 = 351.3 K
T2 = 46 ° C + 273 = 319 K
ΔHHöyry = 39.3 kJ tai 39300 J
Joten meidän on puhdistettava p2 integroidun Clausius-Clapeyron-yhtälön. Jälleen yksiköt jätetään mukavuuden vuoksi ja laskelmat kehitetään askel askeleelta:
Ln (p2/P1) = -(ΔHHöyry/R) (1/t2 - 1/t1-A
Ln (p2/760) = -(39300/8.314) (1/319 - 1/351.3)
Ln (p2/760) = -1.36
Eksponentiaalisen funktion soveltaminen yhtälön molemmille puolille P: n puhdistamiseksi2 meillä tulee olemaan:
E (ln p2/760) = E(-1.36)
P2/760 = 0.256
P2 = 0.256 (760)
= 195 torr
Alemmassa lämpötilassa (46 ° C) alempi höyrynpaine (195 torr). Itse asiassa etanolilla on 760 torr -paine 78: een.3 ° C, puhumme sen normaalista kiehumispisteestä. Tämä on kaikkien nesteiden odotettu käyttäytyminen
Yleensä tämän tyyppiset Clausius-Clapeyron-harjoitukset koostuvat P: n puhdistamisesta2, T2 tai höyrystymisen tai sublimaation ΔH. Laskelmat muuttuvat merkittävästi, kun myös AV: tä tulisi harkita, etenkin kun kyse on kiinteiden nesteen järjestelmistä tai saldoista.
Viitteet
- Whitten, Davis, Peck & Stanley. (2008). Kemia. (8. ed.-A. Cengage -oppiminen.
- Wikipedia. (2020). Clausius-clapeyron-suhde. Haettu: vuonna.Wikipedia.org
- San José State University. (S.F.-A. Clausius-Clapeyron-yhtälö:
STIS -johdannainen ja soveltaminen meteorologiassa. Palautettu: SJSU.Edu - Bodner -ryhmä. (S.F.-A. Clausius-Clapeyron-yhtälö. Haettu: Chemed.Kemia.Purduke.Edu
- Chieh c. & Censulo A. (18. toukokuuta 2020). Clausius-Clapeyron-yhtälö. Kemian librettexts. Palautettu: Chem.Librettexts.org
- Walter J. Moore. (1962). Fysikaalinen kemia. (Neljäs painos). Longmanit.

