Toisen asteen yhtälöiden kaava, kuinka ratkaista ne, esimerkkejä, harjoituksia
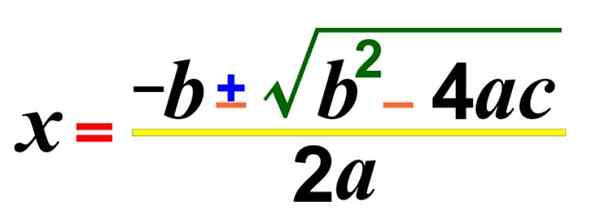
- 3618
- 118
- Arthur Terry II
Se Toisen asteen tai neliömäiset yhtälöt Ja tuntemattomalla on muoto kirves2 + BX + C = 0. Jos ≠ 0, koska 0 on 0, yhtälö muutetaan lineaariseksi yhtälöksi, ja kertoimet A, B ja C ovat todellisia lukuja.
Määritettävä tuntematon on x: n arvo. Esimerkiksi 3x -yhtälö2 - 5x + 2 = 0 on täydellinen toisen asteen yhtälö.
 Kuvio 1. Kaava tuntemattoman toisen asteen tai neliömäisen yhtälön ratkaisemiseksi
Kuvio 1. Kaava tuntemattoman toisen asteen tai neliömäisen yhtälön ratkaisemiseksi On myös variantteja, jotka tunnetaan epätäydellisinä toisen asteen yhtälöinä, joilla ei ole mitään termejä, paitsi kirves2. Tässä on joitain esimerkkejä:
x2 - 25 = 0
3x2 - 5x = 0
Al Juarismi, kuuluisa antiikin arabimatemaatikko, joka on kuvattu teoksissaan erityyppisiä ensimmäisen ja toisen asteen yhtälöitä, mutta vain positiivisilla kertoimilla. Se oli kuitenkin ranskalainen matemaattinen Päättäväinen-
Tämä on yleinen kaava, joka mahdollistaa neliömäisen yhtälön ratkaisemisen, sen löytämisen juuret tai nollat, vaikka ratkaisut eivät olisi todellisia. On myös muita tapoja ratkaista ne.
[TOC]
Kuinka ratkaista toisen luokan yhtälöt?
Toisen asteen yhtälöt voidaan ratkaista edellä annetulla kaavalla, ja on myös muita algebrallisia menettelytapoja, jotka voivat toimia joissain yhtälöissä.
Aiomme ratkaista ehdotetun yhtälön alussa kaavalla, joka on kelvollinen menetelmä mille tahansa toisen asteen yhtälölle tuntemattomilla:
3x2 - 5x + 2 = 0
Kaavan käyttämiseksi huomaamme oikein, että:
- -lla Se on termin kerroin x: llä2
- b - Se on lineaarisen termin kerroin
- c on riippumaton termi.
Tunnistetaan ne samasta yhtälöstä:
A = 3
B = -5
C = 2
Huomaa, että kertoimeen liittyvä merkki on otettava huomioon. Nyt korvaamme nämä arvot kaavassa:
Laskinnassa on symboli "enemmän - vähemmän" ±, mikä osoittaa, että juuren määrää voidaan pitää positiivisena ja myös negatiivisena. Toisen asteen yhtälöllä on korkeintaan kaksi todellista ratkaisua, ja tämä symboli ottaa sen huomioon.
Soitataan x1 ja x2 Näihin kahteen ratkaisuun: Sitten:
x1 = (5+1) / 6 = 1
x2 = (5-1)/6 = 4/6 = 2/3
Resoluutio tekijäksi
Jotkut toisen asteen yhtälöt koostuvat trinomeista, jotka ovat helposti tekijöitä. Jos näin on, tämä menetelmä on paljon nopeampi. Harkitse yhtälöä:
x2 + 7x - 18 = 0
Tekijä on tämä muoto:
Voi palvella sinua: Yhteydet: Yhteydet hahmot, kriteerit, esimerkit, harjoitukset(x +) ⋅ (x -)
Tyhjät tilat täytetään kahdella numerolla, jotka kerrotaan 18: ssa ja kun ne vähennetään, 7 on 7. Suluissa olevat merkit valitaan tällä kriteerillä:
-Ensimmäisessä suluissa ensimmäisen ja toisen termin välinen merkki on sijoitettu.
-Ja toisessa sulkussa on näkyvien merkkien tuote.
Mitä tulee numeroihin, ne ovat tässä tapauksessa helposti: ne ovat 9 ja 2. Vanhin sijoitetaan aina ensimmäiseen suluun, kuten tämä:
x2 + 7x - 18 = (x + 9). (x - 2)
Lukija voi tarkistaa jakautuvan ominaisuuden kautta, joka kehitettäessä tasa -arvon oikeanpuoleista tuotetta saadaan vasemmanpuoleinen. Nyt yhtälö kirjoitetaan uudelleen:
(x + 9) ⋅ (x - 2) = 0
Tasa -arvon toteuttamiseksi riittää, että toinen kahdesta tekijästä on nolla. Joten ensimmäisessä se on tehtävä1 = -9 tai voi olla, että toinen tekijä peruutetaan siinä tapauksessa X2 = 2. Nämä ovat yhtälöratkaisuja.
Graafinen menetelmä
Toisen asteen yhtälön juuret tai ratkaisut vastaavat vertauksen y = = kirves2 + bx + c Vaakasuoran akselin tai x -akselin kanssa. Niin että kuvaamalla vastaava vertaus löydämme toisen asteen yhtälön ratkaisun tekemällä y = 0.
Vaaka -akselin vertausten leikkaukset edustavat yhtälön ratkaisuja kirves2 + BX + C = 0. Vaaka -akselin vain leikkaa vain yksipisteessä olevassa juuressa on yksi juuri ja tämä on aina parabolin kärki.
Ja lopuksi, jos vertaus ei leikkaa vaaka -akselia, vastaava yhtälö kirves2 + BX + C = 0 Siitä puuttuu todellisia ratkaisuja.
Käsikaavion rakentaminen voi olla työlästä, mutta ohjelmien avulla, jotka kuvaavat verkossa, se on hyvin yksinkertaista.
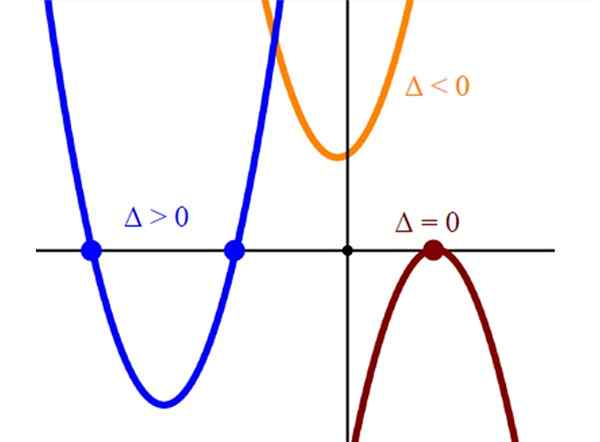 Kuva 2. Kolmen tyyppisten vertausten graafinen esitys, jossa on kaksi, yksi ja ei risteystä vaakasuoran akselin kanssa. Lähde: Wikimedia Commons.
Kuva 2. Kolmen tyyppisten vertausten graafinen esitys, jossa on kaksi, yksi ja ei risteystä vaakasuoran akselin kanssa. Lähde: Wikimedia Commons. Resoluutio tieteellisellä laskurilla
Monilla tieteellisten laskimien malleilla on mahdollisuus ratkaista toisen asteen yhtälöt (ja myös muun tyyppiset yhtälöt). Tietämään se sinun on tarkistettava valikko.
Kun tuntemattoman neliömäinen yhtälövaihtoehto on valittu, valikossa pyydetään syöttämään kertoimien A, B ja C arvot ja palauttaa todelliset ratkaisut, jos niitä on. Ja on myös malleja tieteellisistä laskimista, jotka työskentelevät monimutkaisten lukujen kanssa ja tarjoavat nämä ratkaisut.
Voi palvella sinua: 2: 2: MIKSI JA SELLITTELYErottelu toisen asteen yhtälöstä
Syrjinnän määritelmä määritellään neliöjuuren alla olevaksi, onko yhtälöllä todellisia ratkaisuja vai ei, ja kuinka monta on, ilman tarvetta ratkaista ensin:
Δ = b2 - 4AC
Syrjivän merkin mukaan tiedetään, kuinka monta ratkaisua yhtälöllä on tämän kriteerin mukaan:
-Kaksi todellista ratkaisua: Δ> 0
-Todellinen ratkaisu (tai kaksi identtistä ratkaisua): Δ = 0
-Ei oikeaa ratkaisua: δ < 0
Esimerkiksi kuinka monta ratkaisua toisen asteen yhtälöllä on -7x2 +12x + 64 = 0? Tunnistamme kertoimet:
A = -7
B = 12
C = 64
Δ = b2 - 4ac = 122 - 4x (-7) x 64 = 144 + 1792 = 1936> 0
Yhtälöllä on kaksi ratkaisua. Katsotaanpa tätä:
x2 - 6x + 9 = 0
A = 1
B = -6
C = 9
Δ = (-6)2 - 4 x 1 x 9 = 36 - 36 = 0
Tämä on yhtälö, jolla on ainutlaatuinen ratkaisu tai kaksi yhtä suurta ratkaisua.
Esimerkkejä yksinkertaisista toisen asteen yhtälöistä
Alussa sanoimme, että toisen asteen yhtälöt voivat olla täydellisiä, jos trinomiaalinen on, ja epätäydellinen, jos lineaarinen termi tai riippumaton termi puuttui. Katsotaanpa nyt joitain tiettyjä tyyppejä:
X -muotoyhtälö2 + mx + n = 0
Tässä tapauksessa A = 1 ja kaava pienennetään:
Tämän tyyppiselle yhtälölle ja aina jäljellä olevista kertoimista riippuen tekijämenetelmä voi toimia hyvin, kuten edellisessä osassa näimme.
AX -muodon epätäydellinen yhtälö2 + C = 0
Ratkaisu, jos se on olemassa, on muoto:
On todellinen ratkaisu, kun O C: llä on negatiivinen merkki, mutta jos kahdella termillä on sama merkki, ratkaisu on kuvitteellinen.
AX -muodon epätäydellinen yhtälö2 + BX = 0
Tämä yhtälö ratkaistaan nopeasti käyttämällä tekijää, koska x on yleinen tekijä molemmissa termeissä. Yksi ratkaisuista on aina x = 0, toinen on tällainen:
kirves2 + BX = 0
x (ax + b) = 0
AX + B = 0 → x = -b/a
Katsotaanpa sitten esimerkkiä. Ratkaista:
x2 - 5x = 0
x (x - 5) = 0
Siksi x1 = 0 ja x2 = 5
Yhtälöt nimittäjän kanssa
On olemassa useita rationaalisia yhtälöitä, joissa tuntematonta voi olla läsnä sekä numeraattorissa että nimittäjässä tai jopa vain jälkimmäisessä, ja että algebrallisilla manipulaatioilla pelkistetään kvadraattisiin yhtälöihin.
Tapa ratkaista ne on kertoa tasa -arvon molemmat puolet vähimmäisvaatimuksella tai m.c.M nimittäjien m ja sitten uudelleen ehdot. Esimerkiksi:
Voi palvella sinua: kuinka monta halkaisijaa kehällä on?Korkeamman asteen yhtälöt, jotka on muunnettu neliömäiseksi
On olemassa korkeamman asteen yhtälöitä, jotka muuttuvan muutoksen avulla voidaan ratkaista ikään kuin ne olisivat neliömäisiä, esimerkiksi tämä yhtälö Bikadrada-
x4 - 10x2 + 9 = 0
Antaa x2 = U, sitten yhtälö muutetaan:
tai2 - 10U + 9 = 0
Tämä yhtälö ratkaistaan nopeasti tekijällä, löytämällä kaksi lukua, jotka kerrottuivat 9: ssä ja lisätty 10. Nämä numerot ovat 9 ja 1:
(U - 9).(U - 1) = 0
Siksi tämän yhtälön ratkaisut ovat u1 = 9 ja u2 = 1. Palaamme nyt muutoksen:
x2 = 9 → X1 = 3 ja x2 = -3
x2 = 1 → x1 = 1 ja x2 = -1
Alkuperäinen yhtälö on järjestyksessä 4, joten siinä on vähintään 4 juuria. Esimerkki on -3, -1, 1 ja 3.
Yksinkertaiset ratkaisut
- Harjoitus 1
Ratkaise seuraava neliömäinen yhtälö tuntemattoman kanssa nimittäjässä:
Pienin yleinen moninkertainen on x (x+2) ja sen on kerrottava kaikkiin termeihin:
Vastaava lauseke pysyy:
5x (x+2) - x = x (x+2)
Kehitämme:
5x2 + 10x - x = x2 + 2x
Kaikki termit siirretään tasa -arvon vasemmalle ja oikealle on vasemmalle 0:
5x2 + 10x - x - x2 - 2x = 0
4x2 - 7x = 0
Vaikutamme, koska se on epätäydellinen yhtälö:
x (4x - 7) = 0
Yksi ratkaisuista on x = 0, toinen on:
4x = 7
x = 7/4
- Harjoitus 2
Etsi toisen asteen yhtälöiden ratkaisu:
a) -7x2 +12x + 64 = 0
b) x2 - 6x + 9 = 0
Liittää jhk
Tästä yhtälöstä tiedämme Δ -determinantin, koska se laskettiin esimerkkinä aiemmin, joten aiomme hyödyntää sitä, ilmaisemalla liuotinkaavan seuraavasti:
x1 = (-12+44)/ - 14 = - (32/14) = - (16/7)
x2 = (-12 -44) / -14 = 4
Ratkaisu b
Neliömäinen trinomiaalinen x2 - 6x + 9 on tekijä, koska se on täydellinen neliömäinen trinomi:
x2 - 6x + 9 = (x-3)2 = 0
Tämän yhtälön ratkaisu on x = 3.
- Harjoitus 3
Mikä on yhtälö, jonka ratkaisut ovat 3 ja 4?
Ratkaisu
Fakoroitu ekspressio on:
(x - 3) ⋅ (x - 4) = 0
Jakavan omaisuuden soveltaminen:
x2 - 4x -3x + 12 = 0
Kaksi keskeistä termiä ovat samanlaisia ja niitä voidaan vähentää, koska se on: Lähtö:
x2 - 7x + 12 = 0
Viitteet
- Kalju. 1977. Perusalgebra. Venezuelan kulttuuriversiot.
- Hoffman, J. Matematiikan aiheiden valinta. Nide 2.
- Jiménez, r. 2008. Algebra. Prentice Hall.
- Stewart, J. 2006. Precculment: Laskentamatematiikka. Viides. Painos. Cengage -oppiminen.
- Zapata, f. 4 tapaa ratkaista toisen asteen yhtälö. Toipunut: Francesphysics.Blogin.com.
- Zill, D. 1984. Algebra ja trigonometria. McGraw Hill.
- « Lisäyspolymeerien rakenne, ominaisuudet, toiminto, käyttö
- Luontaiset motivaatioominaisuudet ja esimerkit »



\pm&space;\sqrt(-5)^2-4\times&space;3\times&space;22\times&space;3=)

^2-4c2)


x-\fracx(x+2)x+2=x(x+2))
=\frac-12\pm&space;44-14)