Vektorin elementit

Se Vektorin elementit Ne ovat osoite, etäisyys ja moduuli. Matematiikassa, fysiikassa ja tekniikassa vektori on geometrinen esine, jolla on suuruus (tai pituus) ja suunta. Vektorialgebran mukaan vektoreita voidaan lisätä muihin vektoreihin.

Usein vektoria edustaa linjasegmentti, jolla on määritelty osoite, tai se on graafisesti esitetty nuolena, yhdistämällä alkupiste päätelaitteeseen B pisteeseen, merkitty AB: llä.

Vektori on mitä tarvitaan pisteeseen B kohtaan B. Vektoreilla on tärkeä rooli fysiikassa: liikkuvan esineen nopeus ja kiihtyminen ja siinä olevat voimat voidaan kuvata vektoreilla.

Monia muita fyysisiä ominaisuuksia voidaan ajatella vektoreiksi. Fyysisen vektorin matemaattinen esitys riippuu sen kuvaamisesta käytetystä koordinaattijärjestelmästä.

Vektoreita on monenlaisia, muun muassa löydämme liukuvektorit, kolineaalivektorit, samanaikaiset vektorit, sijaintivektorit, vapaat vektorit, rinnakkaisvektorit ja koplanaresvektorit, muun muassa.

Vektorin elementit

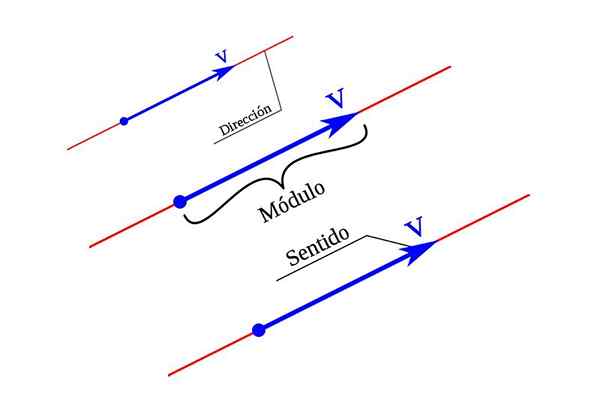
Pääasiassa vektorilla on kolme elementtiä: suunta, merkitys ja moduuli.

Osoite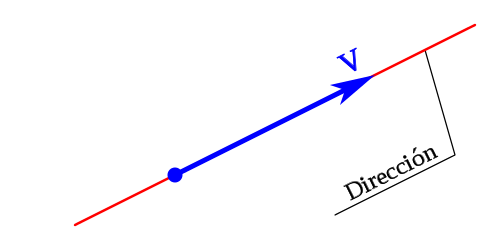

Vektori on kokonaisuus, jolla on suuruus ja suunta. Esimerkkejä vektoreista ovat siirtymä, nopeus, kiihtyvyys ja lujuus. Yksi näistä vektorimääristä kuvata on välttämätöntä löytää suuruus ja suunta.

Esimerkiksi, jos objektin nopeus on 25 metriä sekunnissa, objektin nopeuden kuvaus on epätäydellinen, koska esine voi liikkua 25 metriä sekunnissa etelään tai 25 metriä sekunnissa pohjoiseen, tai tai pohjoiseen 25 metriä sekunnissa kaakkoon.

Objektin nopeuden kuvaamiseksi molemmat on määriteltävä: molemmat 25 metrin sekunnissa että suunta, esimerkiksi etelään.

Jotta vektorimäärien kuvaukset olisivat hyödyllisiä, on tärkeää, että kaikki saavuttavat sopimuksen objektinhallinnan kuvaamisesta.

Useimmat ihmiset ovat tottuneet ajatukseen, että suunta viitataan toiseen, jos katsot oikealle. Mutta tämä on pelkkä yleissopimus, jota Map -elokuvantekijät ovat käyttäneet vuosia, jotta kaikki voivat sopia.

Joten mikä on vektorimäärän suunta, joka ei mene pohjoiseen tai itään, vaan jonnekin pohjoisen ja idän välillä? Näissä tapauksissa on tärkeää, että mainitun vektorin suunnan kuvaamiseksi on olemassa yleissopimus.

Tätä yleissopimusta kutsutaan CCW: ksi. Tätä yleissopimusta käyttämällä voimme kuvata minkä tahansa vektorin suunnan sen kiertokulman suhteen vasemmalle.

Tätä yleissopimusta käyttämällä Pohjoinen osasto olisi 90 °, koska jos vektori osoittaa itään, se on käännettävä 90 ° vasempaan suuntaan Pohjoispisteen saavuttamiseksi.

Samoin länsiosoite sijaitsee 180 °: ssa, koska länteen osoittavaa vektoria olisi käännettävä 180 ° vasemmalle osoittamaan länsipisteeseen.

Toisin sanoen vektorin suunta esitetään vektorissa olevan linjan tai minkä tahansa samansuuntaisen linjan kautta.

Se määritetään vektorin ja minkä tahansa muun vertailulinjan välillä muodostumalla kulmalla. Toisin sanoen vektorissa olevan viivan suunta tai sen yhdensuuntainen linja on vektorin suunta.

Aisti

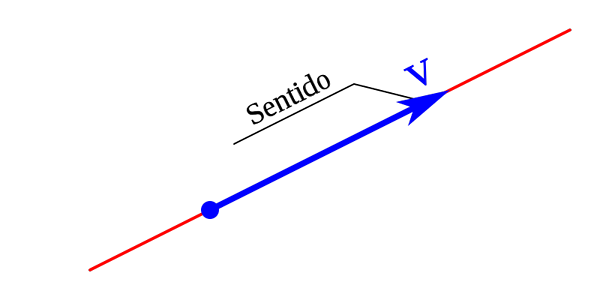
Vektorin suunta viittaa elementtiin, joka kuvaa kuinka kohta A menee loppuun B:

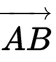
Vektorin suunta määritetään kahden pisteen luokkaa vektorin yhdensuuntaisella viivalla, toisin kuin vektorin suunta, joka määritetään vektorin ja minkä tahansa vertailulinjan ja/tai tason välisellä suhteella.

Sekä suunta että merkitys määrittävät vektorin suunnan. Suunta sanoo, mihin kulmaan vektori on, ja merkitys sanoo missä osoittaa.

Vektoriosoite määrittää vain kulman, jonka vektori suorittaa vaaka -akselillaan, mutta se voi luoda epäselvyyttä, koska nuoli voi osoittaa kahteen vastakkaiseen suuntaan ja yhtä suuri kuin sama kulma.

Merkitys selventää tätä epäselvyyttä ja osoittaa, mihin nuoli osoittaa tai missä vektori on suunnattu.

Jotenkin merkitys kertoo meille tilauksen, jossa vektori luetaan. Osoittaa, missä vektori päättyy ja missä vektori päättyy.

Moduuli

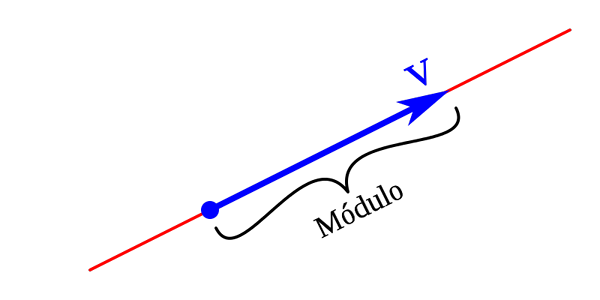
Moduuli tai vektorin amplitudi voidaan määritellä AB -segmentin pituudeksi. Moduuli voidaan edustaa pituudella, joka on verrannollinen vektorin arvoon. Vektorin moduuli on aina nolla tai muissa tapauksissa positiivinen luku.

Matematiikassa vektori määritellään sen euklidinen etäisyys (moduuli), suunta ja suunta.

Euklidinen etäisyys tai euklidinen etäisyys on 'tavallinen' etäisyys suorassa linjassa kahden pisteen välillä, jotka sijaitsevat euklidisessa tilassa. Tällä etäisyydellä euklidialaisesta tilasta tulee metrinen tila.

Euklidian etäisyys kahden pisteen välillä, esimerkiksi P ja Q, on etäisyys niihin yhdistävän linjasegmentin välillä:

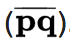
Pisteen sijainti euklidian avaruudessa n on vektori. Siten p ja q ovat vektoreita, alkaen tilan alkuperästä ja sen kärjet, jotka osoittavat kaksi pistettä.

Euklidinen standardi, suuruus tai euklidinen etäisyys vektorista mittaa mainitun vektorin pituuden.

Viitteet

1. Suuntavektori. Palautettu fysiikkakurssihuoneesta.com.
2. Mikä on vektorin tunne? Fysiikasta toipunut.Stackexchange.com.