Enegon -ominaisuudet, miten tehdä enegon, esimerkkejä

Eräs Engon Se on yhdeksän sivun ja yhdeksän kärjen monikulmio, joka voi olla säännöllinen tai ei. Engonin uskonto tulee kreikasta ja koostuu kreikkalaisista sanoista Ennea (yhdeksän ja Gonon (kulma).

Vaihtoehtoinen nimi yhdeksän puolella olevalle monikulmiolle on ei -sanallinen sana, joka tulee latinaksi ei - (yhdeksän ja Gonon (Vertex). Toisaalta, jos enegonin sivut tai kulmat ovat epätasa -arvoisia toisiinsa, siellä on sitten a epäsäännöllinen engon. Jos päinvastoin, engonin yhdeksän puolta ja yhdeksän kulmaa ovat yhtä suuret, niin se on säännöllinen Enegon.

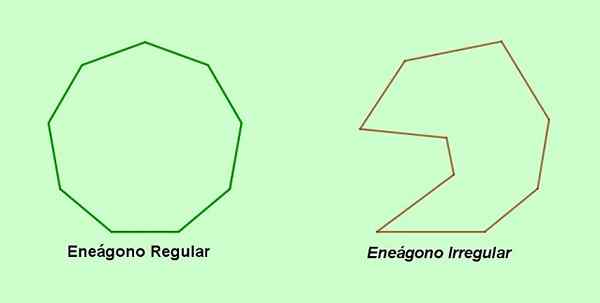
Kuvio 1. Säännöllinen engon ja epäsäännöllinen engon. (Oma yksityiskohta)

[TOC]

Enegon -ominaisuudet

N -puolien monikulmion kohdalla sen sisäkulmien summa on:

(N - 2) * 180º

Engonissa se olisi n = 9, joten sen sisäkulmien summa on:

SA = (9 - 2) * 180º = 7 * 180º = 1260º

Missä tahansa monikulmiossa diagonaalien lukumäärä on:

D = n (n - 3) / 2 ja Enegonin tapauksessa, kuten n = 9, sinun on d = 27.

Säännöllinen Enegon

Enegonissa tai tavallisessa Nonagonissa.

Sitten on tarpeen mitata engonin sisäkulmat ovat 1260º / 9 = 140º.

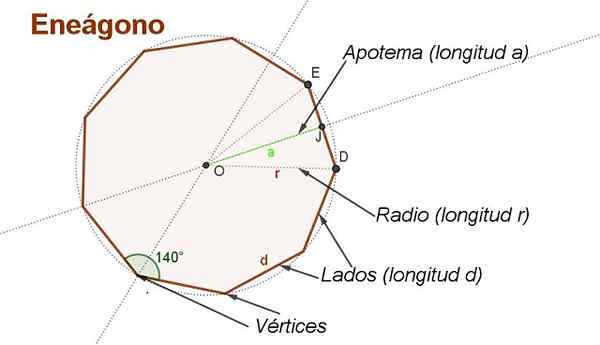Kuva 2. Apootemi, radio, sivut, kulmat ja säännölliset engonin kärkipisteet. (Oma yksityiskohta)

Päätelemään tavallisen engonin alueen kaava sivulla d -d On kätevää tehdä joitain apurakenteita, kuten kuvassa 2 esitetyt.

Keskus on JOMPIKUMPI Kahden vierekkäisen sivun välitalojen piirtäminen. Keskusta JOMPIKUMPI Kärjessä.

Pituuden säde r - Segmentti menee keskustasta JOMPIKUMPI Engonin kärkipaikassa. Radiot on esitetty kuvassa 2 Od ja OE pitkä r -.

Voi palvella sinua: Symmetria

Apotemi on segmentti, joka kulkee keskustasta keskipisteeseen Enegonin toisella puolella. Esimerkiksi Oman Se on apotemi, jonka pituus on -lla.

Enegonin tunnettu puolen ja apothemin alue

Tarkastelemme kolmiota OODI Kuviosta 2. Tämän kolmion alue on sen pohjan tuote - korkeudella Oman jaettuna 2:

Alue OODI = (From * OJ) / 2 = (D * a) / 2

Koska Enegonissa on saman alueen 9 kolmiota, päättyy silloin, että saman pinta -ala on:

Engonin alue = (9/2) (d * a)

Tunnetun engonin pinta -ala

Jos vain Engonin pituus tunnetaan, on välttämätöntä löytää apotemin pituus, jotta voidaan käyttää edellisen osan kaavaa,.

Tarkastelemme kolmiota Kisko Suorita J - (Katso kuva 2). Jos vääntömomentin trigonometristä suhdetta sovelletaan, se saadaan:

niin(∡Oej) = Oman - Esim.

Kulma ∡oej = 140º / 2 = 70º, EO Enegonin sisäkulman puolustaja.

sitä paitsi, Oman Se on pituuden apotemi -lla.

Sitten J - Se on keskipiste Ed Seuraa, että Ex = d/2.

Edellä olevien arvojen korvaaminen tangentin suhteessa on:

Tan (70º) = A / (d / 2).

Nyt puhdistamme apoteemin pituuden:

A = (d/2) Tan (70º).

Aikaisempi tulos korvataan alueen kaavassa saadaksesi:

Engonin alue = (9/2) (d * a) = (9/2)( D * (d/2) Rusketus (70º))

Lopuksi on kaava, joka mahdollistaa tavallisen Enegon -alueen saamisen, jos vain pituus tunnetaan d -d sen sivuista:

Engonin alue = (9/4) d² Tan (70º) = 6 1818 d²

Tavallisen engonin kehä tunsi sen sivun

Monikulmion kehä on sen sivujen summa. Enegonin tapauksessa, kuten jokainen sivu, se mittaa pituuden d -d, Sen kehä on yhdeksän kertaa summa d -d, tarkoittaen:

Voi palvella sinua: polynomiyhtälöt

Kehä = 9 d

Engonin kehä tunsi radionsa

Kolmion huomioon ottaminen Kisko Suorita J - (Katso kuva 2), Kosenia käytetään trigonometristä syytä:

cos (∡Oej) = Esim - OE = (d / 2) / r

Mistä olet hankkinut:

D = 2r cos (70º)

Korvaamalla tämän tuloksen, kehäkaava saadaan engonin säteen funktiona:

Kehä = 9 d = 18 r cos (70º) = 6 1564 r

Kuinka tehdä tavallinen engon

1- Säännöllisen enegonin rakentamiseksi, säännön ja kompassin kanssa, se perustuu kehään c joka rajoittaa Enegonia. (Katso kuva 3)

2- Kaksi kohtisuoraa viivaa piirretään keskustan tai ympärysmiipan läpi. Sitten yhden linjan risteykset A ja B on merkitty kehällä.

3- Kompassilla, joka tekee keskuksen sieppauksessa B ja aukko, joka on yhtä suuri kuin säde bo.

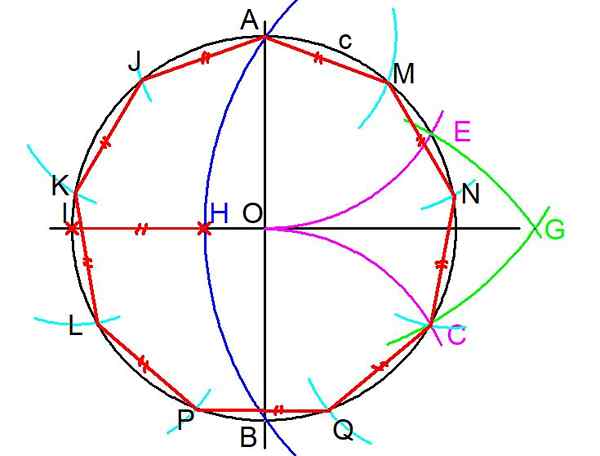Kuva 3. Vaiheet tavallisen engonin rakentamiseksi. (Oma yksityiskohta)

4- Edellinen vaihe toistetaan, mutta keskusta A- ja radio-AO-kaari on piirretty, joka sieppaa kehälle c pisteessä E.

5- AC-aukko ja keskusta A-kehän kaaressa vedetään. Samoin avaamisen kanssa ja keskusta B vedetään toinen kaari. Näiden kahden kaaren leikkauspiste on merkitty G: ksi.

6- valmistuskeskus G: ssä ja GA: n avautuessa kaaren piirretään, joka sieppaa toissijaisen akselin (tässä tapauksessa vaakasuora) pisteessä H. Toissijaisen akselin leikkauspiste on merkitty alkuperäisellä kehällä c kuten i.

7- IH-segmentin pituus on yhtä suuri kuin Engonin sivulla oleva pituus D.

8- Kompassin avaamisella ih = D keskikarkot vedetään peräkkäin Radio AJ: lle, Centro J Radio AK, KL Radio KL ja Centro L Radio LP.

Se voi palvella sinua: lineaariset muunnokset: Ominaisuudet, mitkä ovat käyttö, tyypit, esimerkit

9- Samoin alkaen A: sta ja oikealta puolelta, radioarcos ih = D on piirretty alkuperäiseen kehälle C-pisteet M, N, C ja Q.

10- Lopuksi segmentit AJ, JK, KL, LP, AM, MN, NC, CQ ja Lopulta PB piirretään.

On huomattava, että rakennusmenetelmä ei ole täysin tarkka, koska voidaan varmistaa, että viimeinen PB -puoli on 0,7% pidempi kuin toiset puolet. Tähän päivään mennessä rakennus- ja kompassin rakennusmenetelmää ei tiedetä, mikä on 100% tarkka.

Esimerkit

Joitakin ratkaistuja esimerkkejä käsitellään alla.

Esimerkki 1

Haluat rakentaa tavallisen engonin, jonka sivut mittaavat 2 cm. Minkä radion tulisi ympärysmittaa, jota se on, joten aikaisemmin kuvattua rakennetta sovellettaessa haluttu tulos saadaan?

Ratkaisu:

Aikaisemmassa osassa johdettiin kaava, joka liittyy rajoitetun ympärysmittan säteen R: n säteen R: n kanssa:

D = 2r cos (70º)

R: n puhdistaminen edellisestä ilmaisusta, joka meillä on:

R = d / (2 cos (70º)) = 1 4619 * d

Arvon D = 2 cm korvaaminen edellisessä kaavassa saadaan 2,92 cm: n säde.

Esimerkki 2

Paljon?

Ratkaisu:

Vastaamaan tähän kysymykseen sinun on viitattava aiemmin osoitettuun kaavaan, jonka avulla voit löytää enegonin alueen, joka tunnetaan sen puolella d:

Engonin alue = (9/4) d² Tan (70º) = 6 1818 d²

Korvataan d sen arvon 2 cm etukaavassa saadaan:

Engonin alue = 24,72 cm

Viitteet

1. C. JA. -Lla. (2003). Geometriaelementit: harjoituksilla ja kompassin geometrialla. Medellinin yliopisto.
2. Campos, f., Cerecedo, f. J -. (2014). Matematiikka 2. Patria -toimitusryhmä.
3. Vapautettu, k. (2007). Tutustu monikulmioihin. Vertailuindeksiyhtiö.
4. Hendrik, V. (2013). Yleiset monikulmiot. Birkhäuser.
5. Iger. (S.F.-A. Matematiikka ensimmäisen lukukauden Tacaná. Iger.
6. Jr. Geometria. (2014). Monikulmio. Lulu Press, Inc.
7. Miller, Heeren ja Hornsby. (2006). Matematiikka: Perustelu ja sovellukset (kymmenes painos). Pearson -koulutus.
8. Patiño, m. (2006). Matematiikka 5. Toimitusohjelma.