Gravitaatioenergiakaavat, ominaisuudet, sovellukset, harjoitukset

Se Gravitaatioenergia Se on massiivinen esine, kun se on upotettu toisen tuottamaan gravitaatiokenttään. Joitakin esimerkkejä esineistä, joilla on painovoima energiaa.

Isaac Newton (1642-1727) ymmärsi ensimmäisenä, että painovoima on universaali ilmiö ja että jokainen massatuoteinen esine tuottaa ympäristössään kentän, joka pystyy tuottamaan yhden voiman toiseen.

Kuvio 1. Kuulla kiertävällä maalla on gravitaatioenergia. Lähde: Pixabay

[TOC]

Kaavat ja yhtälöt

Newtonissa mainittu voima tunnetaan gravitaatiovoimana ja se tarjoaa energiaa esineelle, jolla se toimii. Newton muotoili yleismaailmallisen gravitaatiolain seuraavasti:

"Ole vastaavasti kaksi erityistä massaobjektia M1 ja M2, joista kukin kohdistaa toisella vetovoiman, joka on verrannollinen heidän massojensa tuotteeseen ja käänteisesti verrannollinen ne erottivat etäisyyden neliöön.".

Edellisessä ilmaisussa, F Objekti 1 kohdistaa objektiin 2 (tai päinvastoin), että objekti 1 on painovoiman voima (tai päinvastoin, M1 ja m2 Objektien vastaavat massat ja R on etäisyys, joka erottaa esineet. G Se on vakio suhteellisuus, jota kutsutaan gravitaatiovakioksi.

Gravitaatioenergia TAI liittyy painovoimavoimaan F On:

Huomaa negatiivisen merkin läsnäolo, mikä tarkoittaa, että jos esineiden välinen ero on rajallinen, sen painovoima on negatiivinen. Mutta jos erottelu pyrkii äärettömyyteen, gravitaatioenergia on nolla.

Gravitaatiokenttään upotettu esineellä on gravitaatiopotentiaalienergia TAI ja kineettinen energia K -k -. Jos muita vuorovaikutuksia ei ole tai ne ovat vähäisiä voimakkuuksia, kokonaisenergia JA Tämän esineen on sen gravitaatioenergian summa plus sen kineettinen energia:

E = k + u

Jos esine on painovoimakentällä ja muita hajoavia voimia ei ole, kuten kitka tai ilmankestävyys, niin kokonaisenergia JA Se on määrä, joka pysyy vakiona liikkeen aikana.

Gravitaatioenergian ominaisuudet

- Esineellä on gravitaatiopotentiaalienergia, jos se on vain toisen tuottaman gravitaatiokentän läsnäollessa.

- Kahden esineen välinen gravitaatioenergia kasvaa, koska niiden välinen etäisyys on suurempi.

- Gravitaatiovoiman tekemä työ on tasa -arvoinen ja vastoin lopullisen aseman gravitaatioenergian vaihtelua sen alkuperäisen sijainnin suhteen.

Se voi palvella sinua: mikä on hiukkasen tasapaino? (Esimerkkejä)

- Jos runko altistetaan vain painovoiman vaikutuksesta, sen gravitaatioenergian variaatio on yhtä suuri ja vastoin sen kineettisen energian vaihtelua.

- Massaobjektin potentiaalinen energia m korkeudella h Maan pinnan suhteen Mgh kertaa suurempi kuin pinnan potentiaalinen energia, oleminen g painovoiman kiihtyvyys korkeuksiin h Paljon alhaisempi kuin maanpäällinen säde.

Kenttä- ja painovoimapotentiaali

Gravitaatiokenttä g Se määritellään painovoimana F massayksikköä kohti. Se määritetään asettamalla testihiukkas jokaiseen avaruuden pisteeseen ja laskemalla osamäärä testihiukkasiin kohdistuvan voiman välillä jaettuna sen massan arvolla:

g = F / m

Massaobjektin M painovoimapotentiaali V, koska kyseisen esineen gravitaatiopotentiaalienergia on jaettuna sen omalla massalla.

Tämän määritelmän etuna on, että gravitaatiopotentiaali riippuu vain gravitaatiokentästä, joten kun potentiaali on tiedossa V, Gravitaatioenergia TAI massaobjekti m On:

U = m.V 

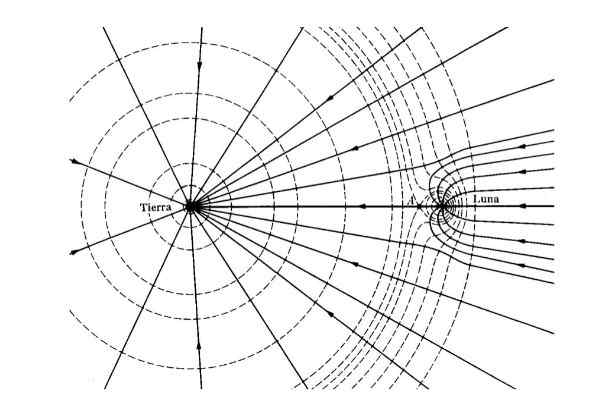Kuva 2. Gravitaatiokenttä (jatkuvat viivat) ja Equi -potentiaalinen (segmentoitu viiva) Maa -Luna -järjestelmälle. Lähde: W T Scott, AM. J -. Fyysinen. 33, (1965).

Sovellukset

Gravitaatiopotentiaalienergia on mitä kehot varastoivat, kun ne ovat painovoimakentällä.

Esimerkiksi säiliön sisältävällä vedellä on enemmän energiaa siinä määrin, että säiliö on korkeampi.

Suuremmassa säiliössä, sitä suurempi vesipistorasian nopeus hanalla. Tämä johtuu siitä, että veden potentiaalinen energia säiliön korkeudella muuttuu kineettiseksi vesienergiaksi hanan poistumisessa.

Kun vesi on vaurioitunut vuoren yläosassa, tätä potentiaalista energiaa voidaan käyttää sähköntuotantoturbiinien kiertämiseen.

Gravitaatioenergia selittää myös vuorovedet. Kun energia ja painovoima riippuvat etäisyydestä, kuun painovoima veto on suurempi kuuta lähinnä olevan maan edessä kuin kauimpana ja vastakkaisimmassa kasvossa.

Tämä tuottaa eron voimissa, jotka muodostuvat merenpinnan. Vaikutus on suurempi uuteen kuuhun, kun aurinko ja kuu ovat linjassa.

Mahdollisuus rakentaa spatiaalisia ja satelliittiasemia, jotka pysyvät suhteellisen lähellä planeettamme, johtuu maapallon tuottamasta gravitaatioenergiasta. Ellei avaruusasemat ja keinotekoiset satelliitit vaeltavat avaruuden läpi.

Se voi palvella sinua: IMANTANTION: Mikä koostuu, menetelmä ja esimerkit

Maapallon gravitaatiopotentiaali

Oletetaan, että maapallolla on massa M ja esine, joka on maanpinnan yläpuolella etäisyydellä r - Saman keskuksen suhteen on massa m. 

Tässä tapauksessa gravitaatiopotentiaali määritetään gravitaatioenergiasta, joka jakautuu yksinkertaisesti esineen massan välillä:

Maan pinnan painovoimapotentiaali saadaan korvaamalla r - Maanpäällisen säteen r_T. 

Potentiaalienergia lähellä maan pintaa

Oletetaan, että maapallolla on radio R -_T  ja massa M.

Vaikka maa ei olisi oikea -aikainen esine, sen pinnalla oleva kenttä vastaa sitä, mikä saadaan, jos kaikki sen massa M Se keskittyi keskustaan ​​siten, että esineen gravitaatioenergia korkeudella h maan pinnalla on 

U (r_T + h) = -G.M m (r_T + H)^-1

Mutta koska h on paljon vähemmän kuin r_T, Aikaisempi ilmaisu voi lähestyä 

U = uo + mgh

Missä g on painovoiman kiihtyvyys, jonka keskiarvo maan alueella on 9.81 m/s^2.

Sitten massa M: n potentiaalienergia EP maan pinnan korkeudella H: on:

EP (H) = U +UO = MGH

Maan pinnalla H = 0, joten pinnalla olevalla esineellä on EP = 0. Yksityiskohtaiset laskelmat voidaan nähdä kuvasta 3.

Kuva 3. Gravitaatiopotentiaalienergia korkeudella h pinnalla. Lähde: valmistettu f. Zapata.

Harjoitukset 

Harjoitus 1: Gravitaatio maan romahtaminen

Oletetaan, että planeettamme kärsii painovoiman romahtamisesta lämpöenergian menettämiseksi sisällä ja sen säde hajoaa jopa puolet nykyisestä arvosta, mutta planeetan massa on vakio.

Määritä, mikä olisi painovoiman kiihtyvyys uuden maan pinnan lähellä ja kuinka paljon 50 kg-F: tä painava selviytyjä ennen romahtamista. Lisää tai vähentää ihmisen painovoimaa ja missä tekijässä.

Ratkaisu

Painovoiman kiihtyvyys planeetan pinnalla riippuu sen massasta ja säteestä. Gravitaatiovakio on universaali ja palvelee yhtäläisesti planeettoja ja eksoplaneettoja.

Jos meidät nostetaan, jos maan sädettä vähenee puoleen, uuden maan vakavuuski. Yksityiskohdat näkyvät seuraavassa taulussa.

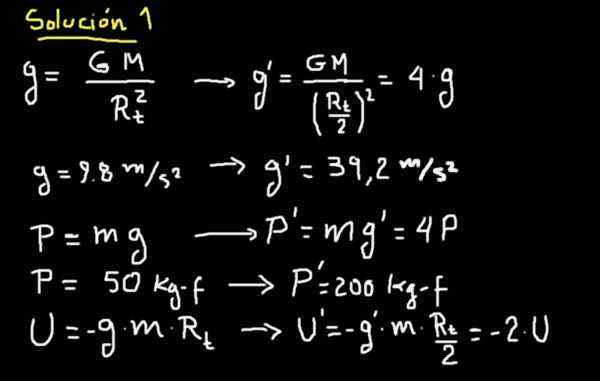
Tämä tarkoittaa, että supermies ja selviytyjä, että vanhassa planeetalla painoi 50 kg-F: n painaa 200 kg-F uudella planeetalla.

Voi palvella sinua: Lämpötasapaino: Yhtälöt, sovellukset, harjoitukset

Toisaalta gravitaatioenergia on vähentynyt puoleen uuden planeetan pinnalla.

Harjoitus 2: Gravitaation romahtaminen ja paeta nopeus

Harjoitteluun 1 kerättyyn tilanteeseen viitaten, mikä tapahtuisi pakokaasun nopeudelle: kasvaa, vähenee, missä tekijässä?

Ratkaisu 2

Pakokaasunopeus on vähimmäisnopeus, joka on tarpeen planeetan painovoiman vetovoiman välttämiseksi.

Sen laskemiseksi oletetaan, että tällä nopeudella ampuu ammus saavuttaa äärettömyyden nollalla nopeudella. Lisäksi äärettömyydessä gravitaatioenergia on nolla. Siksi ammus, joka ampuu pakokaasun nopeudella, ei ole kokonaisenergiaa.

Toisin sanoen planeetan pinnalla ampumishetkellä ammuksen + gravitaatioenergian kineettisen energian summan on oltava tyhjä:

½ m ve^2 - (g m.Herra_T = 0

Huomaa, että pakokaasun nopeus ei riipu ammuksen taikinasta ja sen neliöarvo on

Ve^2 = (2 g m) / r_T

Jos planeetta romahtaa jopa säteen puolet alkuperäisestä, uuden pakokaasun nopeuden neliö tulee kaksinkertaiseksi.

Siksi uusi pakokaasunopeus kasvaa ja muuttuu 1.41 kertaa vanha poistumisnopeus:

Ve '= 1.41 Katso

Harjoitus 3: Applen gravitaatioenergia

Poika rakennuksen parvekkeella 30 metrin päässä maasta vapauttaa 250 g: n omenan, joka muutaman sekunnin kuluttua saavuttaa maahan.

Kuva 4. Omenan potentiaalinen energia muuttuu kineettiseksi energiaksi putoamisen aikana. Lähde: Pixabay.

a) Mikä on omenan yläosassa olevan omenan gravitaatioenergiaero maaperän tasolla?

b) Kuinka nopeasti omena juuri ennen leviämistä maahan?

c) Entä energia, kun omena on murskattu maahan? 

Ratkaisu

a) ero gravitaatioenergiassa on 

m.g.H = 0.250 kg * 9.81 m/s^2 * 30 m = 73.6 J

b) potentiaalienergia, joka omenalla oli, kun se oli 30 m korkea, muuttuu kineettiseksi energiaksi, kun omena saavuttaa maahan.

½ m v^2 = m.g.h

V^2 = 2.g.h

Korvaamalla arvot ja selvitys seuraa, että omena saavuttaa maan nopeudella 24.3 m/s = 87.3 km/h.

c) On selvää, että omena on hajallaan ja kaikki alussa kertyneet gravitaatioenergiat menetetään lämmön muodossa, koska omenakappaleet ja iskuvyöhyke lämmitetään, lisäksi osa energiasta häviää myös ääniaaltojen muodossa "Splash".

Viitteet

1. Alonso, m. (1970). Vol fysiikka. 1, Inter -American Educational Fund. 
2. Hewitt, Paul. 2012. Käsitteellinen fysiikka. Viides. Ed. Pearson.
3. Ritari, r. 2017. Tutkijoiden fysiikka ja tekniikka: strategialähestymistapa. Pearson.
4. Sears, f. (2009).University Physics Vol. 1 
5. Wikipedia. Gravitaatioenergia. Palautettu: on.Wikipedia.com
6. Wikipedia. Gravitaatioenergia. Haettu: vuonna.Wikipedia.com