Gibbs -vapaat energiayksiköt, miten se lasketaan, ratkaistu harjoitus

Se Gibbs vapaa energia (Yleisesti kutsutaan g) on ​​termodynaaminen potentiaali, joka on määritelty entalpia H: n erona, lukuun ottamatta lämpötilan T tuotetta, järjestelmän entropia:

G = h - t s

Gibbs -vapaa energia mitataan Joulesissa (kansainvälisen järjestelmän mukaan) Ergiosissa (yksikköjärjestelmässä), kaloreita tai elektronien volteja (Electro -volteille).

Kuvio 1. Kaavio, joka osoittaa Gibbs -energian määritelmän ja sen suhteen muihin termodynaamisiin potentiaaleihin. Lähde: Ydinvoima.netto.

Prosesseissa, jotka esiintyvät vakiopaineessa ja lämpötilassa, Gibbs -vapaan energian variaatio on ΔG = ΔH - T ΔS. Tällaisissa prosesseissa (g) edustaa järjestelmässä käytettävissä olevaa energiaa, josta voi tulla työtä.

Esimerkiksi eksotermisissä kemiallisissa reaktioissa entalpia vähenee, kun entropia kasvaa. Gibbs -toiminnassa nämä kaksi tekijää torjuu, mutta vain kun Gibbs -energia vähenee, reaktio tapahtuu spontaanisti.

Joten jos G: n variaatio on negatiivinen, prosessi on spontaani. Kun Gibbs -funktio saavuttaa minimin, järjestelmä saavuttaa vakaan tasapainon. Lyhyesti sanottuna, prosessissa, jota varten paine ja lämpötila pysyvät vakiona, voimme vakuuttaa:

- Jos prosessi on spontaani, niin ΔG < 0

- Kun järjestelmä on tasapainossa: ΔG = 0

- Ei-spontaanissa prosessissa se kasvaa: ΔG> 0.

[TOC]

Kuinka se lasketaan?

Gibbs -vapaa energia (g) lasketaan alussa annetulla määritelmällä:

G = h - T⋅s

Entalpia H puolestaan ​​on termodynaaminen potentiaali, joka on määritelty seuraavasti:

H = u + p v

- Askel askeleelta

Seuraavaksi tehdään askel -askelanalyysi, tuntemaan riippumattomat muuttujat, joista Gibbs -energia on funktio:

Ensimmäisestä termodynamiikan laista sisäinen energia liittyy järjestelmän entropiaan ja sen tilavuuteen V palautuvien prosessien suhteen differentiaalisuhteen kautta:

Se voi palvella sinua: etidiumbromidi: rakenne, ominaisuudet, käytöt, toksisuus

du = dq - dw = TDS - PDV

Tästä yhtälöstä seuraa, että sisäinen energia U on muuttujien s ja v: V:

U = u (s, v)

2- H: n määritelmästä ja differentiaalin ottamisesta saadaan:

dh = du + d (p v) = du + vdp + pdv

3- (1) saadun DU: n lausekkeen korvaaminen sinun on:

DH = TDS - PDV + VDP + PDV = TDS + VDP

Täältä pääteltään, että entalpia H riippuu entropiasta S ja Paine P: stä, eli:

H = h (s, p)

4- Nyt Gibbs-vapaan energiaeron kokonaismäärä lasketaan:

Dg = dh -tds -sdt = TDS + VDP -TDS ​​-SDT

Missä DH on korvattu kohdassa (3) löydetyllä lausekkeella.

5- Lopuksi yksinkertaistamalla saat: Dg = VDP - SDT, On selvää, että vapaa energia G riippuu paineesta ja lämpötilasta T kuten:

G = g (p, t)

- Maxwellin termodynaamiset suhteet

Edellisen osan analyysistä seuraa, että järjestelmän sisäinen energia on entropian ja tilavuuden funktio:

U = u (s, v)

Sitten ero TAI olla:

du = ∂_SU |_V Ds + ∂_VU |_S DV = TDS - PDV

Tästä ekspressiosta osittaisjohdannaisissa voidaan päätellä So -called Maxwell -termodynaamiset suhteet. Osittaisia ​​johdannaisia ​​sovelletaan, kun funktio riippuu useammasta kuin yhdestä muuttujasta ja lasketaan helposti soveltamalla seuraavan osan lause.

Maxwellin ensimmäinen suhde

 ∂_VT |_S = -Mon_SP |_V 

Päästäksesi tähän suhteeseen, Clairaut -lause - Schwarz osittaisjohdannaisilla, joissa on seuraava:

"Toisen asteen sekoitettua johdannaisia ​​vaihdettujen muuttujien kanssa ovat samat, mikäli johdettavat toiminnot ovat jatkuvia ja erilaistuvia".

Maxwellin toinen suhde

Alkaen siitä, mitä esitettiin edellisen osan 3 kohdasta:

Voi palvella sinua: liukoisuuteen vaikuttavat tekijät

H = H (S, P) ja DH = TDS + VDP

Voidaan saada:

 ∂_PT |_S = ∂_SV |_P 

Jatka samalla tavalla Gibbs -vapaan energian avulla G = g (p, t) ja Helmholtzin vapaalla energialla F = f (t, v) Maxwellin kaksi muuta termodynaamista suhdetta. 

Kuva 2. Josiah Gibbs (1839-1903) oli amerikkalainen fyysikko, kemisti ja matemaatikko, joka antoi suuren panoksen termodynamiikkaan. Lähde: Wikimedia Commons.

Maxwellin neljä termodynaamista suhdetta 

1- liittyy sisäiseen energiaan U: ∂_VT |_S = -Mon_SP |_V

2- Entalpia H: sta saatu h: ∂_PT |_S = ∂_SV |_P 

3- liittyy Helmholtz F: n energiaan: ∂_TP |_V = ∂_VS |_T 

4- Sidottu Gibbs G: n vapaaseen energiaan: ∂_TV |_P = -Mon_PS |_T

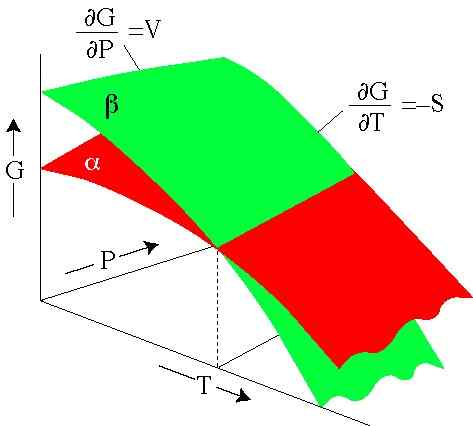Kuva 2. Gibbsin energia riippuu painosta ja lämpötilasta. Jokainen pinta edustaa vaihetta. (SERC.Carleton.Edu)

Ratkaisut

Harjoitus 1

Laske Gibbs -vapaan energian variaatio kahdelle moolille ihanteellista kaasua 300 000 lämpötilassa isotermisen laajentumisen aikana, joka johtaa 20 litran alkuperäiseen tilavuusjärjestelmään 40 litran lopulliseen tilavuuteen.

Ratkaisu

Gibbs -vapaan energian määritelmän muistaminen on:

G = h - t s

Sitten F: n rajallinen variaatio on:

Δg = ΔH - t ΔS, Koska Δt = 0

Ihanteellisissa kaasuissa entalpia riippuu vain sen absoluuttisesta lämpötilasta, mutta koska se on isoterminen prosessi, sitten ΔH = 0 ja ΔG = - T ΔS.

Ihanteellisille kaasuille isotermisen prosessin entropian vaihtelu on: 

ΔS = nr ln (v₂/V₁-A

Se sovellettiin tämän harjoituksen tapaukseen:

ΔS = 2 moolia x 8,314 j/(k mol) x ln (40L/20L) = 11,53 J/K

Sitten voimme saada muutoksen Helmholtzin energiassa:

ΔG = - 300 k x 11,53 j/k = -3457,70 J.

Harjoitus 2

Kun otetaan huomioon, että Gibbs -vapaa energia on lämpötilan ja paineen g = g (t, p) funktio; Määritä G: n vaihtelu prosessin aikana, jossa lämpötila ei muutu (isoterminen) ihanteellisen monooatoisen kaasun N -moolien kohdalla.

Voi palvella sinua: strontiumhydroksidi (sr (OH) ₂)

Ratkaisu

Kuten edellä on osoitettu, Gibbsin energian muutos riippuu vain lämpötilan T ja tilavuuden V muutoksesta, joten sen äärettömä vaihtelu lasketaan:

Dg = -sdt + vdp

Mutta jos se on prosessi, jossa lämpötila on vakio, niin DF = + VDP, joten paineen äärellinen variaatio ΔP johtaa Gibbs -energian muutokseen:

Δg = + ∫ vdp = + ∫ (n r t) dp/p = + n r t ln (Δp)

Ihanteellisen kaasuyhtälön käyttäminen:

P v = n r t

Isotermisen prosessin aikana tapahtuu, että:

D (p v) = p dv + v dp = 0

Tuo on:

DP/P = - DV/V

Joten edellinen tulos voidaan kirjoittaa tilavuuden vaihtelusta riippuen ΔV-

Δg = + ∫ vdp = + ∫ (n r t) dp/p = - ∫ (n r t) dv/v = -n r t ln (Δv)

Harjoitus 3

Seuraavan kemiallisen reaktion huomioon ottaminen:

N₂0 (g) + (3/2) tai₂ (g) ↔️No₂ g) lämpötilassa t = 298 K

Löydä Gibbs -vapaan energian variaatio ja osoita saadun tuloksen kautta, onko se spontaani prosessi.

Ratkaisu

Vaiheiden alapuolella:

- Ensimmäinen askel: Reaktion entalpit

Δhr = 2*ΔH (ei₂ (g)) - ΔH (n₂0 (g)) = 2*33,2-81,6 = -15,2 kj/mol

- Toinen vaihe: Reaktion entropian variaatio

ΔSr = 2*s (ei₂ (g)) - s (n₂0 (g)) - (3/2) s (tai₂ (g)) = 2*240,1 - 220,1 - 1,5*205,2 = -47,7 J/(mol*k).

- Kolmas vaihe: Gibbs -toiminnon variaatio

Tämä arvo määrittää tasapainon vähenevän energian ja lisääntyvän entropian välillä tietääkseen, onko reaktio lopulta spontaani vai ei.

Δgr = Δhr -t ΔSr = -15,2 -298*(-47,7) = -985,4 j/mol

Koska se on Gibbs -energian negatiivinen variaatio, se voidaan päätellä, että se on spontaani reaktio lämpötilassa 298 K = 25 ºC.

Viitteet

1. Castaños e. Ilmaiset energiaharjoitukset. Toipunut: lidiaconlachimica.WordPress.com.
2. Cengel, ja. 2012. Termodynamiikka. 7. painos. McGraw Hill.
3. Librettexts. Gibbs vapaa energia. Palautettu: Chem.Librettexts.org
4. Librettexts. Mitkä ovat ilmaista energiaa. Palautettu: Chem.Librettexts.org
5. Wikipedia. Gibbs vapaa energia. Palautettu: on.Wikipedia.com
6. Wikipedia. Gibbs vapaa energia. Haettu: vuonna.Wikipedia.com