Kitejärjestelmien käsite ja karakterisointi, tyypit, esimerkit

2713
187
Shawn Stanton II

Se kiteiset järjestelmät Ne ovat joukko geometrisiä ominaisuuksia ja symmetriaelementtejä, jotka sallivat luokittelun erilaisten kidekkonglomeraattien luokittelusta. Siten sen sivujen suhteellisista pituuksista riippuen kulma sen kasvojen, sisäisten akselien ja muiden geometristen näkökohtien välinen kulma, kidepäiden muoto, joka eroaa itsestään toisesta.

Vaikka kiteiset järjestelmät liittyvät suoraan mineraalien, metallien, epäorgaanisten tai orgaanisten yhdisteiden kiteiseen rakenteeseen, ne viittaavat enemmän ulkoisen muodon ominaisuuksiin, eivätkä niiden atomien, ionien tai molekyylien sisäisen hävittämisen yhteydessä.

Mineralogisten kiteiden ja niiden symmetrioiden rikas monimuotoisuus tukevat kuusi kiteistä järjestelmää. Lähde: Pexels.

Kuusi kiteistä järjestelmää ovat kuutiometriä, tetragonaalisia, kuusikulmaisia, orthromisia, monokliinisiä ja kolmipyöriä. Kuusikulmaisesta järjestelmästä johdetaan trigonaalisesta tai rhomboedista. Mikä tahansa sen puhtaan tilassa karakterisoinnin jälkeen se kuuluu johonkin näistä kuudesta järjestelmästä.

Luonnossa joskus riittää katsomaan kiteitä tietääksesi mihin järjestelmään he kuuluvat; Edellyttäen, että kristallografian hallitseminen on selkeä. Usein tämä on kuitenkin vaivalloista työtä, koska kiteet ovat "sekoitettuja" tai "muodonmuutos", ympäristöolosuhteiden tuote kasvun aikana.

[TOC]

Käsite ja karakterisointi

Kiteiset järjestelmät periaatteessa voi tuntua abstraktilta ja vaikealta ymmärtää. Luonnossa se ei etsi kiteitä, joilla on kuution tarkka muoto; Mutta jaa tämän kaikkien geometristen ja isometrian ominaisuuksien kanssa. Jopa tätä silmällä pitäen, voi edelleen olla mahdotonta selvittää, mikä kiteinen järjestelmä kuuluu kopioon.

Tätä varten on olemassa instrumentaalisia karakterisointitekniikoita, jotka niiden tulosten joukossa osoittavat arvot tietyille parametreille, jotka paljastavat, mikä kiteinen järjestelmä on tutkittava; Ja lisäksi se viittaa lasin kemiallisiin ominaisuuksiin.

Kiteiden suosikkitekniikka on siksi x -rayn kristallografia; Erityisesti x -rayn diffraktiojauhe.

Se voi palvella sinua: ammoniumkloridi (NH4CL)

Yhteenvetosanat: X -säde on vuorovaikutuksessa lasin kanssa ja saadaan diffraktiokuvio: sarja samankeskisiä pisteitä, joiden muoto riippuu hiukkasten sisäisestä järjestyksestä. Tietojen käsittely, se lopulta laskee yksikkösolun parametrit; Ja tällä kiteinen järjestelmä määritetään.

Jokainen kiteinen järjestelmä koostuu kuitenkin kiteisistä luokista, jotka yhteensä 32. Näistä erilaisista lisämuodoista johdetaan myös. Siksi kiteet ovat hyvin monipuolisia.

Kiteisten järjestelmien tyypit

Kuutio tai isometrinen

Kuutio on vain yksi kiteisistä luokista, joka sisältää kuutiojärjestelmän. Lähde: Smiddle [CC BY-SA (http: // creativecommons.Org/lisenssit/by-SA/3.0/]]

Kuutio- tai isometrinen järjestelmä vastaa erittäin symmetrisiä kiteitä. Esimerkiksi kuutio esittelee sarjan symmetriaoperaatioita, jotka kuvaavat sitä. Kuvittelemme kuution keskellä ristiä, joka koskettaa yläpuolella olevia kasvoja, pohjaa ja sivuja. Etäisyydet ovat samat ja siepataan suorassa kulmassa.

Jos kristalli täyttää kuution symmetrian, vaikka sillä ei olisikaan juuri sitä muotoa, se kuuluu tähän kiteiseen järjestelmään.

Juuri täällä viisi kiteistä luokkaa, jotka muodostavat kuutiojärjestelmän: kuutio, oktaedri, rhombinen dodekaedri, icositerahedro ja heksacisoedro on esitetty. Jokaisella luokalla on omat variantinsa, jotka voivat myös katkaistua (tasaisilla kärkipisteillä).

Tetragonaali

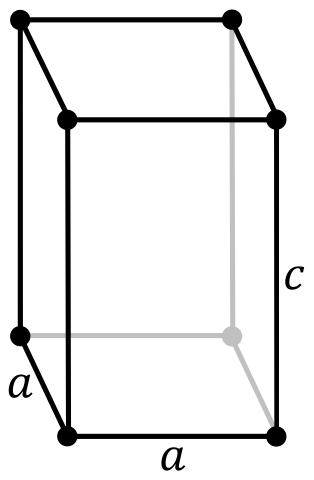Tetragonaaliyksikkö. Lähde: Stannered Wikipedian kautta.

Tetragonaalinen järjestelmä voidaan visualisoida ikään kuin se olisi suorakulmio, jolle tilavuus on annettu. Toisin kuin kuutio, sen akseli c on pidempi tai lyhyempi kuin sen akselit -lla. Sitä voidaan nähdä myös kuutiona, joka on venytetty tai pakattu.

Voi palvella sinua: Stoikiometriset laskelmat

Kiteiset luokat, jotka muodostavat tetragonaalisen järjestelmän, ovat serkkuja ja neljää puolta pyramidia, kahdeksan sivun kaksoispyramidit, trapetsoderit ja taas icositerahedro ja heksacisoedro. Ellei sinulla ole paperilukuja käsillä, on vaikea tunnistaa näitä muotoja ilman vuosien kokemuksen apua.

Kuusikulmainen

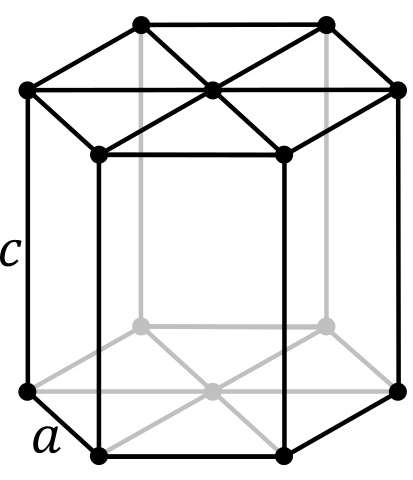Kuusikulmainen yksikkö. Lähde: Stannered Wikipedian kautta.

Mikä tahansa kiteinen muoto, jonka emäs vastaa kuusikulmion, kuuluu kuusikulmaiseen kiteiseen järjestelmään. Jotkut sen kiteisistä luokista ovat: kahdentoista sivun ja kaksinkertaisen pyramidin pyramidit.

Trigonaalinen

Kristalli, joka kuuluu trigonaaliseen järjestelmään, on myös kuusikulmainen; Mutta sen sijaan, että heillä olisi kuusi puolta, heillä on kolme. Hänen kiteiset luokansa ovat: kolmen puolet prismat tai pyramidi.

Ortorominen

Ortorromisessa järjestelmässä niiden kiteillä on rhomboédica -pohja, joka on peräisin muodoista, joiden kolmella akselilla on eri pituudet. Hänen kiteiset luokansa ovat: bipiramidaaliset, biesfenoidiset ja gag.

Monokliininen

Tällä kertaa monokliinisessä järjestelmässä pohja on yhdensuuntainen ohjelma eikä rhombus. Hänen kiteiset luokansa ovat: Sphenoidiset ja kolmen puolet prismat.

Trikliininen

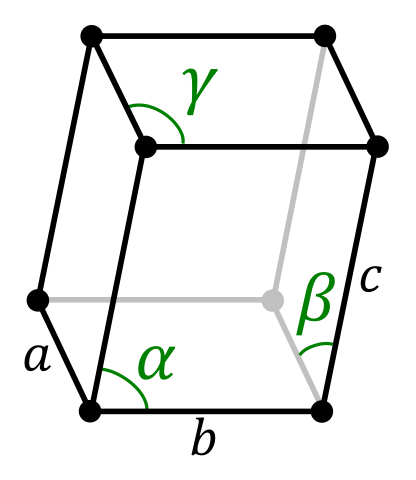Trikliininen yksikkö. Lähde: Stannered Wikipedian kautta.

Trisykliiniseen järjestelmään kuuluvat kiteet ovat epäsymmetrisiä. Aluksi kaikilla sen akseleilla on eri pituudet, samoin kuin heidän kasvonsa kulmat, jotka ovat kaltevia.

Täältä tulee hänen nimensä: kolme kaltevaa, trichllinic -kulmaa. Nämä kiteet sekoitetaan usein ortorromisiin, kuusikulmaisiin ja omaksuvat myös pseudokubisia muotoja.

Sen kiteisten luokkien joukossa ovat pinakoidit, jalkakäytävät ja muodot, joissa on lukumäärä kasvoja.