Helmholtz -vapaat energiayksiköt, miten se lasketaan, ratkaistu harjoitukset

Se Helmholtz ilmainen energia Se on termodynaaminen potentiaali, joka mittaa suljetun järjestelmän hyödyllistä työtä vakiona lämpötila- ja tilavuusolosuhteissa. Helmholtzin ilmainen energia merkitään nimellä F Ja se määritellään eroksi sisäisestä energiasta TAI Vähemmän lämpötilatuote T Entropialle S-

F = u - t⋅s

Koska se on energiaa, se mitataan kansainvälisen järjestelmän Joulesissa (SI), vaikka muut asianmukaiset yksiköt voivat olla myös ERGIOS (CGS), kaloreita tai elektronien voltteja (EV).

Kuvio 1. Määritelmä Helmholtzin energia. Lähde: Pixabay.

Helmholtzin energian negatiivinen variaatio prosessin aikana rinnastetaan suurimmalla työllä, jonka järjestelmä voi suorittaa isocoric -prosessissa, toisin sanoen vakiotilavuuden suhteen. Kun tilavuus ei ole vakio, osa tästä työstä voidaan tehdä ympäristössä.

Tässä tapauksessa viitataan työhön, jossa tilavuus ei vaihtele, kuten sähköinen työ: dw = φdq, φ sähköpotentiaalina ja q sähkövarauksena.

Jos lämpötila on myös vakio, Helmholtzin energia minimoidaan, kun tasapaino saavutetaan. Kaiken tämän suhteen Helmholtzin energia on erityisen hyödyllinen vakiotilavuusprosesseissa. Tässä tapauksessa sinulla on:

- Spontaanille prosessille: ΔF < 0

- Kun järjestelmä on tasapainossa: ΔF = 0

- Ei-spontaanissa prosessissa: Δf> 0.

[TOC]

Kuinka Helmholtz vapaa energia lasketaan?

Kuten alussa todettiin, Helmholtzin energia määritellään "sisäiseksi energiaksi tai järjestelmäksi, lukuun ottamatta järjestelmän absoluuttisen T -lämpötilan tuotetta järjestelmän entropialla":

F = u - t⋅s

Se on lämpötilan T ja tilavuuden V funktio. Vaiheet tämän visualisointiin ovat seuraavat:

Voi palvella sinua: sisäiset elektronit

- Alkaen termodynamiikan ensimmäisestä laista, sisäisestä energiasta tai liittyy järjestelmän entropiaan ja sen tilavuuteen V palautuvien prosessien suhteen seuraavan differentiaalisen suhteen kautta:

du = dq - dw = TDS - PDV

Tämä seuraa, että sisäinen energia tai on muuttujien funktio S ja V, siksi:

U = u (s, v)

- Nyt määritelmä F Ja se on johdettu:

df = du - d (ts) = du - tds - sdt

- Korvaamalla siellä ensimmäisessä vaiheessa DU: lle saatu differentiaalinen lauseke pysyy:

Df = TDS - PDV - TDS - SDT = -SDT - PDV

- Lopuksi päätellään, että F on lämpötilan T ja tilavuuden V funktio ja se voidaan ilmaista seuraavasti:

F = f (t, v)

Kuva 2. Saksan fyysikko ja lääkäri Hermann von Helmholtz (1821-1894), joka tunnusti hänen panoksestaan ​​sähkömagneettisuuteen ja termodynamiikkaan, muun muassa tieteen alueiden joukossa. Lähde: Wikimedia Commons.

Spontaanit prosessit

Helmholtzin energiaa voidaan soveltaa yleisenä spontaanisuuden kriteerinä eristetyissä järjestelmissä, mutta ennen joitain käsitteitä olisi määritettävä:

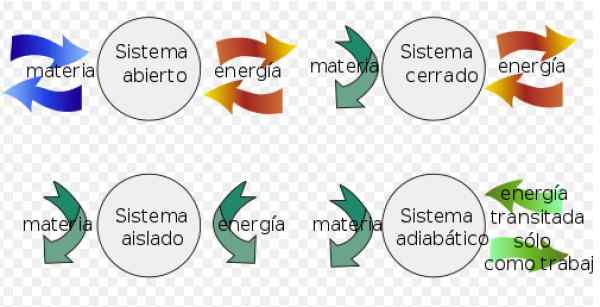
- Eräs järjestelmä suljettu Se voi vaihtaa energiaa ympäristön kanssa, mutta ei voi vaihtaa asiaa.

- Sen sijaan a eristetty järjestelmä ei vaihda asiaa tai energiaa ympäristön kanssa.

- Lopuksi a avoin systeemi Vaihda asiaa ja energiaa ympäristön kanssa. 

Kuva 3. Termodynaamiset järjestelmät. Lähde: Wikimedia Commons. Fjgar (bis) [cc by-sa (https: // creativecommons.Org/lisenssit/by-SA/4.0)].

Palautuvissa prosesseissa sisäisen energian vaihtelu lasketaan seuraavasti:

Du = TDS - PDV

Oletetaan nyt, että vakiotilavuus (isokorjainen) prosessi, jossa edellisen lausekkeen toisella termillä on nolla -panos. On myös muistettava, että Clausius -epätasa -arvo: 

DS ≥ DQ/T

Tällainen eriarvoisuus koskee eristettyä termodynaamista järjestelmää.

Niin, että prosessissa (palautettavissa tai ei), jossa tilavuus ylläpidetään vakiona, toteutetaan:

Voi palvella sinua: fosforihappo (H3PO4)

T ds ≥ du (Kiinteällä tilavuudella)

Ottaen huomioon:

df = du - t ds 

Meidän on täytettävä isokorjaisessa prosessissa vakiona lämpötilassa, että: Df ≤ 0, Kuten alussa on osoitettu.

Joten Helmholtz F: n energia on vähenevä määrä spontaanissa prosessissa, kun se on eristetty järjestelmä. F saavuttaa vähimmäis- ja vakaan arvonsa, kun palautuva saldo on saavutettu.

Ratkaisut

Harjoitus 1

Laske Helmholtz F: n vapaan energian vaihtelu 2 moolia ihanteellisen kaasun kohdalla 300 000 lämpötilassa isotermisen laajennuksen aikana, joka johtaa 20 litran alkuperäisen tilavuuden järjestelmään 40 litran lopulliseen tilavuuteen.

Ratkaisu

Alkaen f: n määritelmästä:

F = u - t s

Sitten F: n äärellinen variaatio, nimeltään ΔF, on:

Δf = Δu - t ΔS

Kuten lausunnossa todetaan, että lämpötila on vakio: Δt = 0. Ihanteellisissa kaasuissa sisäinen energia riippuu kuitenkin vain sen absoluuttisesta lämpötilasta, mutta koska se on isoterminen prosessi, sitten ΔU = 0 ja Δf = - t ΔS. Ihanteellisille kaasuille isotermisen prosessin entropian vaihtelu on kirjoitettu näin: 

ΔS = n.R -.ln (v₂/V₁-A

Tämän ilmaisun soveltaminen:

ΔS = 2 moolia x 8,314 j/(k mol) x ln (40L/20L) = 11,53 J/K

Lopuksi, muutos Helmholtzin energiassa on:

Δf = - t ΔS = - 300k x 11,53 J/k = -3457,70 J.

Harjoitus 2

Sylinterin sisällä on mäntä, joka jakaa sen kahteen osaan ja männän molemmille puolille n Ihanteellisen monoatoisen kaasun moolit, kuten alla olevassa kuvassa esitetään.

Sylinterin seinät ovat hyviä lämpöjohtimia (diaterisia) ja ovat kosketuksissa T -lämpötilasäiliön kanssa_jompikumpi.

Kunkin sylinteriosan alkutilavuus on V_1i ja v_2i, Vaikka sen lopulliset volyymit ovat V_1F ja v_2F Kvasiestisen siirtymisen jälkeen. Mäntä liikkuu männän avulla, joka ylittää hermeettisesti kaksi sylinterin tapasia.

Se voi palvella sinua: Tecnecio (TC): rakenne, ominaisuudet, käytöt, hankkiminen

Sitä pyydetään löytämään:

a) kaasun sisäisen energian muutos ja järjestelmän ja järjestelmän tekemä työ

b) Helmholtzin energian vaihtelu.

Liittää jhk

Kun mäntä liikkuu lähes, männään kohdistuvan ulkoisen voiman on tasapainotettava voima sylinterin kahden osan paineeron vuoksi.

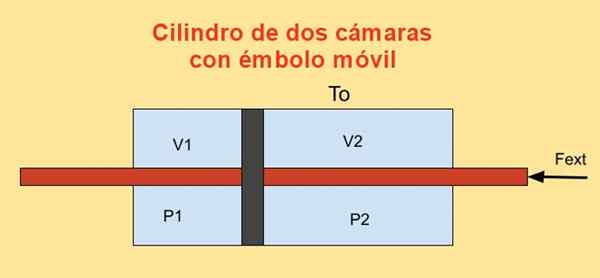Kuva 4. Vapaan energian F variaatio sylinterissä, jossa on kaksi kameraa. Lähde: f. Zapata.

Työ Dw Valmistettu ulkoinen voima F_alanumero äärettömän siirtymän aikana Dx On:

Dw = - f_alanumero Dx = (p₁ - P₂) A dx = p₁ DV₁ + P₂ DV₂

Missä suhdetta on käytetty DV₁ = - DV₂ = DX, olemus -lla Männän alue. Toisaalta Helmholtzin energian variaatio on: 

Df = -sdt - pdv

Koska prosessin aikana lämpötila ei muutu, silloin dt = 0 ja Df = - pdv. Tämän lausekkeen soveltaminen sylinterisi jokaiseen osaan:

dw = p₁ DV₁ + P₂ DV₂ = - DF₁ - Df₂

Olemus F₁  ja F₂ Helmholtzin energiat jokaisessa kamerassa.

Raja W -työ voidaan laskea Helmholtzin jokaisen kameran energian äärellisestä variaatiosta:

W = -Af₁ - Δf₂

Ratkaisu b

Jos haluat löytää energian muutoksen Helmholtzista, määritelmää käytetään: F = u - t s. Kuten jokaisessa kamerassa sinulla on ihanteellinen monoatominen kaasu vakiona lämpötilassa T_jompikumpi, Sisäinen energia ei muutu (ΔU = 0), niin että: Δf = - t_jompikumpi ΔS. Sitä paitsi:

ΔS = nr ln (v_F/Näin)

Se korvaamalla se mahdollistaa lopulta tehdyn työn: 

W = -t_jompikumpi Nr Ln (V_1F /V_1i) -Nr Ln (V_2F /V_2i) = -Af₁ -Δf₂

W = - NR LN: lle [(V_1F ⋅ V_1i)/(V_{2F .}V_2i)] = - ΔF_{kaikki yhteensä}

Olemus Δf_{kaikki yhteensä} Helmholtzin energian kokonaisvaihtelu.

Viitteet

1. Castaños e. Ilmaiset energiaharjoitukset. Toipunut: lidiaconlachimica.WordPress.com
2. Librettexts. Helmholtz Energy. Palautettu: Chem.Librettexts.org
3. Librettexts. Mitkä ovat ilmaista energiaa. Palautettu: Chem.Librettexts.org
4. Wikipedia. Helmholtz Energy. Palautettu: on.Wikipedia.com
5. Wikipedia. Helmholtz ilmainen energia. Haettu: vuonna.Wikipedia.com