Mekaaniset energiakaavat, konsepti, tyypit, esimerkit, harjoitukset

Se mekaaninen energia esine tai järjestelmä määritellään sen potentiaalisen energian ja kineettisen energian summana. Kuten nimestä voi viitata, järjestelmä hankkii mekaanista energiaa mekaanisten voimien, kuten painon ja elastisen voiman, ansiosta.

Kehon mekaanisen energian määrän mukaan sillä on myös kyky suorittaa mekaaninen työ.

Kuvio 1. Roller -vuoristoautoliike voidaan kuvata säästämällä mekaanista energiaa. Lähde: Pixabay.

Energia - tyyppi, joka on - on skalaarinen määrä, siten puuttuu suunta ja merkitys. Olla JA_m Esineen mekaaninen energia, TAI sen potentiaalinen energia ja K -k - Sen kineettinen energia, kaava sen laskemiseksi on:

JA_m = K + u

Kaikenlaisen kansainvälisen energiajärjestelmän yksikkö on Joule, joka lyhennetään J: ksi. 1 J vastaa 1 n.m (Newton metriä kohti-A.

Kineettisen energian suhteen se lasketaan seuraavasti:

K = ½ m.v²

Missä m Se on esineen massa ja v Sen nopeus. Kineettinen energia on aina positiivinen määrä, koska nopeuden massa ja neliö ovat. Mitä potentiaaliseen energiaan, jos kyse on gravitaatiopotentiaalienergiasta, sinulla on:

U = m.g.h

Tässä m Se on edelleen taikina, g Se on painovoiman kiihtyvyys ja h Se on korkeus suhteessa vertailutasoon tai jos se on edullinen, maa.

Nyt, jos kyseisellä keholla on joustava potentiaalienergia, se voi olla jousi -se johtuu siitä, että se on pakattu tai ehkä pitkänomainen. Tällöin siihen liittyvä potentiaalinen energia on:

U = ½ kx²

Kanssa k -k - kuten jousvakio, mikä osoittaa kuinka helppoa tai vaikeaa on muodonmuutos ja x Mainitun muodonmuutoksen pituus.

[TOC]

Mekaanisen energian käsite ja ominaisuudet

Aikaisemmin annettua määritelmää, mekaaninen energia riippuu sitten kehon liikkeeseen liittyvästä energiasta: kineettistä energiaa sekä potentiaalienergian vaikutusta, joka, kuten totesimme kunnioitus maaperään tai vertailutasoon.

Tarjotaan tätä yksinkertaisella esimerkillä: Oletetaan, että sinulla on potti lattialla ja levossa. Koska se on vielä, sillä ei ole kineettistä energiaa, ja se on myös maassa, paikka, josta se ei voi pudota; Siksi siitä puuttuu gravitaatiopotentiaalienergia ja sen mekaaninen energia on 0.

Oletetaan nyt, että joku asettaa potin vain katon tai ikkunan reunaan, 3.0 metriä korkea. Tätä varten henkilön oli tehtävä työ painovoimaa vastaan. Potissa on nyt gravitaatiopotentiaalienergia, se voi pudota siitä korkeudesta ja sen mekaaninen energia ei ole enää tyhjyyttä.

Kuva 2. Ikkunan päällä olevassa potissa on painovoimapotentiaalienergia. Lähde: Pixabay.

Näissä olosuhteissa potissa on JA_m = U Ja tämä määrä riippuu potin korkeudesta ja painosta, kuten aiemmin osoitetaan.

Oletetaan, että ruukku putoaa, koska se oli epävarmassa asemassa. Sen nopeuden kasvaessa ja sen kanssa sen kineettinen energia, kun taas gravitaatiopotentiaalienergia vähenee, koska se menettää korkeuden. Mekaaninen energia milloin tahansa putoamishetkellä on:

Voi palvella sinua: mitkä ovat johdetut suuruudet?

JA_m = U + k = ½ m.v² + m.g.h  

Konservatiiviset ja ei-konservatiiviset voimat

Kun ruukku on tietyllä korkeudella, sillä on gravitaatiopotentiaalienergia, koska kuka sitä kiipesi, teki työn painovoimaa vastaan. Tämän työn suuruus on saman arvoinen kuin se, joka tekee painovoimaa, kun potti putoaa Samasta korkeudesta, mutta sillä on vastakkainen merkki, koska se tehtiin sitä vastaan.

Työt, jotka voimat, kuten painovoima ja joustavuus. Ei ole väliä seurannut etenemissuuntainen siirtyminen yhdestä toiseen, vain arvoilla on merkitystä. Voimia, jotka käyttäytyvät tällä tavalla Konservatiiviset voimat.

Ja koska ne ovat konservatiivisia, ne sallivat heidän tekemänsä työn tallentamisen potentiaaliseksi energiaksi objektin tai järjestelmän kokoonpanossa. Siksi ikkunan tai katon reunalla olevalla astialla oli mahdollisuus pudota ja sen mukana liikkeen kehittämiseksi.

Toisaalta on voimia, joiden teokset riippuvat polusta, jota seuraa esine, johon ne toimivat. Kitka kuuluu tämän tyyppisiin voimiin. Kengän pohjat vietetään enemmän, kun siirryt paikasta toiselle tiellä, jossa on monia kierroksia, kuin kun menet toiseen.

Kitkavoimat tekevät työn, joka vähentää kehon kineettistä energiaa, koska se hidastaa niitä. Ja siksi niiden järjestelmien mekaaninen energia.

Osa voimalla tehdystä työstä menetetään esimerkiksi lämmöllä tai äänellä.

Mekaanisen energian tyypit

Mekaaninen energia on, kuten totesimme, kineettisen energian ja potentiaalienergian summa. Nyt potentiaalista energiaa voi tulla erilaisista konservatiivisista voimista: paino, joustava lujuus ja sähköstaattinen voima.

- Kineettinen energia

Kineettinen energia on skalaarinen määrä, josta tulee aina liike. Kaikissa hiukkasissa tai liikkuvassa esineissä on kineettinen energia. Suorassa linjassa liikkuvalla esineellä on käännösten kineettinen energia. Sama tapahtuu, jos se pyörii, tässä tapauksessa puhuu kiertokineettisen energian puhetta.

Esimerkiksi tien varrella liikkuvalla autolla on kineettinen energia. Myös jalkapallopallo liikkuessaan kentällä tai kiireellisesti kävelevä henkilö päästäkseen toimistoon.

- Mahdollinen energia

On aina mahdollista yhdistää skalaarifunktio, jota kutsutaan potentiaaliseksi energiaksi konservatiiviseen voimaan. Seuraavat ovat erottuvia:

Gravitaatiopotentiaalienergia

Sellainen. Esimerkiksi joku, joka on levossa 10 -luvun rakennuksen terassilla, on potentiaalista energiaa 0 terassin maan suhteen, mutta ei kadun suhteen, joka on 10 lattia.

Elastinen potentiaalienergia

Sitä varastoidaan yleensä esineisiin, kuten liigaihin ja jousiin, jotka liittyvät muodonmuutoksiin, joita he kokevat niitä venyttäessään tai puristettaessa.

Sähköstaattinen potentiaalienergia

Sitä tallennetaan tasapainon sähkökuormitusjärjestelmään, koska niiden välillä on sähköstaattinen vuorovaikutus. Oletetaan, että samasta erillisestä merkistä on kaksi sähkövarausta pienellä etäisyydellä; Koska saman merkin sähkömaksut hylätään, ulkoisen edustajan odotetaan tekevän työtä saadakseen ne lähemmäksi.

Voi palvella sinua: vaihtovirtapiirit: tyypit, sovellukset, esimerkit

Kun se on sijoitettu, järjestelmä onnistuu tallentamaan agentin tekemän työn määrittämiseksi sähköstaattisen potentiaalin energian muodossa.

Mekaanisen energian säilyminen

Palaa putoavaan pottiin, sen gravitaatiopotentiaalienergiaa, kun se oli katon reunalla, muuttuu liikkeen kineettiseksi liikkeeksi. Tämä kasvaa ensimmäisen kustannuksella, mutta molempien summa pysyy vakiona, koska potin kaatuminen aktivoituu painovoimalla, mikä on konservatiivinen voima.

Yhden energian tyypin ja toisen välillä on vaihto, mutta alkuperäinen määrä on sama. Siksi on pätevä vahvistaa, että:

Alkuperäinen mekaaninen energia = lopullinen mekaaninen energia

JA_{Alkuperäinen m} = E_{M lopullinen}

Vaihtoehtoisesti:

K -k -_alkukirjain + TAI_alkukirjain = K _lopullinen + TAI_lopullinen

Toisin sanoen mekaaninen energia ei muutu ja ∆E_m = 0. "∆" -symboli tarkoittaa vaihtelua tai eroa lopullisen määrän ja alkuperäisen välillä.

Mekaanisen energian säilyttämisen periaatteen soveltamiseksi ongelmanratkaisuun on tarpeen:

-Se pätee vain silloin, kun järjestelmään vaikuttavat voimat ovat konservatiivisia (vakavuus, joustava ja sähköstaattinen). Siinä tapauksessa: ∆E_m = 0.

-Tutkimusjärjestelmä on eristettävä. Energiansiirtoa ei ole millään tavalla.

-Jos ongelmateoksessa ilmestyy ongelma, niin ∆E_m ≠ 0. Silti ongelma voitaisiin ratkaista etsimällä konservatiivisten voimien tekemä työ, koska se on syynä mekaanisen energian vähentymiseen.

Mekaanisen energian säilyttämisen vähennys

Oletetaan, että konservatiivinen voima vaikuttaa järjestelmään, joka tekee työtä W -. Tämä työ aiheuttaa kineettisen energian muutoksen:

W = ∆k (Kasellinen työ-energialause)

On tärkeää huomata, että työenergialausekinettinen kineettinen voidaan soveltaa jopa ei-konservatiivisten voimien tapauksessa.

Toisaalta työ on vastuussa myös potentiaalisen energian muutoksesta, ja konservatiivisen voiman tapauksessa potentiaalienergian muutos määritellään kyseisen työn negatiiviseksi:

W = -∆u

Näiden yhtälöiden sovittaminen, koska molemmat viittaavat objektin työhön:

∆K = -∆U 

K -k -_F - K -k -_jompikumpi = -(u_F - TAI_jompikumpi-A

Tilaukset symboloivat "lopullista" ja "alkuperäistä". Ryhmittely:

K -k -_F + TAI_F = K_jompikumpi + TAI_jompikumpi                                                    

Esimerkkejä mekaanisesta energiasta

Monissa esineissä on monimutkaisia ​​liikkeitä, joissa on monimutkaista löytää lausekkeita sijainnille, nopeudelle ja kiihtyvyydelle ajan funktiona. Tällaisissa tapauksissa mekaanisen energian säilyttämisperiaatteen soveltaminen on tehokkaampi menettely kuin yrittää soveltaa suoraan Newtonin lakeja.

Katsotaanpa joitain esimerkkejä, joissa mekaaninen energia säilyy:

-Hiihtäjä, joka liukuu alamäkeen lumisten kukkuloiden yli, edellyttäen, että kitkan puuttuminen oletetaan. Tässä tapauksessa paino on liikkeen aiheuttava voima koko radan ajan.

-Venäjän vuoristokärryt, Se on yksi tyypillisimmistä esimerkeistä. Tässä myös paino on voima, joka määrittelee liikkeen ja mekaanisen energian säilyttämisen, jos kitkaa ei ole.

Voi palvella sinua: ionisaatioenergia

-Yksinkertainen heiluri Se koostuu massasta, jolla on kiistaton köysi -Se ei muuta pituutta -joka erottuu lyhyesti pystysuunnasta ja sen annetaan värähdellä. Tiedämme, että se lopulta pysähtyy kitkan vuoksi, mutta kun kitkaa ei oteta huomioon, myös mekaaninen energia säilyy.

-Lohko, joka vaikuttaa jouseen kiinnitetty toiseen päähän seinään, kaikki laitetaan erittäin sileälle pöydälle. Lohko puristaa jousen, kulkee tietyn etäisyyden ja ammutaan sitten vastakkaiseen suuntaan, koska jousi venyy. Täällä lohko saa potentiaalisen energiansa työn ansiosta, joka tekee siitä kevään.

-Kevät ja pallo: Kun pallo purkaa jousen, tämä pomppiva. Tämä johtuu siitä, että kun kevät vapautuu, potentiaalisesta energiasta tulee kineettinen energia pallossa.

-Trampoliinihyppy: Se toimii samanlaisena kuin keväällä, mainostaen hänen luokseen hyppäävää henkilöä. Tämä hyödyntää painoa hyppääessään, jonka kanssa se muodonmuutos trampoliinia, mutta tämä, kun palattiin alkuperäiseen sijaintiinsa, antaa impulssin hyppääjälle.

Kuva 3. Ponnahduslauta toimii keväänä, mainostaen sitä, jotka hyppäävät siihen. Lähde: Pixabay.

Ratkaisut

- Harjoitus 1

Massan kohde M = 1 kg pudotetaan rampilla 1 m: n korkeudesta. Jos ramppi on erittäin sileä, laske kehon nopeus juuri kun jousi törmää.

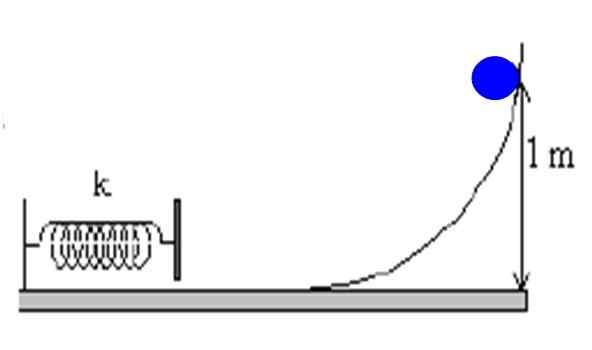Kuva 4. Kohde laskeutuu rampilla ilman kitkaa ja puristaa seinään kiinnitetyn jousen. Lähde: f. Zapata.

Ratkaisu

Lausunnossa todetaan, että ramppi on sileä, mikä tarkoittaa, että ainoa kehoon vaikuttava voima on sen paino, konservatiivinen voima. Siten on osoitettu soveltavan mekaanisen energian säilyttämistä radan kaikkien pisteiden välillä.

Harkitse kuvassa 5 merkittyjä pisteitä: a, b ja c.

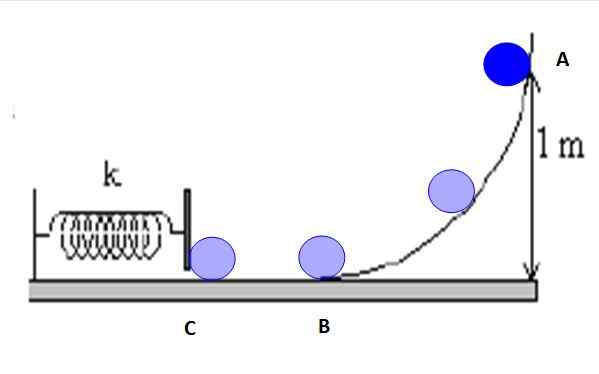Kuva 5. Kohteen seuraava polku on kitka ja mekaaninen energia säilyy minkä tahansa pisteparin välillä. Lähde: f. Zapata.

On mahdollista määrittää energian säilyttäminen A: n, B: n ja C: n tai A: n ja C: n välillä tai minkä tahansa rampin välipisteistä. Esimerkiksi A: n ja C: n välillä sinulla on:

Mekaaninen energia a = mekaaninen energia C: ssä

JA_mehu = E_MC

K -k -_-Lla + TAI_-Lla = K_C + TAI_C

½ m.v_-Lla² + m.g.h_-Lla = ½ m v_C² + m.g.h_C

Kuten pisteestä A, nopeus V_-Lla = 0, toisaalta H_C = 0. Lisäksi massa peruutetaan, koska se on yleinen tekijä. Niin:

g.h_-Lla = ½ V_C²

v_C²= 2 g.h_-Lla

- Harjoitus 2

Löydä maksimaalinen puristus, jonka harjoituksen jousi ratkaistu 1 kokee, jos saman joustava vakio on 200 n/m.

Ratkaisu

Jousen joustava vakio osoittaa, että voima levitetään muodonmuutokseen pituusyksikön muodonmuutos. Koska tämän kevään vakio on arvon arvoinen K = 200 n/m, tämä osoittaa, että sen puristamiseen tai venyttämiseen tarvitaan 200 N 1 m.

Olla x Etäisyys, jonka objekti puristaa jousen ennen kuin pysähtyy pisteeseen D:

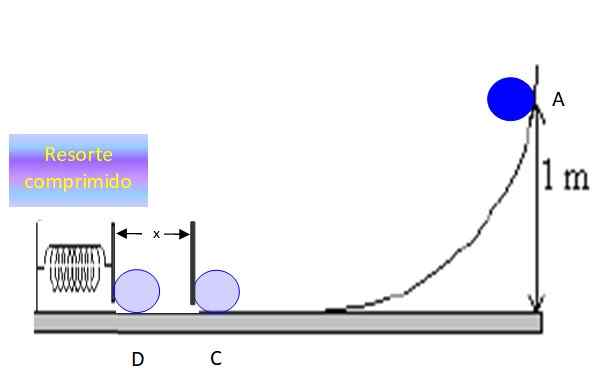Kuva 6. Objekti puristaa jousen x -etäisyyden ja pysähtyy hetkeksi. Lähde: f. Zapata.

Pisteiden C ja D välisen energian säilyttäminen osoittaa, että:

K -k -_C + TAI_C = K_{D -d} + TAI_{D -d}

Kohdassa C siinä ei ole gravitaatiopotentiaalienergiaa, koska sen korkeus on 0, mutta siinä on kineettinen energia. D: ssä hän on pysähtynyt kokonaan, siksi siellä_{D -d} = 0, mutta sen sijaan sinulla on käytettävissään pakatun jousen u potentiaalinen energia_{D -d}.

Mekaanisen energian säilyttäminen on edelleen:

K -k -_C = U_{D -d}

½ MV_C² = ½ kx²

 

Viitteet

1. Bauer, W. 2011. Fysiikka tekniikkaan ja tieteisiin. Osa 1. MC Graw Hill.
2. Figueroa, D. 2005. Sarja: Tieteen ja tekniikan fysiikka. Osa 1. Kinematiikka. Toimittanut Douglas Figueroa (USB).
3. Ritari, r.  2017. Tutkijoiden fysiikka ja tekniikka: strategialähestymistapa. Pearson.
4. Sears, Zemansky. 2016. Yliopiston fysiikka, jolla on moderni fysiikka. 14. päivä. Ed. Osa 1.
5. Wikipedia. Mekaaninen energia.Palautettu: on.Wikipedia.org.