Potentiaaliset energiaominaisuudet, tyypit, laskelmat ja esimerkit

Se Mahdollinen energia Se on energia, joka ruumiilla on kokoonpanossaan. Kun esineet ovat vuorovaikutuksessa, on voimia, jotka kykenevät tekemään työtä, ja tämä kyky tehdä työtä, joka on tallennettu heidän asennukseensa, voi kääntyä energiaksi.

Esimerkiksi ihmiset ovat hyödyntäneet veden potentiaalista energiaa muinaisista ajasta lähtien, ensimmäiset kehruutehtaat ja sitten vesivoimalaitokset.

Niagaran putoukset: valtava gravitaatiopotentiaalienergiavaraus. Lähde: Pixabay.

Toisaalta monilla materiaaleilla on huomattava kyky tehdä työtä muodonmuutoksella ja palaamalla sitten alkuperäiseen kokoonsa. Ja muissa olosuhteissa sähkövarauksen järjestely mahdollistaa sähköpotentiaalin energian, kuten lauhduttimen, säilyttämisen.

Potentiaalinen energia tarjoaa monia mahdollisuuksia muuttua muiksi hyödyllisiksi energiamuodoiksi, joten sitä hallitsevien lakien tuntemisen tärkeys. 

[TOC]

Potentiaalisen energian alkuperä

Kohteen potentiaalisella energialla on alkuperänsä siihen vaikuttavista voimista. Potentiaalinen energia on kuitenkin skalaarinen, kun taas voimat ovat vektoria. Siksi potentiaalisen energian määrittämiseksi riittää osoittamaan sen numeerisen arvon ja valitut yksiköt.

Toinen tärkeä laatu on voimatyyppi, jolla potentiaalienergiaa voidaan tallentaa, koska mikään voima ei ole tätä hyvettä. Vain konservatiiviset voimat varastoivat potentiaalista energiaa järjestelmissä, joissa ne toimivat.

Konservatiivinen voima on se, jolle työ ei riipu esineen seuraavista etenemissuunnasta, vaan vain lähtökohdasta ja saapumispisteestä. Veden putoamisen lisäävä voima on painovoima, joka on konservatiivinen voima.

Toisaalta joustavat ja sähköstaattisella voimilla on myös tämä laatu, siksi niihin liittyy potentiaalista energiaa.

Joukot, jotka eivät täytä edellä mainittua vaatimusta, niitä kutsutaan ei -konservatiivisiksi; Esimerkki heistä on kitkaa ja ilmankestävyyttä.

Potentiaalisen energian tyypit

Koska potentiaalienergia johtuu aina jo mainituista konservatiivisista voimista, kuten jo mainitut, gravitaatiopotentiaalienergiasta, elastisesta potentiaalienergiasta, sähköstaattisesta potentiaalienergiasta, ydinpotentiaalienergiasta ja potentiaalienergiasta kemiallinen energia.

Gravitaatiopotentiaalienergia

Jokaisella esineellä on potentiaalista energiaa, joka perustuu heillään olevan korkeuden suhteen. Tämä yksinkertainen ulkonäön tosiasia kuvaa, koska vesiputous pystyy lisäämään turbiineja ja lopulta muuttuu sähköksi. Esimerkki tässä esitetyistä hiihtäjistä osoittaa myös painon ja korkeuden suhteen gravitaatiopotentiaalienergialla.

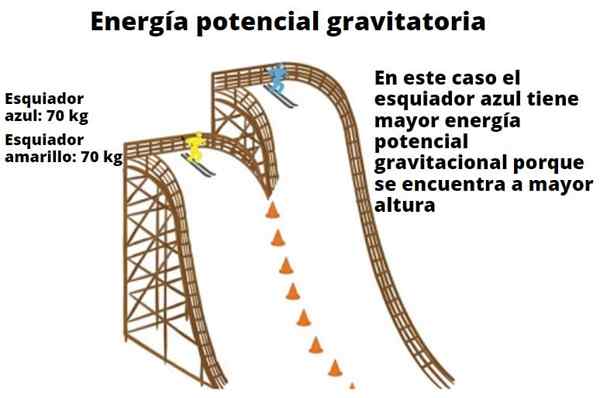
Toinen esimerkki on rulla -vuoristoauto, jolla on suurempi potentiaalienergia, kun se on tietyssä korkeudessa maassa. Kun se on saavuttanut lattian tason, sen korkeus on yhtä suuri kuin nolla ja kaikki sen potentiaalienergia on muutettu kineettiseksi energiaksi (liikeenergia).

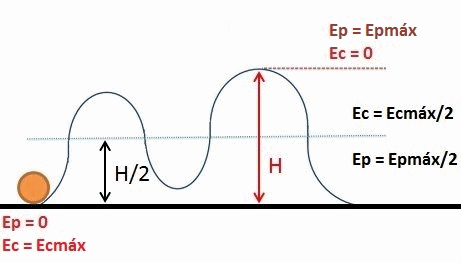Animaatio osoittaa vaihdon gravitaatiopotentiaalienergian ja kineettisen energian, esineen välillä, joka liikkuu vuoristorataan. Molempien energioiden summa, jota kutsutaan mekaaniseksi energiaksi, on vakio koko liikkeen ajan. Lähde: Wikimedia Commons.

Elastinen potentiaalienergia

Esineet, kuten jouset, kaarit, ristikaarit ja liigat, kykenevät varastoimaan joustava potentiaalienergia.

Kun kaaren kireä, maalivahti tekee työn, joka on tallennettu kaari-varustetun järjestelmän potentiaaliseksi energiaksi. Kun kaari vapautuu, tämä energia muuttuu nuolen liikkeeksi. Lähde: Pixabay.

Kehon tai materiaalin joustavuus kuvataan Hooken lailla (tiettyihin rajoihin saakka), mikä kertoo meille, että voima, joka kykenee käyttämään paine tai venytetty, on verrannollinen sen muodonmuutokseen.

Voi palvella sinua: Ferromagnetismi: Materiaalit, sovellukset ja esimerkit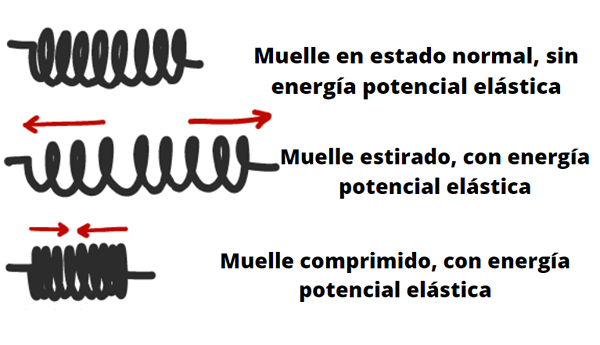

Esimerkiksi jousen tai jousen tapauksessa tämä tarkoittaa, että mitä enemmän se kutistuu tai venyy, sitä suurempi voima, joka voidaan käyttää toiseen päähän asetettuun esineeseen.

Sähköstaattinen potentiaalienergia

Se on energia, joka sähkömaksuilla on kokoonpanossaan. Saman merkin sähkövaraukset hylätään, joten pari positiivista kuormaa - tai negatiivinen - tietyssä asennossa ulkoisen aineen on tehtävä työ. Muuten heillä on taipumus erottaa.

Tämä työ on tallennettu tapaan, jolla kuormat sijaitsivat. Mitä lähemmäksi saman merkin kuormat ovat, sitä suurempi potentiaalienergia on kokoonpano. Se tapahtuu päinvastoin, kun kyse on erilaisista merkkeistä; Kun he houkuttelevat, mitä lähempänä he ovat, sitä vähemmän potentiaalista energiaa heillä on.

Ydinpotentiaalienergia

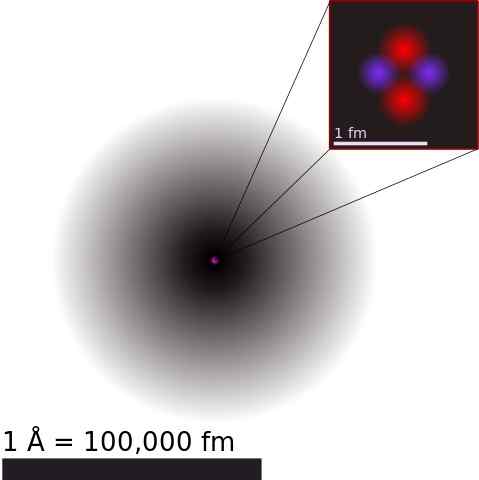Likimääräinen heliumiatomi. Ytimessä protoneja on edustettuna punaisella ja neutronit sinisellä.

Atomi -ydin on koostettu protonit ja neutronit, joita kutsutaan yleisesti Nukleonit. Ensimmäisellä on positiivinen sähkövaraus ja jälkimmäiset ovat neutraaleja.

Koska ne ovat agglomeroituja pienessä tilassa mielikuvituksen ulkopuolella, ja tietäen, että saman merkin kuormat hylätään, on syytä kysyä, kuinka atomiydin pysyy yhtenäisinä.

Vastaus on muissa voimissa sähköstaattisen torjumisen lisäksi, tyypillinen ytimelle, kuten vahva ydinvuorovaikutus ja heikko ydinvuorovaikutus. Nämä ovat erittäin voimakkaita voimia, jotka ylittävät huomattavasti sähköstaattisen voiman.

Kemiallinen potentiaalienergia

Tämä potentiaalienergian muoto johtuu siitä, kuinka atomit ja aineet molekyylejä on saatavana, erityyppisten kemiallisten sidosten mukaan.

Kun kemiallinen reaktio annetaan, tämä energia voidaan muuttaa muun tyyppiksi, esimerkiksi sähköakkulla tai akulla.

Esimerkkejä potentiaalisesta energiasta

Potentiaalista energiaa on läsnä jokapäiväisessä elämässä monilla näkökohdilla. Sen vaikutusten havaitseminen on yhtä helppoa kuin minkä tahansa esineen sijoittaminen tietylle korkeudelle ja sillä on varmuus siitä, että se voi rullata tai pudota milloin tahansa.

Tässä on joitain aiemmin kuvattujen potentiaalisten energiatyyppien ilmenemismuotoja:

-Vuoristoratoja

-Autot tai pallot liikkuvat alamäkeen

-Jouset ja nuolet

-Sähköakut

-Kellon heiluri

Kun yksi äärimmäisistä palloista on käynnissä, liike siirtyy muille. Lähde: Pixabay.

-Keinu

-Hajata

-Käytä sisäänvedettävää kynää.

Katso: Esimerkkejä potentiaalisesta energiasta.

Potentiaalinen energian laskenta

Mahdollinen energia riippuu työstä, joka tekee voimaa, ja tämä puolestaan ​​ei riipu etenemisestä, niin voidaan vahvistaa, että:

-Jos A ja B ovat kaksi pistettä, työ W -_Ab  tarvitaan siirtyä A: sta B: hen, se on yhtä suuri kuin tarvittava työ siirtyä B: stä a. Siksi: W -_Ab = W_Ba, niin:

W -_Ab + W -_Ba = 0

-Ja jos kaksi erilaista suuntausta 1 ja 2 testataan liittymään näihin pisteisiin A ja B, myös molemmissa tapauksissa tehty työ on sama:

 W -₁ = W₂.

Joka tapauksessa esine kokee potentiaalisen energian muutoksen:

Muutos = lopullinen potentiaalienergia - alkuperäinen potentiaalienergia

ΔU = U_lopullinen - TAI_alkukirjain = U_{B -} - TAI_-Lla

No, esineen potentiaalinen energia määritellään voimalla tehdyn työn negatiiviseksi (konservatiivinen):

ΔU = -W_Ab

Mutta koska työ on määritelty tällä integraalilla:

Voi palvella sinua: 31 fysiikan voimantyyppiä ja niiden ominaisuuksia

Missä F ja d -dr - (lihavoidulla tai nuolella) ovat vastaavasti lujuus- ja siirtymävektorit. Tätä silmällä pitäen potentiaalisen energian muutos on tämän integraalin negatiivinen:

Konservatiivisten voimien, kuten kuvatut, integraali lasketaan helposti. 

Huomaa, että potentiaalisen energian yksiköt ovat samat kuin työn. Kansainvälisessä järjestelmässä, jos yksikkö on Joule, joka on lyhennetty ja vastaa 1 Newton X Metro, Englantilainen fyysikko James Joule (1818-1889).

Muita energiayksiköitä ovat Ergio CGS-järjestelmässä, puntahaarko x jalka, BTU (Brittiläinen lämpöyksikkö), kalorit ja kilowatti-hora.

Katsotaanpa joitain tiettyjä tapauksia potentiaalisen energian laskemisesta.

Gravitaatiopotentiaalin energian laskeminen

Maapallon pinnan läheisyydessä painovoimapisteiden voima pystysuoraan ja sen voimakkuus antaa yhtälöllä Paino = massa x painovoima.

Pystysuoran akselin merkitseminen kirjaimella "y" ja osoittamalla tähän osoitteeseen yksikkövektori J -, Positiivinen ja negatiivinen alaspäin, potentiaalisen energian muutos, kun keho siirtyy y = y_-Lla siihen asti kun y = y_{B -} On:

Missä m edustaa kehon vartaloa ja g Painon kiihtyvyyden arvo. Jos sinut valitaan ja_-Lla = 0 referenssitasona maassa, jossa u on kiinteä kuin 0, sinulla on:

U (y) = mgy

Joustavan potentiaalienergian laskeminen

Hooken laki kertoo meille, että voima on verrannollinen muodonmuutokseen:

F = -K.x

Tässä x Se on muodonmuutos ja k -k - Se on jousen vakio, mikä osoittaa kuinka jäykkä se on. Tämän lausekkeen kautta lasketaan elastinen potentiaalienergia ottaen huomioon sen Yllyttää Se on yksikkövektori vaakasuunnassa:

Kun valitaan TAI_-Lla = 0 sisään  x_-Lla, Edellinen lauseke on funktio U (x) Kevään potentiaaliseen energiaan:

U (x) = ½ kx²

Sähköstaattinen potentiaalienergian laskenta

Kun sinulla on täsmällinen sähkövaraus, se tuottaa sähkökentän, joka havaitsee toisen täsmällisen kuorman Q -, Ja mikä toimii sen parissa siirtyessään asemasta toiseen kentän keskellä. Kahden spesifisen kuorman välisellä sähköstaattisella voimalla on säteittäinen suunta, symboloitu yksikkövektorin kautta r --

 Tässä k -k -_ja Se on Coulombin sähköstaattinen tai vakiovakio, jonka arvo on k -k -_ja ≈ 9 x 10⁹  N.m² /C² Kansainvälisissä järjestelmäyksiköissä. Seuraa, että:

 Valitsemalla u = 0, kun r_-Lla → ∞, pysyy:

Ratkaisut

- Harjoitus 1: Sähköinen jousi

Kevät, jonka vakio on k -k - = 10.0 N/cm venyy aluksi 1.00 cm: n tasapainon pituudesta. Pyydetään laskemaan lisäenergia, joka on tarpeen jousen venyttämiseksi 5: een.00 cm sen tasapainon pituuden ulkopuolella.

Ratkaisu 

Korvataan suoraan x = 1.00 cm yhtälössä U (x): lle.cm, mutta senttimetreistä on oltava mittareita energian saamiseksi Joulesissa:

U (1) = 0.5 x 10.0 N/cm x (1.00 cm)² = 5 n. CM = 0.05 J; U (5) = 0.5 x 10.0 N/cm x (5.00 cm)² = 125 n.CM = 1.25 J

Siksi haetun energian ero on 1.25 - 0.05 J = 1.20 J.

- Harjoitus 2: Konservatiiviset ja ei -konservatiiviset voimat

Pieni lohko pisteestä A vapautuu leposta, niin että se liukuu kaarevaa ramppia ilman kitkaa pisteeseen B. Sieltä se tulee pitkään karkeaan vaakasuoraan, dynaamisella kitkakertoimella μ_{k -k -} = 0.2. Löydä mikä etäisyys pisteestä B pysähtyy, olettaen, että H_-Lla= 3M.

Voi palvella sinua: Barrada Spiral Galaxy: muodostuminen, kehitys, ominaisuudet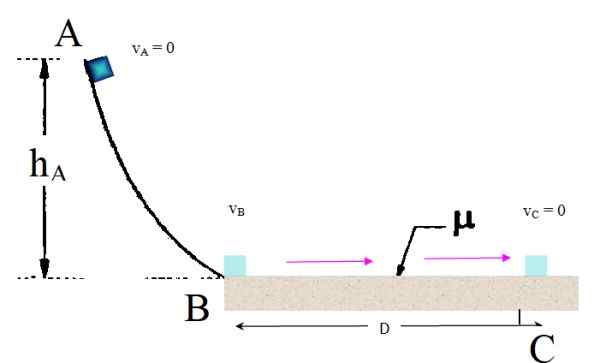Kuva esimerkiksi 1. Lähde: f. Zapata.

Ratkaisu 

Kun lohko on korkeudessa H_-Lla Lattian suhteen sillä on gravitaatiopotentiaalienergia korkeudestaan. Päästäessä irti, tästä potentiaalisesta energiasta tulee vähitellen kineettinen energia, ja kun se liukuu sileän kaarevaan rampin läpi, sen nopeus kasvaa.

Matkan A: sta B: hen B: n tasaisesti vaihtelevan suoraviivaisen liikkeen yhtälöitä ei voida käyttää. Vaikka painovoima on vastuussa lohkon liikkeestä, tämä kokee, että tämä kokee on monimutkaisempi, koska etenemissuunta ei ole suoraviivainen.

Energiansäästö AB -reitillä

Koska painovoima on konservatiivinen voima ja rampissa ei ole kitkaa, mekaanisen energian säilyttämistä voidaan käyttää nopeuden löytämiseen, kun se saavuttaa rampin lopun:

Mekaaninen energia a = mekaaninen energia B: ssä

m.g.h_-Lla + ½ m.v_-Lla² = m.g.h_{B -} + ½ m.v_{B -}²

Lauseketta yksinkertaistetaan huomaamalla, että massa näkyy jokaisessa termissä. Julkaistaan ​​leposta V_-Lla = 0. Ja h_{B -} Se on maanpinnan tasolla, h_{B -} = 0. Näillä yksinkertaistuksilla lauseke pelkistetään:

v_{B -}² = GH_-Lla

Työt tehdään hankaamalla osassa eKr

Nyt lohko aloittaa reitin karkeassa osassa tällä nopeudella ja lopulta pysähtyy kohtaan C. Siksi v_C = 0. Mekaanista energiaa ei enää säilytetä, koska kitka on hajoava voima, joka on tehnyt työn:

W -_kosketus = -Käyttö x -matkan ajomatkan päässä

Tällä työllä on negatiivinen merkki, koska kineettinen kitka hidastuu esineeseen vastustaen sen liikettä. Kineettisen kitkan suuruus F_{k -k -}  On:

F_{k -k -} = μ_{k -k -} .N

Missä n on normaalin voiman suuruus. Normaalin voiman pinta kohdistaa lohkon pinnan, ja koska pinta on täysin vaakasuora, koska se tasapainottaa painoa P = mg, Siksi normaalin suuruus on:

N = mg

Mikä johtaa:

F_{k -k -} = μ_{k -k -} .mg

Työ F_{k -k -} Tekee lohko on: W -_{k -k -} = - f_{k -k -} .D =- μ_{k -k -} .mg.D -d.

Mekaanisen energian muutoksen laskeminen

Tämä työ vastaa mekaanisen energian muutosta, joka on laskettu näin:

Mekaaninen energia C - mekaanisessa energiassa kohdassa b =

ΔE_m = (U_C +K -k -_C)- (tai_{B -} + K -k -_{B -}) = - μ_{k -k -} .mg.D -d

Tässä yhtälössä on joitain termejä, jotka on kumottu: k_C = 0, koska lohko pysähtyy C: ssä ja se on myös muokattu u_C = U_{B -}, Näiden pisteiden olemisesta maanpinnan tasolla. Yksinkertaistaminen johtaa:

- K -k -_{B -} = - μ_{k -k -} .m.g.D -d

½ m.v_{B -}² = μ_{k -k -} .m.g.D -d

Taikina peruutetaan uudelleen ja se voidaan saada seuraavasti:

D = (½ V_{B -}²)/(μ_{k -k -} . G) = (½ V_{B -}²)/(μ_{k -k -} . g) = (½ g.h_-Lla)/(μ_{k -k -} . g) = (½h_-Lla)/μ_{k -k -} = 0.5 x 3 m / 0.2 = 7.5m

Viitteet

1. Bauer, W. 2011. Fysiikka tekniikkaan ja tieteisiin. Osa 1. MC Graw Hill.
2. Figueroa, D. (2005). Sarja: Tieteen ja tekniikan fysiikka. Nide 2. Dynaaminen. Toimittanut Douglas Figueroa (USB).
3. Giancoli, D.  2006. Fysiikka: sovellusten periaatteet. Kuudes. Ed Prentice Hall.
4. Ritari, r.  2017. Tutkijoiden fysiikka ja tekniikka: strategialähestymistapa. Pearson. 
5. Sears, Zemansky. 2016. Yliopiston fysiikka, jolla on moderni fysiikka. 14. päivä. Ed. Nide 1-2.