Käännöstasapainoolosuhteet, esimerkit, harjoitukset

Sanotaan, että esine on Käännöstasapaino Kun häneen käyttävien joukkojen summa on nolla. Tämä ei tarkoita, että loput on välttämättä, mutta liike, jos se on olemassa.

Mekaaniset tasapainoolosuhteet perustuvat Newtonin mekaniikkalakeihin. Itse asiassa ensimmäinen laki kertoo meille, että esine on levossa tai liikkuessa yhtenäisen suorakulmaisen liikkeen MRU: lla, edellyttäen, että mikään nettovoima ei toimi siihen.

Tämä lamppu on käännöstasapaino

Nyt tuloksena oleva nettovoima tai voima on yksinkertaisesti kaikkien esineeseen vaikuttavien voimien vektorisumma. Newtonin toisen lain mukaan tämän summan on oltava yhtä suuri kuin massan ja kiihtyvyyden välinen tuote, mutta jos kohdetta ei kiihdytetä, tämä summa on kumota.

Ja koska kiihtyvyyttä ei ole kaksi mainitun mahdollisuuden: ruumis on levossa, ts. Se ei liiku, tai jos se tapahtuu, sen on oltava MRU: n kanssa. Ensimmäisessä tapauksessa puhutaan staattisesta rajat ylittävästä tasapainosta ja toisessa dynaamisesta.

Käännöstasapaino on tärkeä tekijä monissa tekniikan näkökohdissa, esimerkiksi rakentamisessa. Rakennuksen muodostavien elementtien: palkit, kaapelit, kehykset ja muut on oltava tasapainossa kotelon vakauden takaamiseksi.

Translaatiotasapaino etsitä.

[TOC]

Käännöstasapaino

Oletetaan, F₁, F₂, F₃.. . F_n, käyttämällä rohkeaa kirjettä korostaa sitä tosiasiaa, että voimat ovat vektoreita ja että ne on lisättävä sellaisenaan.

Kaikkien näiden voimien vektorisummaa kutsutaan tuloksena oleva voima jompikumpi Nettovoima. Jos tämä summaus johtaa nollavektoriin, käännöstasapainon ehto täyttyy:

Voi palvella sinua: suljettu sähköpiiri

F₁+ F₂+ F₃.. .+ F_n = 0 -

Tämä ehto voidaan kirjoittaa tiiviisti summaus:

∑ F_Yllyttää = 0 -

Tuloksena olevan voiman komponenttien suhteen aikaisempi yhtälö, joka on vektori, voidaan jakaa kolmeen skalaariyhtälöön, yksi tuloksena olevan voiman jokaiselle komponentille:

∑ f_Ix = 0; ∑ f_ja = 0 ja ∑ f_{z -z} = 0

Käytännössä se ei ole helppoa.

Tästä syystä todelliset esineet eivät melkein koskaan vapauteta ulkoisista voimista, ja seurauksena on vaikea saada käännöstasapaino.

Joten insinöörit käyttävät mekanismeja hieromisen vähentämiseen, kuten laakerit ja voiteluaineöljyjen käyttö.

Vapaat kehon kaaviot

Vapaa kehon kaavio on kaavio, jossa kehon kohdalla olevat voimat vedetään. Kun käännöstasapaino etsitään, nämä voimat on oltava tasapainossa. Esimerkiksi, jos käytät alaspäin suuntautuvaa pystysuuntaista voimaa, kuten paino, niin on oltava pystysuuntainen voima, jolla on täsmälleen sama suuruus.

Tämä voima voidaan antaa käsityölle, joka kestää esineen niin, että se ei pudota, köyttä tai yksinkertaisesti pöydän pintaa.

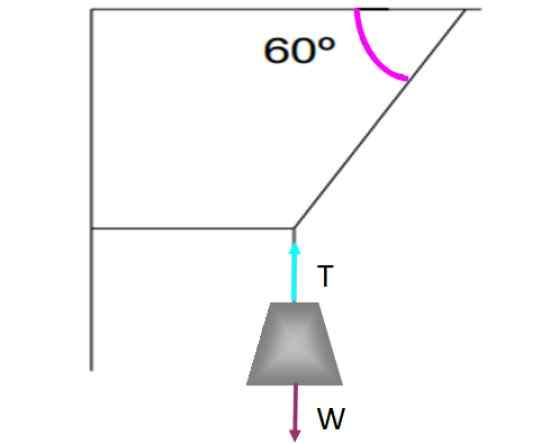
Jos pinnalle on tangentiaalinen voima, kuten kineettinen tai staattinen kitka, on oltava toinen vastakkainen voima siten, että tasapaino on olemassa. Tarkkailemme esimerkiksi painoa, joka roikkuu seuraavassa kuvassa esitetyistä jousista.

Esimerkki esineestä, joka on käännöstasapainossa. Lähde: f. Zapata.

Paino pysyy käännöksen tasapainossa ja liikkumatta sitä pitävän pystysuoran köyden ansiosta harjoittamalla jännitystä T joka kompensoi painoa W -. Jokainen voima on esitetty lännessä nuolen, jokaisen koon ja samaan suuntaan, mutta vastakkaiseen suuntaan.

Voi palvella sinua: isobarinen prosessi: kaavat, yhtälöt, kokeet, harjoitukset

Tasapainotusvoima

Oletetaan, että joukko voimia toimii esineeseen. Tätä kutsutaan a joukkojen järjestelmä joista tuloksena voidaan löytää edellä selitetyllä tavalla: Jokaisen järjestelmän lisääminen vektorisesti.

No, tätä tulosta vastapäätä olevaa voimaa kutsutaan tasapainotusvoima. Jos tuloksena oleva voima on F_{R -} Ja tasapainotusvoima on JA, niin:

JA + F_{R -} = 0

Siksi:

JA = - F_{R -}

Käännös tasapainotesimerkit

Monet esineet, jotka löydämme päivittäin, sisältä ja kodista, ovat käännöstasapainossa:

Rakennukset ja tiet

Rakennukset ja tiet on rakennettu pysymään vakaana eivätkä käänny tai romahta. Pilvenpiirtäjissä ja yleensä erittäin korkeissa rakennuksissa on kuitenkin tarpeen joustavuutta tuulen vaikutuksen kestämiseksi.

Kirjat ja esineet hyllyillä

Kirjaston kirjat ja myymälöiden tuotteet ovat esineitä, jotka pysyvät käännöstasapainossa ja liikkumatta.

Huonekalut

Huonekalut, taulutelevisio ja seinän maalaukset sekä katosta roikkuvat lamput mainitaksesi joitain esineitä, ovat käännöstasapainossa.

Liikennevalot

Liikennevalot kiinnitetään pylväät ja kaapelit, jotta ne eivät pudota. Tiedämme kuitenkin, että tuuli saa ne värähtelemään.

Julkinen valaistus

Julkiset valaistusvalot ovat myös käännöstasapainossa, kiinnitetään kevyisiin viesteihin, kuten pääkuvan pääkuva.

Liikuntaa

Minkä voimakkuuden pitäisi olla F_s Staattinen kitka, jotta kuvion laatikko pysyy levossa kaltevan tason keskellä kulma α 37º? Laatikon massa on m = 8 kg.

Voi palvella sinua: API Gravity: Scale and luokittelu raakaöljyn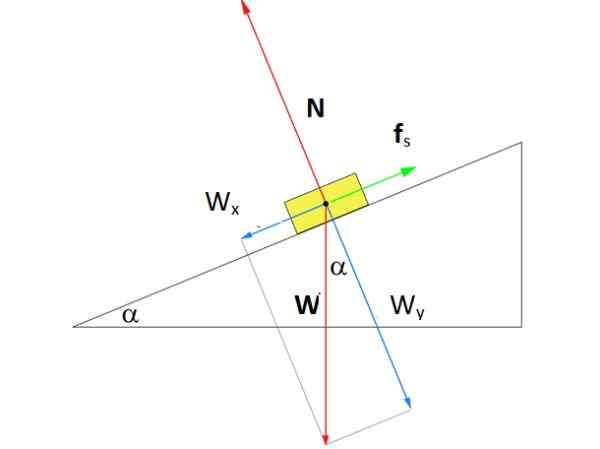Vapaa runkokaavio lepoharjalle kaltevalla tasolla. Lähde: f. Zapata.

Ratkaisu

Kuva näyttää lentokoneen vapaan rungon kaavion. Häneen on kolme voimaa: paino W -, Pystysuoraan suunnattu, normaali N, joka on kohtisuora voima, jonka tason pinta kohdistaa laatikon yli, ja lopulta staattinen kitkavoima F_s Se vastustaa laatikkoa liukumaan alamäkeen.

Käännöstasapainon ehto osoittaa, että:

W - + N + F_s = 0 -

Mutta sinun on muistettava, että tämä on vektorisumma, ja sen toteuttamiseksi on tarpeen hajottaa voimat komponenteiksi koordinaattiakseleilla.

Kuvassa on piirretty koordinaattijärjestelmä. Tällä valinnalla staattinen kitka putoaa tälle akselille, kun taas normaali on akselilla ja. Paino on ainoa kalteva voima ja meidän on hajotettava trigonometrian avulla:

W -_x = W. synti α
W -_ja = W. cos α

Jokaisen akselin voimien summa on:

∑ f_ja = N - w_ja = 0
∑ f_x = f_s - W -_x = 0

Tästä viimeisestä yhtälöstä seuraa, että:

F_s = W_x

Ja kuten w_x = W. sin α ja painon suuruus vuorotellen on w = m.G, G -painovoiman arvo, joten staattisen kosketuksen suuruus on yksinkertaisesti:

F_s = m⋅g⋅sen α = 8 kg × 9.8 m/s² × Sen 37º = 47.2 n.

Viitteet

1. Bauer, W. 2011. Fysiikka tekniikkaan ja tieteisiin. Osa 1. MC Graw Hill.
2. Figueroa, D. (2005). Sarja: Tieteen ja tekniikan fysiikka. Nide 2. Dynaaminen. Toimittanut Douglas Figueroa (USB).
3. Giambattista, a. 2010. Fysiikka. Toinen. Ed. McGraw Hill.
4. Serway, R., Jewett, J. (2008). Fysiikka tieteen ja tekniikan fysiikka. Osa 1. 7^mehu. Ed. Cengage -oppiminen.
5. Tippens, P. 2011. Fysiikka: Käsitteet ja sovellukset. 7. painos. McGraw Hill.