Translaation tasapainon määrittäminen, sovellukset, esimerkit

Hän Translaatiotasapaino Se on tila, jossa esine kokonaisuutena on, kun kaikki siihen vaikuttavat voimat kompensoivat, mikä johtaa tyhjään voimaan. Matemaattisesti se vastaa sanomista, että f₁+ F₂ +  F₃ +.. . = 0, F -f₁, F₂,  F₃... mukana olevat voimat.

Se tosiasia, että ruumis on translaatiotasapainossa, ei tarkoita, että se on välttämättä levossa. Tämä on erityinen edellisen määritelmän tapaus. Kohde voi olla liikkeessä, mutta kiihtyvyyden puuttuessa tämä on yhtenäinen suorakulmainen liike.

Kuvio 1. Käännöstasapaino on tärkeä monille urheilulajeille. Lähde: Pixabay.

Joten jos vartalo on levossa, jatkuu. Ja jos sinulla on jo liikettä, sillä on jatkuva nopeus. Minkä tahansa esineen liikkuminen on yleensä käännösten ja kiertojen koostumus. Käännökset voivat olla kuvan 2 mukaisesti: lineaarinen tai kaareva.

Mutta jos yksi esineen pisteistä on kiinteä, niin ainoa liikkumismahdollisuus on kiertää. Esimerkki tästä on CD, jonka keskus on kiinteä. CD: llä on mahdollisuus kiertää akselin ympäri, joka kulkee sen pisteen läpi, mutta ei liikkua.

Kun esineissä on kiinteitä pisteitä tai niitä tuetaan pinnoilla, puhutaan linkit. Linkit ovat vuorovaikutuksessa rajoittaen liikkeitä, joita esine pystyy tekemään.

[TOC]

Translaatiotasapainon määrittäminen

Tasapainossa olevalle hiukkaselle on pätevä varmistaa, että:

F_{R -} = 0

Tai yhteenvetomerkinnässä:

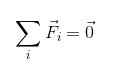
On selvää, että kehon on translaatiotasapaino, sen kanssa toimivat voimat on jollain tavalla kompensoida, joten sen tulos on mitätön.

Tällä tavoin objekti ei koe kiihtyvyyttä ja kaikki sen hiukkaset ovat levossa tai kokeilemassa suoran sisäisiä käännöksiä vakiona nopeudella.

Se voi palvella sinua: Big Bang -teoria: Ominaisuudet, vaiheet, todisteet, ongelmat

Nyt, jos esineet voivat kääntyä, ne yleensä tekevät sen. Siksi suurin osa liikkeistä koostuu käännös- ja kiertoyhdistelmistä.

Esineen kierto

Kun kiertotasapaino on tärkeä, voi olla tarpeen varmistaa, että esine ei käänny. Sitten sinun on tutkittava, onko siihen toimivia vääntöjä vai hetkiä.

Vääntömomentti on vektorin suuruus, josta kierto riippuu. Vaatii voimaa, mutta tämän soveltamispiste on myös tärkeä. Idean selventämiseksi harkitse laajennettua kohdetta, jolla voima toimii F Ja katsotaanpa, pystytkö tuottamaan pyörimisen jonkin akselin tai.

On jo intuoitu, että työntämällä esine pisteeseen P voiman kanssa F, On mahdollista kääntää piste O, anti -Horary -suunnassa. Mutta suunta, johon voimaa käytetään, on myös tärkeä. Esimerkiksi väliaineen kuvassa käytetty voima ei pysty kääntämään objektia, vaikka se voi varmasti siirtää sitä.

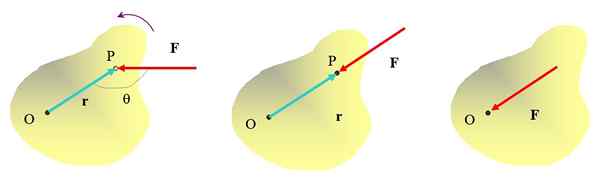Kuva 2. Saadaan erilaisia ​​tapoja käyttää voimaa laajalle esineelle, vain äärimmäisen vasemmanpuoleisen kuvion yhteydessä saadaan kiertovaikutus. Lähde: Itse tehty.

Käytä voimaa suoraan pisteeseen tai sitä ei myöskään käytetä esineen kääntämiseen. Sitten on selvää, että pyörimisvaikutuksen saavuttamiseksi voima on kohdistettava tietylle etäisyydelle pyörimisakselista ja sen toimintalinja ei saisi mennä kyseisen akselin läpi.

Määritelmä vääntömomentti

Voiman vääntömomentti tai momentti, joka on merkitty τ: ksi vektorien suuruus, joka vastaa kaikkien näiden tosiasioiden yhdistämisestä, määritellään seuraavasti:

τ = r x f

Vektori r - Se on suunnattu kierto -akselista voiman levityspisteeseen ja R: n ja F: n välisen kulman osallistuminen on tärkeää. Siksi vääntömomentin suuruus ilmaistaan ​​seuraavasti:

Voi palvella sinua: Newtonin ensimmäinen laki: kaavat, kokeet ja harjoitukset

τ = r.F.Senttiä Q -

Tehokkain vääntömomentti tapahtuu, kun r - ja F Ne ovat kohtisuorassa.

Nyt, jos toivotaan, että kiertoa ei ole tai nämä kulkevat jatkuvalla kulmaki

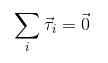
Tasapainoolosuhteet

Tasapaino tarkoittaa vakautta, harmoniaa ja tasapainoa. Jotta objektin liikkuminen hallitsee näitä ominaisuuksia, on sovellettava edellisissä osissa kuvattuja olosuhteita:

1) f₁+ F₂ +  F₃ +.. . = 0

2) τ₁+ τ₂ +  τ₃ +.. . = 0

Ensimmäinen ehto takaa translaatiotasapainon ja toisen kiertokyvyn. Molemmat on täytettävä, jos esineen halutaan jäädä staattinen saldo (kaikenlaisen liikkeen puuttuminen).

Sovellukset

Tasapainoolosuhteet voidaan soveltaa lukuisiin rakenteisiin, koska kun rakennukset tai monimuotoiset esineet on rakennettu, se tehdään tarkoituksella. Toisin sanoen, että objektia ei ole aseistettu.

Tämä on tärkeää esimerkiksi rakennettaessa siltoja, jotka pysyvät tiukasti jalkojensa alla, tai suunnitellessasi asuttavia rakenteita, jotka eivät muuta asemaa tai joilla on taipumus tyhjentää.

Vaikka uskotaan, että tasainen suorastettua liike on äärimmäinen liikkeen yksinkertaistaminen, jota yleensä esiintyy luonteeltaan vähän, on muistettava, että tyhjyyden valon nopeus on vakio ja myös ilmassa olevan äänen, jos myös ilmassa pitää ympäristön homogeenista.

Monissa ihmisen tekemissä mobiilirakenteissa on tärkeää, että ylläpidetään jatkuvaa nopeutta: esimerkiksi mekaanisilla portailla ja kokoonpanolinjoilla.

Se voi palvella sinua: termodynamiikan toinen laki: kaavat, yhtälöt, esimerkit

Translaatiotasapainotesimerkit

Tämä on klassinen jännitteiden harjoitus, joka pitää lampun tasapainossa. On tiedossa, että lamppu painaa 15 kg. Löydä tarvittavien jännitteiden suuruus pitämään se tässä asennossa.

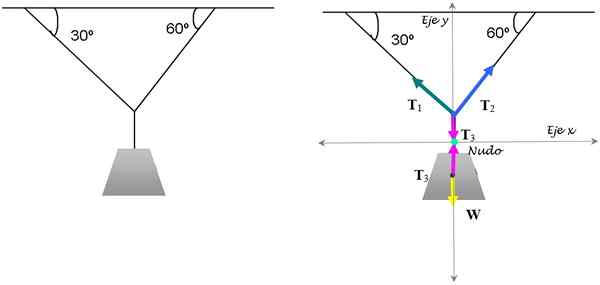Kuva 3. Lampun saldo taataan soveltamalla translaatiotasoa. Lähde: Itse tehty.

Ratkaisu

Sen ratkaisemiseksi keskitymme solmuun, jossa kolme merkkijonoa yhdistyvät. Kunnossa ja lampun vastaavat vapaat rungon kaaviot on esitetty yllä olevassa kuvassa.

Lampun paino on W = 5 kg . 9.8 m/s² = 49 n. Jotta lamppu olisi tasapainossa, riittää, että ensimmäinen tasapainoolosuhde täyttyy:

T₃ - W = 0

T₃ = W = 49 n.

Jännitteet T₁ ja T₂ Niiden on hajotettava:

T_1y + T_{2 ja} - T₃ = 0 (Voimien kesä Y -akselia pitkin))

-T_1x +T_2x = 0 (Voimien kesä X -akselia pitkin)

Trigonometrian soveltaminen:

T₁.Cos 60º +t₂ .Cos 30º = 49

- T₁.SEN60º +T₂.SEN30º = 0

Se on kahden yhtälön järjestelmä, jossa on kaksi tuntematonta, jonka vastaus on: T₁ = 24.5 n ja T₂ = 42.4 n.

Viitteet

1. Rex, a. 2011. Fysiikan perusteet. Pearson. 76 - 90.
2. Serway, R., Jewett, J. (2008). Fysiikka tieteen ja tekniikan fysiikka. Osa 1. 7^mehu. Ed. Cengage -oppiminen. 120 - 124.
3. Serway, R., ULOLE, c. 2011. Fysiikan perusteet. 9^naa Ed. Cengage -oppiminen. 99-112.
4. Tippens, P. 2011. Fysiikka: Käsitteet ja sovellukset. 7. painos. MacGraw Hill. 71 - 87.
5. Walker, J. 2010. Fysiikka. Addison Wesley. 332 -346.