Kiertotasapainon kaavat ja yhtälöt, esimerkit, harjoitukset

Väitetään, että laajennettu elin on kiertotasapaino Kun sen kanssa toimivien vääntömomenttien summa on nolla. Tämä ei tarkoita, että esine on välttämättä levossa, vaan pikemminkin, että sen liikkumistilan muuttamiseksi toiseen ei ole verkkotrendiä.

Kohde, joka liikkuu vakiona nopeudella, tekee niin suoraa linjaa pitkin ja voimme harkita sitä kiertotasapainossa. Nyt esineet pyörivät, koska on voimia, jotka vaikuttavat niihin siten, että se on kierto. Voiman kyky tuottaa kiertoa, nimeltään vääntömomentti tai Torca, Se ei riipu pelkästään voiman voimakkuudesta, vaan myös missä sitä käytetään.

Kuvio 1. Kuvion jousitussilta suunniteltiin kiertämisen tasapainossa. Lähde: Wikimedia Commons.

Tunnustamme tämän heti, kun suljettu ovi aukeaa: voimaa ei koskaan kohdisteta saranoiden lähellä, vaan kaukana niistä, joten kahva on sijoitettu niin pitkälle kuin mahdollista, oven oven viereen.

Saranat ohittavat oven kierto -akselin. Vaatiessasi työntää sitä hyvin lähellä saranoja, sinun on ponnisteltava oven kanssa edes liikkuaksesi vähän.

Kirjallisuudessa on vääntömomentti, jolla on erilaiset nimet: vääntö, vääntö, voima- ja Torca -hetki. Kaikki ovat synonyymejä.

Joten meidän on tiedettävä vääntömomentit, jotka toimivat objektille kiertotasapainon olosuhteiden luomiseksi.

[TOC]

Kiertotasapaino

Kiertotasapainon olosuhde on:

Kaikkien akselien suhteen laskettujen momenttien tai vääntömomenttien summa on mitätön.

Kyseistä kohdetta on laajennettava, koska hiukkasilla on määritelmän mukaan vain käännöstasapaino.

Voit palvella sinua: Newtonin toinen laki: sovellukset, kokeet ja harjoitukset

Kehoon voidaan kohdistaa voimia ja kiertotasapaino on edelleen, kun taas voimat eivät käännä sitä.

Siellä voi olla myös liikettä, jopa kiihdytetty, mutta aina suoraa linjaa pitkin, koska kaikki voimat eivät aiheuta vääntömomenttien ulkonäköä. Nämä ilmestyvät, kun joukot eivät toimi koko toimintalinjalla.

Vääntömomentti tai voimamomentti

Vääntömomentti on merkitty kreikkalaisten lyrics τ, sisään lihavoitu kirjasin Koska se on vektori ja erotamme sen sen suuruudesta tai moduulista, joka on skalaari. Se riippuu käytetystä voimasta F, vektori r - joka on suunnattu kierto -akselista tai voiman levittämispisteeseen ja lopuksi näiden kahden vektorin välisestä kulmasta.

Näiden suuruuksien välinen oikea suhde vahvistetaan vektorituotteen kautta:

τ = r x F

Ja vääntömomentin moduuli, joka on merkitty ilman lihavointia, on:

τ = r⋅f⋅sen θ

Missä θ on kulma r - ja F. Vääntömomenttiyksiköt ovat yksinkertaisesti N⋅m kansainvälisessä järjestelmässä.

Kuvassa on englanninkielinen avain, jonka kanssa se on tarkoitettu. Tätä varten kaksi voimaa kokeetaan F_-Lla ja F_{B -}.

F_-Lla on lähempänä O: ta ja sillä on vektori r -_-Lla tai lyhyempi vipuvarsi, siksi ei tuota niin paljon vääntömomenttia ja voimaa F_{B -}, Sillä on sama suuruus, mutta sillä on vektori r -_{B -} suurempi.

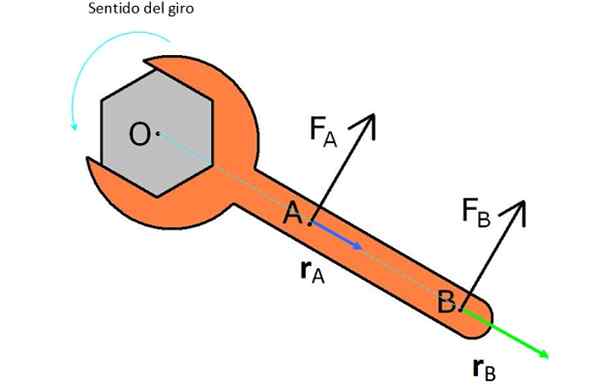Kuva 2. Englanninkieliseen avaimeen kohdistetut voimat ja aseet kääntääkseen sen kello -neulojen vastaisesti. Lähde: Wikimedia Commons.

Huomaa, että jos haluat kiertää mutteria aikataulussa, sinun on kohdistettava voimia vastakkaiseen suuntaan kuin ne ilmestyvät kuvaan.

Vääntömomentin suunta ja tunne

Kun vääntömomentti johtuu ristiintuotteesta lujuus- ja sijaintivektoreiden välillä, ja nämä ovat englanninkielisen avaimen tasossa, vääntömomentin on oltava vektori, joka on kohtisuorassa siihen tasoon nähden, toisin sanoen lukijalle tai sivun sisäpuolelle.

Voi palvella sinua: Ilmakehän paine: Normaali arvo, miten se mitataan, esimerkkejä

Yleissopimuksen mukaan vääntömomentti on positiivinen, jos se tuottaa käännöksen kelloneulojen vastakkaiseen suuntaan, ja negatiivinen, jos se tekee niin kellon suuntaan.

Tuloksena olevan vääntömomentin suunta ja suunta määritetään helposti alla esitetyn oikean käden säännön perusteella:

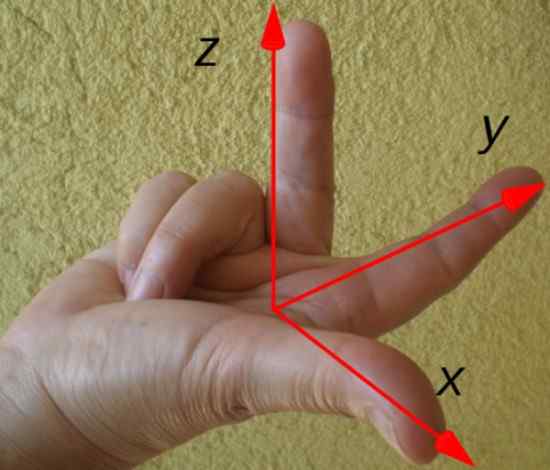Kuva 3. Oikeanpuoleinen sääntö trokan suunnan ja suunnan määrittämiseksi. Lähde: Wikimedia Commons.

Etusormenpisteet sijaintivektorin mukaan r -, Keskisormi voiman mukaan F Ja peukalo merkitsee vääntömomentin suuntaa ja suuntaa τ. Tässä esimerkissä vääntömomentti on suunnattu X -akselia pitkin, koordinaattiakselien piirtämisen mukaan.

Kaavat ja yhtälöt

Jos vääntömomentit toimivat vartaloon τ₁, τ_2, τ_3… τ_Yllyttää, Verkko tai tuloksena oleva vääntömomentti τ_n Se on kaikkien vektorisumma:

τ_n = τ₁+ τ₂ +  τ₃ +_.. τ_Yllyttää

Yhteenveto summauksen myötä se on edelleen:

τ_n = ∑ τ_Yllyttää

Tasapainotila ilmaistaan ​​matemaattisesti seuraavasti:

τ_n = 0 -

O No:

∑ τ_Yllyttää = 0 -

Missä vääntömomentti τ, Tietyn O -akselin suhteen se lasketaan:

τ = r x F

Ja kenen suuruus on:

τ = r⋅f⋅sen θ

Esimerkit

-Ihmisillä ja eläimillä paino on voima, joka voi aiheuttaa vääntömomentin ja kääntyä ja pudota.

Ihmiset ylläpitävät yleensä sellaista asemaa, että kävellessään pitävät heidät kiertotasapainossa, ellei urheilua harjoiteta, kuten voimistelu, luistelu tai urheilu yleensä.

-Kaksi lasta, jotka onnistuivat pysymään vaakasuorassa rokkari jompikumpi ylös ja alas Ne ovat kiertotasapainossa.

-Kun tasapainon lautaset ovat tasapainossa, järjestelmä on pyörimis tasapainossa.

-Kaduilla ja keinoilla roikkuvat ilmoitukset ja liikennevalot ovat myös kiertotasapainossa. Jos niitä pitävät kaapelit ovat rikki, tämä tasapaino on menetetty ja ilmoitus roikkuu tai putoaa.

Se voi palvella sinua: keskimääräinen kiihtyvyys: miten se lasketaan ja ratkaistaan

-Ripustavat sillat, kuten kultainen portti San Franciscossa ja kuvan 1 silta.

Liikuntaa

Kuvassa esitetyn tuen tukemaa palkkia on erittäin kevyt. Tuen aiheuttama voima on F Ja lopussa voima koskee -Lla.

Näiden voimien suuruudet pyydetään laskemaan, kun otetaan huomioon, että järjestelmä on kääntämisen ja kierto tasapainossa.

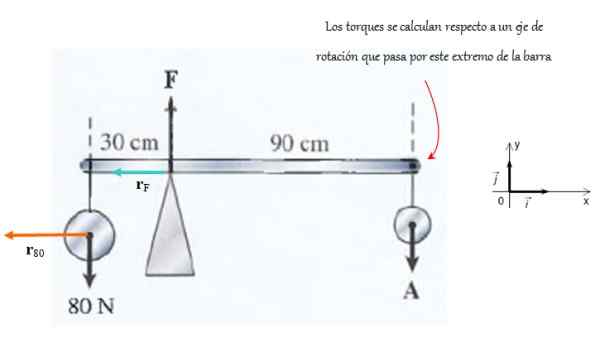Kuva 4. Tällä palkilla voimat toimivat siten, että se pysyy kierto -tasapainossa. Lähde: f. Zapata.

Ratkaisu

Koska järjestelmä ei liiku, voimien summa peruutetaan. Kaikki ovat pystysuoria ja voit työskennellä suuruuksien kanssa. Positiivinen merkitys on ylös ja negatiivinen, siksi:

F - 80 - a = 0

Nyt sovelletaan pyörimis tasapainolehtoa, jolle sinun on valittava mielivaltainen kierto -akseli. Tässä tapauksessa se valitaan oikeassa lopussa, niin että vektori r -_-Lla Ole tyhjä, tällä tavalla vääntömomentti -Lla, Mutta vain ne F ja vasemman vahvuus.

Tuotettu vääntömomentti F Se on oikean käden säännön ja esitetyn koordinaattijärjestelmän mukaan:

τ_F = r -_F x F = 0.9 F (-k -k -) N.m

Se on suunnattu näytölle ja sillä on negatiivinen merkki. Vaikka 80 N: n voiman tuottama vääntömomentti on:

τ = 80 x 1.kaksikymmentä (k -k -) N⋅m = 96 (k -k -) N⋅m

Tämä vääntömomentti on suunnattu ulos näytöltä ja siihen on annettu positiivinen merkki. Koska kiertotasapaino on:

96 - 0.9⋅f = 0

Suuruus F On:

F = (96/0.9) n = 106.7 n

Ja koska järjestelmä on käännöstasapainossa, voimien summa peruutetaan. Tämän avulla voimme tyhjentää suuruuden -Lla-

F - A - 80 n = 0

Siksi:

A = 106.7 - 80 N = 26.7 n.

Viitteet

1. Rex, a. 2011. Fysiikan perusteet. Pearson.
2. Serway, R., Jewett, J. (2008). Fysiikka tieteen ja tekniikan fysiikka. Osa 1. Seitsemäs. Ed. Cengage -oppiminen.
3. Sears, Zemansky. 2016. Yliopiston fysiikka, jolla on moderni fysiikka. 14. päivä. Ed. Osa 1. Pearson.
4. Tipler, P. (2006) Tieteen ja tekniikan fysiikka. 5. ed. Osa 1. Toimitus palautti.
5. Tippens, P. 2011. Fysiikka: Käsitteet ja sovellukset. 7. painos. McGraw Hill.