Matematiikka

Näytteenottovirhekaavut ja yhtälöt, laskenta, esimerkit

Näytteenottovirhekaavut ja yhtälöt, laskenta, esimerkit

Hän näytteenottovirhe jompikumpi näytevirhe Tilastoissa on eroa näytteen keskiarvon välillä kokonaispopulaation keskiarvon suhteen. Kuvittelemme ajatusta, että kaupungin kokonaisväestö on miljoona, josta haluat sen keskimääräiset kengät, joista tuhannet ihmiset otetaan satunnaisesti näytteessä.

Otosta johtuva keskimääräinen koko ei välttämättä vastaa kokonaispopulaation kokoa, vaikka näytteessä ei ole puolueellista, arvon on oltava lähellä. Tämä ero näytteen keskiarvon ja kokonaispopulaation välillä on näytevirhe.

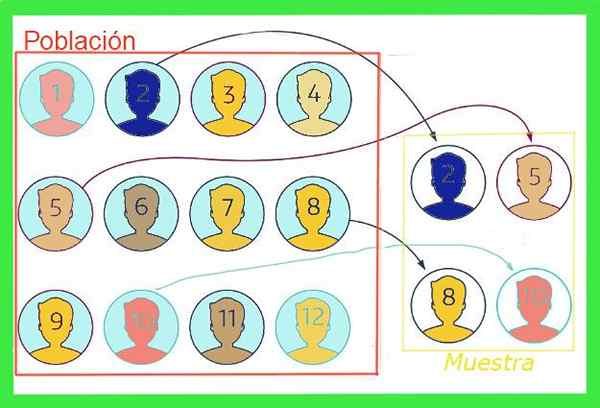
Kuvio 1. Koska otos on kokonaispopulaation osajoukko, näytteen keskiarvo on virhemarginaali. Lähde: f. Zapata.

Yleensä koko väestön keskiarvoa ei tunneta, mutta tällaisen virheen ja kaavojen vähentämiseksi on tekniikoita arvioida Näytevirhemarginaali Se esitetään tässä artikkelissa.

[TOC]

Kaavat ja yhtälöt

Annetaan, että haluat tietää tietyn mitattavan ominaisuuden keskiarvon x Koolaisessa väestössä N, mutta miten N Koko väestön tutkiminen ei ole suuri määrä, joten jatkamme a aleaarinen näyte kooltaan n<.

Näytteen keskiarvo on merkitty ja koko väestön keskiarvo merkitsee sitä kreikkalaiselle kirjaimelle μ (Se lukee Mu tai miu-A.

Oletetaan, että ne otetaan m Väestön kokonaisnäytteet N, Kaiken yhtä suuri n Keskimääräiset arvot 1-, 2-, 3>, .. .m-.

Nämä keskiarvot eivät ole identtisiä keskenään ja ovat kaikki keskimääräistä populaation arvoa μ. Hän Näytevirhemarginaali E osoittaa keskiarvojen odotetun eron suhteessa Keskimääräinen populaation arvo μ määritetyn prosentin sisällä nimeltään Luottamustaso γ (Gamma-A.

Voi palvella sinua: lisäaine käänteinen

Hän Vakiovirhemarginaali ε koko näyte n On:

ε = σ/√n

missä σ on keskihajonta (Varianssin neliöjuuri), joka lasketaan seuraavalla kaavalla:

σ = √ [(x -)2/(N - 1)]

Tarkoitus Vakiovirhemarginaali ε on seuraava:

Hän keskiarvo saatu koonäytteellä n ymmärretään aikavälillä ( - ε, + ε) kanssa luottamustaso 68,3%.

Kuinka laskea näytteenottovirhe

Edellisessä osassa annettiin kaava virhealue standardi N -näytteestä, jossa vakiosana osoittaa, että se on virhemarginaali, jolla on 68%.

Tämä osoittaa, että jos monet samankokoiset näytteet otetaan n, 68% heistä antaa keskiarvot alueella [ - ε, + ε].

On yksinkertainen sääntö, nimeltään Sääntö 68-95-99.7 Tämän avulla voimme löytää marginaalin näytevirhe E Luottamustasoa 68%, 95% ja 99,7% helposti, koska tämä marginaali on 1⋅ε, 2⋅ε ja 3⋅ε vastaavasti.

Luotettavuustasolle γ

Jos hän Luottamustaso γ Se ei ole mikään yllä olevasta, joten näytteenottovirhe on keskihajonta σ kerrottuna tekijällä Zy, joka saadaan seuraavalla menettelyllä:

1.- Ensin merkitsevyystaso α joka on laskettu Luottamustaso γ Seuraavan suhteen kautta: α = 1 - γ

Voi palvella sinua: Bayes -lause

2.- Sitten sinun on laskettava arvo 1 - α/2 = (1 + γ)/2, joka vastaa normaalia taajuutta, joka on kertynyt välillä -∞ ja Zy, Normaalissa tai Gaussin jakautumisessa tyypillinen F (z), jonka määritelmä voidaan nähdä kuvasta 2.

3.- Yhtälö on ratkaistu F (zy) = 1 - α/2 Normaalin jakautumistaulukoiden kautta (kertynyt) F, o F-1.

Jälkimmäisessä tapauksessa sinulla on:

Zy = g-1(1 - α/2).

4.- Lopuksi sovelletaan tätä kaavaa näytteenottovirheen kanssa luotettavuustasolla γ:

E = zy⋅(σ/√n)

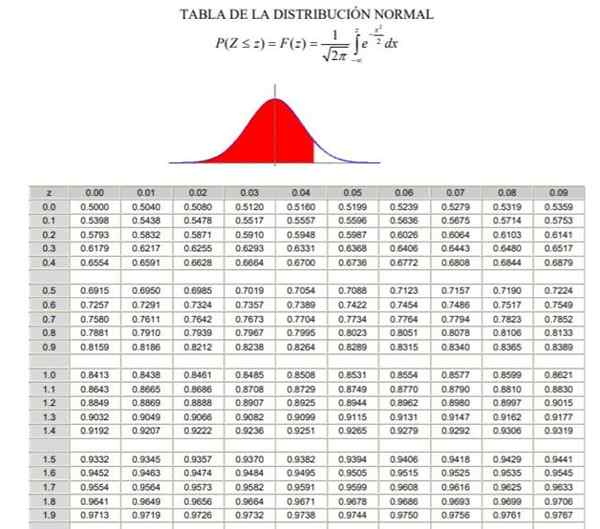Kuva 2. Normaali jakautumispöytä. Lähde: Wikimedia Commons.

Esimerkit

- Esimerkki 1

Laske Vakiovirhemarginaali 100 vastasyntyneen näytteen keskimääräisestä painosta. Keskimääräisen painon laskeminen oli = 3 100 kg keskihajonnan kanssa σ = 1 500 kg.

Ratkaisu

Hän Vakiovirhemarginaali On ε = σ/√n = (1 500 kg)/√100 = 0,15 kg. Mikä tarkoittaa, että näiden tietojen avulla voidaan päätellä, että 68%: n vastasyntyneiden paino on välillä 2950 kg - 3.25 kg.

- Esimerkki 2

Määrittää näytevirheen marginaali ja ja 100 vastasyntyneen painoalue, jolla on 95%: n luottamustaso, jos keskimääräinen paino on 3 100 kg keskihajonnan kanssa σ = 1 500 kg.

Ratkaisu

Jos Sääntö 68; 95; 99.7 → 1⋅ε; 2⋅ε; 3⋅ε, Sinulla on:

E = 2⋅ε = 2⋅0,15 kg = 0,30 kg

Toisin sanoen 95 prosentilla vastasyntyneistä on pesoja 2800 kg - 3 400 kg.

- Esimerkki 3

Määritä esimerkin 1 PESOS -alue 99,7%: n luottamusmarginaalilla.

Voi palvella sinua: Rhomboid: Ominaisuudet, kuinka kehä ja alue vie pois

Ratkaisu

Näytevirhe, jolla on 99,7% luottamusta 3 σ/√n, että esimerkillemme on E = 3 *0,15 kg = 0,45 kg. Täältä päätellään, että 99,7 prosentilla vastasyntyneistä on pesoja 2 650 kg - 3 550 kg.

- Esimerkki 4

Määritä tekijä Zy Luotettavuusastelle 75%. Määritä näytteenottovirhemarginaali tällä luotettavuustasolla esimerkissä 1 nostetulle tapaukselle.

Ratkaisu

Hän luottamustaso On γ = 75% = 0,75, joka liittyy merkitsevyystaso α Suhteen kautta γ= (1 - α), niin että merkitsevyystaso on α = 1 - 0,75 = 0,25.

Tämä tarkoittaa, että kertynyt normaali todennäköisyys -∞ ja Zy On:

P (z ≤ Zy ) = 1 - 0,125 = 0,875

Mikä vastaa arvoa Zy 1 1503, kuten kuvassa 3 esitetään.

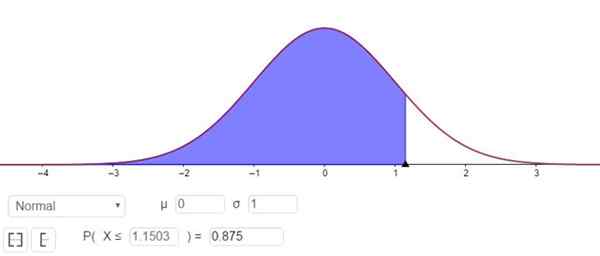Kuva 3. Zy -tekijän määrittäminen, joka vastaa 75%: n luottamustasoa. Lähde: f. Zapata Geogebran kautta.

Toisin sanoen näytteenottovirhe on E = zy⋅(σ/√n)= 1.15⋅(σ/√n).

Kun sitä sovelletaan esimerkki 1 tietoon, se antaa virheen:

E = 1,15*0,15 kg = 0,17 kg

75%: n luottamustasolla.

- Harjoitus 5

Mikä on luottamustaso, jos zα/2 = 2.4 ?

Ratkaisu

P (z ≤ zα/2 ) = 1 - α/2

P (z ≤ 2.4) = 1 - α/2 = 0,9918 → α/2 = 1 - 0,9918 = 0,0082 → α = 0,0164

Merkitysaste on:

α = 0,0164 = 1,64%

Ja lopuksi, luottamuksen taso on edelleen:

1- α = 1 - 0,0164 = 100% - 1,64% = 98,36%

Viitteet

  1. Canavos, G. 1988. Todennäköisyys ja tilastot: Sovellukset ja menetelmät. McGraw Hill.
  2. DeVore, J. 2012. Tekniikan ja tieteen todennäköisyys ja tilastot. Kahdeksas. Painos. Kyynärmä.
  3. Levin, r. 1988. Järjestelmänvalvojien tilastot. Toinen. Painos. Prentice Hall.
  4. Sudman, S.1982. Kysymykset: käytännön opas kyselylomakkeen suunnitteluun. San Francisco. Jossey basso.
  5. Walpole, r. 2007. Tekniikan ja tieteen todennäköisyys ja tilastot. Pearson.
  6. Wonnacott, t.H. ja r.J -. Wonnacott. 1990. Johdantotilastot. 5. ed. Viiva
  7. Wikipedia. Näytevirhe. Haettu: vuonna.Wikipedia.com
  8. Wikipedia. Virhemarginaali. Haettu: vuonna.Wikipedia.com