U -testi Mann - Whitney Mikä on ja sovelletaan, suorita, esimerkki

Se U -testi Mann - Whitney Sitä käytetään kahden riippumattoman näytteen vertailuun, kun heillä on vähän tietoa tai ne eivät noudata normaalia jakaumaa. Tällä tavoin sitä pidetään testinä ei parametrinen, Toisin kuin kollegasi Opiskelija -t -testi, Sitä käytetään, kun näyte on riittävän suuri ja seuraa normaalia jakautumista.

Frank Wilcoxon ehdottaa sitä ensimmäistä kertaa vuonna 1945 identtisten kokoisten näytteiden kohdalla, mutta kaksi vuotta myöhemmin sitä pidennettiin eri kokoisten näytteiden tapauksessa Henry Mann ja D. R -. Whitney.

Kuvio 1. Mann -testi - Whitney sovelletaan riippumattomien näytteiden vertailuun. Lähde: Pixabay.

Usein testiä käytetään tarkistamaan, onko laadullisen muuttujan ja toisen kvantitatiivisen välinen suhde.

Havainnollistava esimerkki on ottaa joukko hypertensiivisiä ihmisiä ja poimia kaksi ryhmää, joille päivittäinen verenpainetiedot kirjataan kuukaudeksi.

Yhdelle ryhmälle hoitoa a ja toinen sovelletaan hoitoa b. Tässä verenpaine on kvantitatiivinen muuttuja ja hoidon tyyppi on laadullinen.

Haluat tietää, onko mitattujen arvojen mediaani, ei keskiarvo, tilastollisesti yhtä suuri vai erilainen, sen selvittämiseksi, onko molempien käsittelyjen välillä ero. Vastauksen saamiseksi Wilcoxon tai U -testi Mann - Whitney sovelletaan.

[TOC]

Ongelmalähestymistapa Mannin testillä - Whitney

Toinen esimerkki, jossa testiä voidaan soveltaa, on seuraava:

Oletetaan, että haluat tietää, eroaako virvoitusjuomien kulutus merkittävästi kahdella alueella.

Yksi niistä on nimeltään Alue A ja toinen alue B. Kahden näytteen viikoittain kulutetut litrat viikoittain: yksi kymmenestä ihmisestä alueelle A ja toinen viidestä henkilöstä alueelle B.

Tiedot ovat seuraavat:

-Alue A: 16, 11, 14, 21, 18, 34, 22, 7, 12, 12

-Alue B: 12,14, 11, 30, 10

Seuraava kysymys nostetaan:

Onko virvoitusjuomien kulutus (y) riippuvainen alueesta (x)?

Laadulliset muuttujat verrattuna kvantitatiivisiin muuttujiin

-Laadullinen muuttuja x: Alue

-Kvantitatiivinen muuttuja ja: Kaasumainen kulutus

Jos kulutetun litran määrä on sama molemmilla alueilla, johtopäätös on, että kahden muuttujan välillä ei ole riippuvuutta. Tapa tietää on verrata kahden alueen keskimääräistä tai mediaanisuuntausta.

Normaali tapaus

Jos tiedot seurasivat normaalia jakaumaa, nostetaan kaksi hypoteesia: NULL H0 ja H1 -vaihtoehto vertailun avulla:

Voi palvella sinua: merkittäviä tuotteita

-H0: Kahden alueen keskiarvon välillä ei ole eroa.

-H1: Molempien alueiden keinot ovat erilaisia.

Tapaus ilman normaalia taipumusta

Päinvastoin, jos tiedot eivät noudata normaalia jakautumista tai yksinkertaisesti näyte on hyvin pieni, sen sijaan, että verrataan keskiarvoa, sitä verrataan Mediaani kahdesta alueesta.

-H0: Kahden alueen mediaanin välillä ei ole eroa.

-H1: Molempien alueiden mediaanit ovat erilaisia.

Jos mediaanit osuvat, niin nollahypoteesi täyttyy: soodan kulutuksen ja alueen välillä ei ole suhdetta.

Ja jos päinvastoin tapahtuu, vaihtoehtoinen hypoteesi on totta: kulutuksen ja alueen välillä on suhde.

Juuri näissä tapauksissa U -testi Mann - Whitney on ilmoitettu.

Näyte- tai ei -parirakennukset

Seuraava tärkeä kysymys päättää, sovelletaanko Mann Whitneyn U -testi.

Jos kaksi näytettä pariksi otetaan pariksi, alkuperäistä Wilcoxon -versiota sovellettaisiin. Mutta jos ei, kuten esimerkin tapaus, sovelletaan muokattua Wilcoxon -testiä, joka on tarkalleen Mann Whitney's -testi.

Mann Whitney U -testiominaisuudet

Mann -testi -Whitney ei -parametrinen testi, jota voidaan soveltaa näytteisiin, jotka eivät noudata normaalia jakaumaa tai muutaman tiedon kanssa. Sillä on seuraavat ominaisuudet:

1.- Vertaa mediaaneja

2.- Toimii tilatuilla alueilla

3.- Se on vähemmän voimakas, ymmärrettävä voimalla todennäköisyys hylätä nollahypoteesi, kun todellisuudessa se on väärä.

Kun nämä ominaisuudet otetaan huomioon, Mann -testi - Whitney sovelletaan:

-Tiedot ovat riippumattomia

-He eivät noudata normaalia jakaumaa

-NULL H0 -hypoteesi hyväksytään, jos kahden näytteen väliaine vastaa: MA = MB

-H1 -vaihtoehtoinen hypoteesi hyväksytään, jos kahden näytteen väliaine eroa: MA ≠ MB

Mann -kaava - Whitney

U -muuttuja on Mann - Whitney -testissä käytetty kontrastisivusto ja se on määritelty:

U = min (ua, ub)

Tämä tarkoittaa, että u on vähiten UA: n ja UB: n välillä, jota käytetään jokaiseen ryhmään. Esimerkissämme se olisi jokaiselle alueelle: a o b.

UA- ja UB -muuttujat määritetään ja lasketaan seuraavan kaavan mukaan:

Ua = nb + na (na +1)/2 - ra

Ub = nb + nb (nb +1)/2 - rb

Voi palvella sinua: samanlaisten termien vähentäminen

Tässä NA- ja NB -arvot ovat näytteiden koot, jotka vastaavat alueita A ja B, ja toisaalta RA ja RB ovat etäisyyssummat että määrittelemme alla.

Vaiheet testin soveltamiseksi

1.- Tilaa kahden näytteen arvot.

2.- Määritä tilausalue jokaiselle arvolle.

3.- Oikea olemassa olevat ligatuurit (toistuvat arvot).

4.- Laske näytteen a RA = summa a.

5.- Löydä RB = näytteen B alueiden summa.

6.- Määritä UA- ja UB -arvo edellisessä osassa annettujen kaavojen mukaan.

7.- Vertaa UA: ta ja UB: tä, ja kahdesta alaikäinen on osoitettu tai kokeellinen tilasto (ts. Tiedot) verrattuna teoreettiseen tai normaaliin tilastoon verrattuna.

Sovelluksen käytännön soveltaminen

Nyt soveltamme edellä mainittua sooda -ongelmaan aikaisemmin nostettua:

Alue A: 16, 11, 14, 21, 18, 34, 22, 7, 12, 12

Alue B: 12,14, 11, 30, 10

Riippuen siitä, että molempien näytteiden keskiarvot ovat tilastollisesti samoja tai erilaisia, jatkamme tai hylkäämme nollahypoteesin: muuttujan ja x: n välillä ei ole suhdetta, ts. Sodan kulutus ei riipu alueesta:

H0: MA = MB

H1: MA ≠ MB

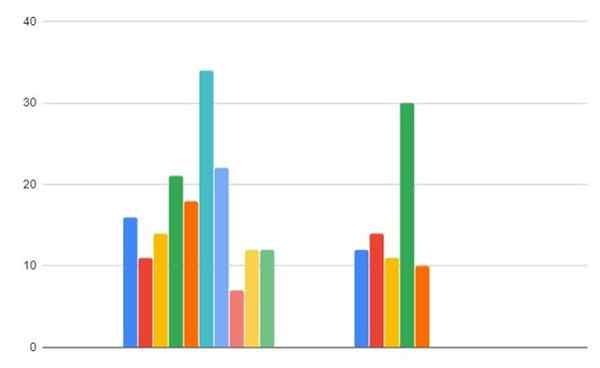Kuva 2. Kaasumainen kulutustiedot alueilla A ja B. Lähde: f. Zapata.

- Vaihe 1

Jatkamme tietojen tilaamista yhdessä kahdelle näytteelle tilaamalla arvot vähiten suurimmaksi:

Huomaa, että arvo 11 ilmestyy 2 kertaa (kerran jokaisessa näytteessä). Alun perin siinä on paikkoja tai alueita 3 ja 4, mutta ei yliarvioida tai aliarvioida yhtä tai toista. Keskimääräinen arvo valitaan alueeksi, eli 3,5.

Samoin 12 -arvoa jatketaan, joka toistetaan kolme kertaa alueilla 5, 6 ja 7.

No, arvolle 12 on määritetty keskimääräinen alue 6 = (5+6+7)/3. Ja sama arvolle 14, jolla on ligaatio (näkyy molemmissa näytteissä) asemissa 8 ja 9, keskimääräinen alue 8 määritetään.5 = (8+9)/2.

- Vaihe 2

Alueen A ja B tiedot erotetaan sitten uudelleen, mutta nyt niiden vastaavat alueet on osoitettu toisessa rivissä:

Alue A

Alue B

RB -alueet saadaan toisen rivin elementtien summista jokaiselle tapaukselle tai alueelle.

Vaihe 3

Vastaavat UA- ja UB -arvot lasketaan:

UA = 10 × 5 + 10 (10 + 1)/2 - 86 = 19

UB = 10 × 5 + 5 (5 + 1)/2 -34 = 31

Kokeellinen arvo u = min (19, 31) = 19

Vaihe 4

Teoreetian on tarkoitus seurata normaalia jakautumista n parametreilla, jotka annetaan yksinomaan näytteiden koon perusteella:

Voi palvella sinua: Irrationaaliset numerot: historia, ominaisuudet, luokittelu, esimerkit

N ((na⋅nb) /2, √ [nb (na + nb +1) /12]))

Muuttujan tai kokeellisesti saadun vertaamiseksi teoreettisen kanssa on tarpeen tehdä muuttuja muutos. Se siirtyy muuttujasta tai kokeellisesta arvoon tyypillinen, jota kutsutaan Z -z, Jotta voitaisiin verrata tyypillistä normaalia jakautumista.

Muuttujan muutos on seuraava:

Z = (u - na.NB / 2) / √ [NA. NB (Na + NB + 1) / 12] 

On huomattava, että muuttujan muutoksen kannalta käytettiin teoreettisen jakauman parametrejä U: lle. Sitten uusi Z -muuttuja, joka on hybridi teoreettisen ja kokeellisen tai normaalijakauman välillä tyypillinen N (0,1).

Vertailukriteerit

Jos z ≤ za ⇒ NULL H0 -hypoteesi hyväksytään

Kyllä z> za ⇒ NULL H0 -hypoteesi hylätään

Tyypilliset kriittiset arvot riippuvat vaadittavan luottamuksen tasosta, esimerkiksi luottamustasolla α = 0,95 = 95%, joka on tavallisimmin kriittinen arvo Za = 1,96.

Tässä esitetyt tiedot:

Z = (u - nb / 2) / √ [nb (na + nb + 1) / 12] = -0,73

Joka on alle kriittisen arvon 1,96.

Sitten lopullinen johtopäätös on, että nollahypoteesi hyväksytään:

Sodan kulutuksessa ei ole eroa alueiden a ja b välillä.

Online -laskimet Mannin u -testille - Whitney

Tilastollisissa laskelmissa on erityisiä ohjelmia, mukaan lukien SPSS ja Minitab, mutta nämä ohjelmat maksetaan ja niiden käyttö ei ole aina yksinkertaista. Tämä johtuu siitä, että ne antavat niin monia vaihtoehtoja, että sen käyttö on käytännössä varattu tilastojen asiantuntijoille.

Onneksi on olemassa useita erittäin tarkkoja, ilmaisia ​​ja yksinkertaisia ​​verkko -ohjelmia, jotka sallivat muun muassa U -Whitney U -testit.

Nämä ohjelmat ovat:

-Yhteiskuntatieteelliset tilastot (Socscistatistics.com), jolla on sekä U-Whitney U -testi että Wilcoxonin tasapainotettujen tai parillisten näytteiden tapauksessa.

-AI-terapiatilastot (Ai-terapia.com), jolla on useita tavanomaisia ​​kuvaavia tilastotestejä.

-Tilastollinen käyttö (fysiikka.CSBSju.EDU/STATS), yksi vanhimmista, joten käyttöliittymä voi näyttää vanhentuneelta, vaikka se on erittäin tehokas ilmainen ohjelma.

Viitteet

1. Dietrichson. Kvantitatiiviset menetelmät: Ranges -testi. Palautettu: Bookidown.org
2. Marín J P. SPSS -opas: Analyysi ja menettelyt ei -parametrisissa testeissä. Toipunut: Halweb.UC3M.On
3. USAL MOOC. Ei -parametrinen testi: U of Mann - Whitney. Palautettu: YouTube.com
4. Wikipedia. U -testi Mann - Whitney. Palautettu: on.Wikipedia.com
5. Xlstat. Avustuskeskus. Mann Test -opetusohjelma - Whitney in Excel. Toipunut: Ohje.XLSAT.com