Päätelmätilastot historia, ominaisuudet, mihin se on, esimerkkejä

Se Päätelmätilastot tai deduktiiviset tilastot ovat sellainen, joka päättelee siitä poistettujen näytteiden populaation ominaisuudet analyysitekniikoiden avulla. Saatujen tietojen avulla on kehitetty malleja, jotka sallivat sitten ennusteet mainitun väestön käyttäytymisestä.

Siksi päätelmätilastoista on tullut ykkönen tiede, joka tarjoaa ravintoa ja instrumentteja, joita lukemattomat tieteenalat vaativat päätöksenteossa.

Fysiikka, kemia, biologia, tekniikka ja yhteiskuntatieteet hyötyvät jatkuvasti näistä työkaluista, kun ne luovat mallinsa ja suunnittelevat ja toteuttavat kokeita.

[TOC]

Lyhyt historia päätelmätilastoista

Tilastot syntyivät muinaisina aikoina, koska ihmisten tarvetta organisoida asioita ja optimoida resursseja. Ennen kirjoittamisen keksintöä toteutettiin ihmisten lukumäärästä ja karjan lukumäärästä symbolien kautta, jotka oli tallennettu kiveen.

Myöhemmin kiinalaiset, babylonian ja egyptiläiset hallitsijat jättivät tietoja savitabletteihin, sarakkeisiin ja monumenteihin tallennettujen asukkaiden määrästä ja asukkaiden määrästä.

Rooman imperiumi

Kun Rooma käytti verkkotunnustaan ​​Välimerellä, viranomaisten oli yleistä suorittaa väestölaskenta viiden vuoden välein. Itse asiassa sana "tilastollinen" tulee italialaisesta sanasta tilasto, Mitä tarkoittaa ilmaista.

Samanaikaisesti Amerikassa suuret Kolumbian valtakunnat toivat myös samanlaisia ​​levyjä.

Keskiaika

Keskiajalla Euroopan hallitukset ja kirkko rekisteröivät maan omaisuuden. Sitten he tekivät saman syntymä-, kaste-, avioliitto- ja kuolemantapaukset.

Moderni ikä

Englanninkieliset tilastot John Graunt (1620-1674) teki ensimmäisenä ennusteita tällaisten luetteloiden perusteella, kuten kuinka monet ihmiset voivat kuolla tietyistä sairauksista ja naisten ja miesten syntymien arvioidusta osuudesta. Siksi demografian isää harkitaan.

Nykyaikainen

Myöhemmin, todennäköisyyden teorian myötä tilastot lakkasivat olevan pelkkä kokoelma organisaatiotekniikoita ja saavuttivat epäilyttään ennustavan tieteenä.

Siten asiantuntijat pystyivät.

Ominaisuudet

Alla on tämän tilastohaaran merkittävimmät ominaisuudet:

- Päätelmätilastot Tutki populaatio, joka ottaa siitä edustavan näytteen.

- Näytteen valinta suoritetaan erilaisilla toimenpiteillä, sopivin ovat ne, jotka valitsevat komponentit satunnaisesti. Siten millä tahansa populaation elementillä on sama todennäköisyys valita, ja sen kanssa vältetään ei -toivotut puolueellisuudet.

Voi palvella sinua: Kuinka muuntaa km/h a m/s? Ratkaisut

- Kerättyjen tietojen järjestämiseksi se käyttää kuvaavia tilastoja.

- Otoksesta lasketaan tilastolliset muuttujat, jotka arvioivat populaation ominaisuudet.

- Päätelmä- tai deduktiiviset tilastot hyödyntävät todennäköisyysteoriaa satunnaisten tapahtumien tutkimiseksi, ts. Jokaiselle tapahtumalle annetaan tietty esiintymisen todennäköisyys.

- Rakenna hypoteesit -supitions - populaation parametreista ja kontrast ne, tietää, ovatko ne oikein vai eivät myös laskeneet vastauksen luottamustason, ts. Se tarjoaa virhemarginaalin. Ensimmäistä menettelyä kutsutaan hypoteesitestit, Vaikka virhemarginaali on luottamusväli.

Mitkä ovat kuvaavia tilastoja? Sovellukset

Päätelmätilastot: välttämättömiä päätöksenteko- ja laadunvalvonnan tekemisessä

Tutki kokonaisuudessaan väestö voi vaatia paljon resursseja rahassa, ajassa ja vaivaa. On edullista ottaa edustavia näytteitä, jotka ovat paljon hallittavissa, keräävät tietoja niiden kautta ja luoda hypoteeseja tai oletuksia näytteen käyttäytymisestä.

Kun hypoteesit on vahvistettu ja niiden pätevyys on ristiriidassa, tulokset ulottuvat väestöön ja niitä käytetään päätöksentekoon.

Ne auttavat myös luomaan kyseisen väestön malleja, tekemään tulevia ennusteita. Siksi päätelmätilastot ovat erittäin hyödyllinen tiede:

Sosiologia ja väestötutkimukset

Nämä ovat ihanteellisia sovelluskenttiä, koska tilastollisia tekniikoita sovelletaan ajatukseen ihmisen käyttäytymisen erilaisten mallien luomisesta. Jotain, mikä etukäteen on melko monimutkainen, koska monet muuttujat puuttuvat asiaan.

Politiikassa käytetään paljon vaalien aikana äänestäjien äänestyksen taipumuksen tuntemiseen, tällä tavoin osapuolten suunnittelustrategiat.

Tekniikka

Päätelmätilastomenetelmiä käytetään laajasti tekniikassa, tärkeimmät sovellukset ovat laadunvalvonta ja prosessien optimointi, esimerkiksi tehtävien suorittamisen ajan parantaminen sekä työtapaturmien ehkäisy.

Talous ja liiketalous 

Deduktiivisilla menetelmillä voidaan suorittaa ennusteita yrityksen toiminnasta, odotettavissa olevasta myyntitasosta ja auttaa päätöksenteossa.

Esimerkiksi tekniikoitasi voidaan käyttää arvioimaan ostajien reaktio uuteen tuotteeseen, lähellä markkinoille lanseerausta.

Sen tarkoituksena on myös arvioida, mitkä ihmisten kulutustottumuksen muutokset ovat tärkeitä tapahtumia, kuten covid -epidemia.

Esimerkkejä päätelmätilastoista

Esimerkki 1

Yksinkertainen deduktiivinen tilastollinen ongelma on seuraava: Matematiikan opettaja vastaa viidestä ala -algebran osasta yliopistossa ja päättää käyttää niiden osioiden keskimääräisiä muistiinpanoja kaikkien keskiarvon arvioimiseksi.

Voi palvella sinua: Amorfisten lukujen likimääräinen mittaus: Esimerkki ja liikuntaKuitenkin suurta populaatiota voidaan tutkia edustavan näytteen kautta. Lähde: Pixabay.

Toinen mahdollisuus on ottaa näyte jokaisesta osasta, tutkia sen ominaisuuksia ja laajentaa tulokset kaikkiin osiin.

Esimerkki 2

Naisten vaatekaupan johtaja haluaa tietää, kuinka paljon tietty pusero myydään kesäkaudella. Tätä varten analysoidaan vaatteiden myynti kauden kahden ensimmäisen viikon aikana ja määritä siten trendi.

Peruskonseptit päätelmätilastoissa

On olemassa useita keskeisiä käsitteitä, mukaan lukien sellaiset, jotka tulevat todennäköisyyden teoriasta, joka on välttämätöntä, jotta voidaan ymmärtää näiden tekniikoiden kaiken laajuuden ymmärtäminen. Jotkut väestönä ja näytteinä olemme jo maininneet koko tekstin ajan.

Tapahtuma

Tapahtuma tai tapahtuma on jotain mitä tapahtuu, ja sillä voi olla useita tuloksia. Tapahtumaesimerkki voi olla valuutan käynnistäminen, ja tuloksia on kaksi mahdollista: kasvot tai sinetti.

Esimerkkitila

Se on joukko tapahtuman mahdollisia tuloksia.

Väestö ja otos

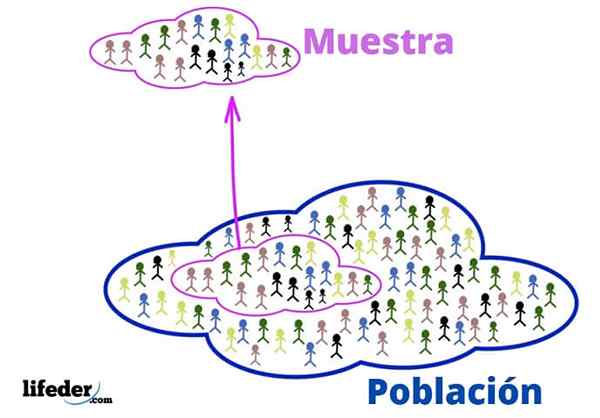Väestö ja otos

Väestö on maailmankaikkeus opiskelemaan. He eivät välttämättä koske eläviä ihmisiä tai olentoja, koska väestö, tilastoissa, voi koostua esineistä tai ideoista.

Omasta osastaan ​​otos on väestöjoukko, joka on poistettu siitä huolellisesti edustajasta.

Näytteenotto

Se on tekniikkajoukko, jonka kautta näyte valitaan tietystä populaatiosta. Näytteenotto voi olla satunnaista, jos näytettä käytetään todennäköisyysmenetelmiä tai todennäköisyyttä, jos analyytikolla on oma valintakriteeri, heidän kokemuksensa mukaan.

Tilastolliset muuttujat

Arvojoukko, jolla voi olla populaation ominaisuudet. Ne luokitellaan monin tavoin, esimerkiksi ne voivat olla hienovaraisia ​​tai jatkuvia. Lisäksi heidän luonteensa mukaan he voivat olla laadullisia tai kvantitatiivisia.

Todennäköisyysjakauma

Luonnossa havaittujen järjestelmien ja tilanteiden käyttäytymistä kuvaavat todennäköisyysfunktiot. Tunnetuimpia ovat Gaussin jakauma tai Gauss Bell ja Binomial jakauma.

Parametrit ja tilastot 

Arviointiteoriassa todetaan, että populaation arvojen ja kyseisen populaatiosta otetun otoksen välillä on yhteys. Se parametrit Ne ovat väestön ominaisuuksia, joita emme tiedä, mutta haluamme arvioida: esimerkiksi keskiarvo ja keskihajonta.

Puolestaan tilastollinen ovat näytteen ominaisuudet, esimerkiksi sen keskimääräinen ja keskihajonta.

Oletetaan esimerkiksi, että väestö koostuu kaikista 17–30 -vuotiaista yhteisöstä, ja halutaan tietää korkea -asteen koulutuksen nykyisten osuus. Tämä olisi määritettävä populaatioparametri.

Voi palvella sinua: lineaarinen interpolointi

Sen arvioimiseksi valitaan satunnainen otos 50 nuoresta ja heidän osuus yliopistossa tai korkea -asteen koulutuslaitoksessa lasketaan. Tämä osuus on tilastollinen.

Jos tutkimus suoritetaan, on määritetty, että 63 % 50: stä nuoresta tutkii korkeampaa, tämä on arvioitu populaatio, joka on tehty näytteestä.

Tämä on vain esimerkki siitä, mitä päätelmätilastot voivat tehdä. Sitä kutsutaan arviona, mutta tilastollisten muuttujien ennustamiseksi on myös tekniikoita sekä päätöksentekoa.

Tilastollinen hypoteesi

Se on oletus, joka tehdään keskiarvon arvosta ja väestölle jonkin ominaisuuden keskihajonta. Ellei väestöä tutkita kokonaan, nämä ovat tuntemattomia arvoja.

Hypoteesitestit

Ovatko väestöparametreihin tehdyt oletukset voimassa olevia oletuksia? Tietääksesi sen, tukevatko näytteen tulokset niitä vai eivät, joten on välttämätöntä suunnitella hypoteesitestit.

Nämä ovat yleisiä vaiheita sellaisen suorittamiseksi:

Vaihe 1

Tunnista jakautumistyyppi, jota populaation odotetaan seuraavan.

Vaihe 2

Nosta kaksi hypoteesia, merkittynä h_jompikumpi ja h₁. Ensimmäinen on nollahypoteesi jossa oletetaan, että parametrilla on tietty arvo. Toinen on Vaihtoehtoinen hypoteesi mikä on erilainen arvo kuin nollahypoteesi. Jos tämä hylätään, vaihtoehtoinen hypoteesi hyväksytään.

Vaihe 3

Luo hyväksyttävä marginaali parametrin ja tilastojen väliselle erolle. Ne ovat harvoin identtisiä, vaikka heidän odotetaan olevan hyvin lähellä.

Vaihe 4

Ehdottaa kriteeriä nollahypoteesin hyväksymiseksi tai hylkäämiseksi. Tätä varten käytetään testitilastoja, jotka voivat olla keskiarvo. Jos keskiarvo on tietyissä rajoissa, nollahypoteesi hyväksytään, muuten se hylätään.

Vaihe 5

Viimeisenä askeleena päätetään, hyväksytäänkö nollahypoteesi.

Kiinnostavia teemoja

Tilasto.

Tilastolliset muuttujat.

Väestö ja otos.

Kuvailevia tilastoja.

Viitteet

1. Berenson, m. 1985.Tilastot hallinnosta ja taloudesta, käsitteistä ja sovelluksista. Amerikanvälinen toimitus.
2. Canavos, G. 1988. Todennäköisyys ja tilastot: Sovellukset ja menetelmät. McGraw Hill.
3. DeVore, J. 2012. Tekniikan ja tieteen todennäköisyys ja tilastot. Kahdeksas. Painos. Cengage -oppiminen.
4. Tilastohistoria. Toipunut: Eumed.netto.
5. Ibañez, s. 2010. Matematiikka II. Pätevyyslähestymistapa. Cengage -oppiminen.
6. Levin, r. 1981. Järjestelmänvalvojien tilastot. Prentice Hall.
7. Walpole, r. 2007. Tekniikan ja tieteen todennäköisyys ja tilastot. Pearson.