Normaali ponnistus, mistä se koostuu, miten se lasketaan, esimerkkejä

Hän normaali ponnistus Tiettyyn materiaaliin, jota kutsutaan myös yksiaksiaaliseksi ponnisteluksi, se on kohtisuoran kohtisuoran sovelletun voiman välinen suhde tiettyyn pintaan ja ristikkäinen alue, jolla se toimii, tai kuorma pinta -alayksikköä kohti. Matemaattisesti, jos P on voiman suuruus ja A on alue, jolla sitä käytetään, ponnistus σ on osamäärä: σ = p/a.

Kansainvälisen järjestelmän normaalin ponnistelun yksiköt ovat Newton /Metro², tunnetaan nimellä Pascal ja lyhennetty PA. Nämä ovat samoja paineyksiköitä. Muut kirjallisuudessa esiintyvät yksiköt ovat usein puntia / tuumaa² jompikumpi psi.

Kuvio 1. Kivet altistetaan jatkuvasti tektonisen toiminnan takia, aiheuttaen muodonmuutoksia maankuoressa. Lähde: Pixabay.

Kuviossa 2 kahta yhtä suurta voimaa kohdistetaan kohtisuorassa ristikkäisen alueen suhteen, mikä tekee pitoa erittäin kevyestä palkista, jolla on taipumus laajentaa sitä.

Nämä voimat tuottavat normaalia vaivaa, jota kutsutaan myös Aksiaalikuorma keskitetty, koska sen toimintalinja osuu samanaikaisesti aksiaalitakselilla, jolle keskikohta sijaitsee.

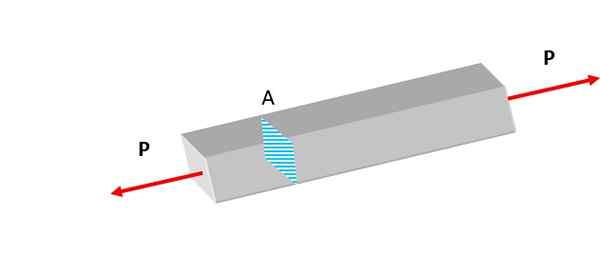Kuva 2. Esitetty palkki on vetovoimien alainen. Lähde: Itse tehty.

Pyrkimykset, olivatpa ne normaaleja tai muita tyyppejä, näyttävät jatkuvasti luonnossa. Litosfäärissä kivet ovat painovoiman ja tektonisen aktiivisuuden alaisia, kokeilevat muodonmuutoksia.

Tällä tavoin rakenteet, kuten taitokset ja viat.

[TOC]

Kuinka se lasketaan?

Alussa annettu yhtälö σ = P/A sallii laskemisen kyseisen alueen keskimääräisen normaalin ponnistelun laskemisen. P: n arvo on tuloksena olevan voiman voimakkuus keskikohtaan käytetyn alueen yli ja riittää moniin yksinkertaisiin tilanteisiin.

Tässä tapauksessa voimien jakautuminen on tasaista, etenkin pisteiden päässä siitä, missä sinulla on palkki veto- tai puristuksella. Mutta jos tietyssä vaiheessa on tarpeen ponnistelu tai voimat eivät ole jakautuneet tasaisesti, on tarpeen käyttää seuraavaa määritelmää:

Voi palvella sinua: suljettu sähköpiiri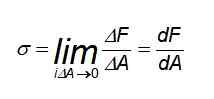

Sitten yleensä tietyssä pisteessä olevien ponnistelujen arvo voi olla erilainen kuin keskiarvo. Itse asiassa pyrkimys voi vaihdella harkittavana olevan jakson mukaan.

Tätä havainnollistetaan seuraavassa kuviossa, jossa vetovoimat f yrittää erottaa viiva tasapainosta osioissa mm ja nn.

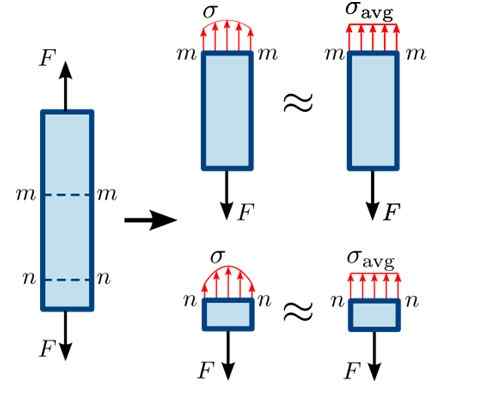Kuva 3. Normaalien ponnistelujen jakautuminen palkin eri osissa. Lähde: https: // commons.Wikimedia.org/wiki/tiedosto: normaali_stress.SVG#/Media/Tiedosto: Normal_stress.SVG

Kuten osio nn Se on hyvin lähellä sitä, missä voima f alas, voimien jakautuminen pinnalle ei ole täysin homogeeninen, nämä alaikäiset ovat sitä kauempana siitä lähtien. Jakelu on hiukan homogeenisempi osastossa mm.

Joka tapauksessa normaali pyrkimys pyrkii aina venyttämään tai puristamaan kehon kaksi osaa, jotka löytyvät sen tason molemmilta puolilta, joihin ne toimivat. Toisaalta muut erilaiset ponnistelut, kuten leikkaus, pyrkivät liikkumaan ja erottamaan nämä osat.

Hooken laki ja normaali työ

Hooken laissa todetaan, että joustavien rajojen sisällä normaali työ on suoraan verrannollinen palkin tai esineen kokemaan muodonmuutokseen. Siinä tapauksessa:

Normaali ponnistus ∝ yhtenäisen muodonmuutoksen

Suhteellisuusvakio on nuori (y) moduuli:

Normaali ponnistus (σ) = nuori moduuli (y) x yhtenäinen muodonmuutos (ε)

σ = y. ε

Ε = ΔL/L: n kanssa, missä ΔL on ero lopullisen ja alkuperäisen pituuden välillä, joka on L.

Nuori moduuli tai joustavuusmoduuli on ominaisuus materiaalille, jonka mitat ovat samat kuin ponnisteluissa, koska yksikön muodonmuutos on mitoiton.

Se voi palvella sinua: 13 esimerkkiä Newtonin toisesta laista jokapäiväisessä elämässä

Ponnistelujen merkitys materiaalien ja geologian vastustuskykyyn

Materiaalien kestävien ponnistelujen määrittäminen on erittäin tärkeää. Rakennusten rakentamisessa käytettyihin rakenteisiin sekä eri laitteiden osien suunnitteluun on tarpeen varmistaa, että valitut materiaalit täyttävät toiminnot oikein.

Siksi materiaaleja analysoidaan tyhjentävästi laboratorioissa tutkimusten kautta, joiden tarkoituksena on tietää, kuinka paljon voimaa he voivat vastustaa ennen muodonmuutoksia ja murtumista, menettäen siten toiminnonsa. Tämän perusteella tehdään päätös siitä, onko tietyn kappaleen valmistus vai ei osa laitetta.

Uskotaan, että ensimmäinen tutkija, joka tutkii systemaattisesti materiaalien vastustuskykyä, oli Leonardo da Vinci. Hän jätti todisteita kokeista, joissa hän määritteli erilaisten peson ripustettujen johtojen vastustuskykyä.

Pyrkimyksissä sekä voiman suuruus että rakenteen mittojen suuruus että sen sovellettiin on tärkeää, jotta voidaan määrittää rajat, joiden sisällä materiaalilla on joustava käyttäytyminen; eli se palaa alkuperäiseen muotoonsa, kun ponnistus lakkaa.

Näiden testien tuloksilla suoritetaan ponnistelujen muodostumiskäyrät erityyppisille materiaaleille, kuten teräs, betoni, alumiini ja monet muut.

Esimerkit

Seuraavissa esimerkeissä oletetaan, että voimat jakautuvat tasaisesti ja että materiaali on homogeeninen ja isotrooppinen. Tämä tarkoittaa, että sen ominaisuudet ovat samat mihin tahansa suuntaan. Siksi on pätevää käyttää yhtälöä σ = p/A ponnistelujen löytämiseksi.

-Harjoitus 1

Kuviossa 3 tiedetään, että AB -osioon liittyvällä keskimääräisellä normaalilla ponnistelulla on suuruusluokka 48 kPa. Löydä: a) CB: ssä toimiva voiman F suuruus, b) BC: n ponnistelu.

Se voi palvella sinua: Vaaka -ammunta: Ominaisuudet, kaavat ja yhtälöt, harjoitukset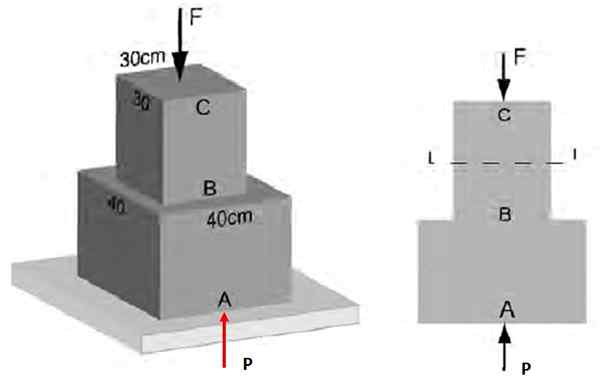Kuva 4. Normaalit ponnistelut esimerkin 1 rakenteeseen ..

Ratkaisu

Koska rakenne on staattisessa tasapainossa, Newtonin toisen lain mukaan:

P-f = 0

AB -osion normaalilla ponnisteluilla on suuruus:

σ_Ab = P/a_Ab

Missä p = σ_Ab . -Lla_Ab = 48000 PA. (40 x 10 ^-2 m)² = 7680 N

Siksi f = 7680 n

Normaali ponnistus osiossa BC on F: n ja poikkileikkauksen pinta -alan välinen suhde tällä puolella:

σ_BC = F/a_BC = 7680 N / (30 x 10 ^-2 m)² = 85.3 kPa.

-Harjoitus 2

150 m lanka pitkä ja 2.5 mm: n halkaisija venytetään 500 N: n voimalla. Löytö:

a) Pitkittäinen ponnistus σ.

b) Yhtenäiset muodonmuutokset tietäen, että lopullinen pituus on 150.125 m.

c) joustavuusmoduuli JA tämän langan.

Ratkaisu

a) σ = f / a = f / π.r -²

Langan säde on puolet halkaisijasta:

R = 1.25 mm = 1.25 x 10^-3 m.

Risti -aukko on π.r -², Sitten ponnistelu on:

σ = f / π.r -² = 500 / (π.(1.25 x 10^-3-A² PA = 101859.2 Pa

b) ε = ΔL / l = (lopullinen pituus - alkupituus) / alkupituus

Siksi:

ε = (150.125 - 150) /150 = 0.125/150 = 0.000833

c) Langan nuoren moduuli tyhjennetään tietämällä ε ja σ arvot aikaisemmin:

Y = σ / ε = 101859.2 Pa / 0.000833 = 1.22 x 10⁸ PA = 122 MPa.

Viitteet

1. Olut, f. 2010. Materiaalimekaniikka. Viides. Painos. McGraw Hill. 7 - 9.
2. Giancoli, D.  2006. Fysiikka: sovellusten periaatteet. 6^tth  Ed. Prentice Hall. 238-242.
3. Hibbeler, R.C. 2006. Materiaalimekaniikka. Kuudes. Painos. Pearson -koulutus. 22 -25
4. Valera Negrete, J. 2005. Yleiset fysiikan muistiinpanot. Yksinäinen. 87-98.
5. Wikipedia. Stressi (mekaniikka). Toipunut: Wikipedia.org.