Fyysinen

Kupera peili

Kupera peili

Mikä on kupera peili?

Hän kupera peili Tai erilainen on kaareva peili, melkein aina pallomaisesti ja heijastavan pinnan ollessa pallon ulkopuolella, kuten joulukuusen koristeet. Conpex -peilien ansiosta se on mahdollista.

Esimerkiksi kaduille sijoitetut peilit kapeiden ristien ajoneuvojen kauttakulun helpottamiseksi ovat kuperoja, koska ne tuottavat kuvan, jolla on laaja visuaalinen kenttä.

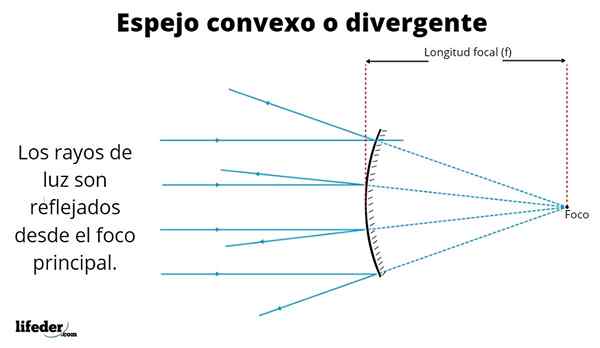
Kuva kupera peilistä

Näin muodostuneet kuvat ovat monipuolisia, riippuen paikasta, johon esine sijoitetaan. Ylivoimainen kuva näyttää rinnakkaiset säteet kaukaisesta suihkulähteestä, kuten aurinko.

Säteet heijastuvat heijastuslain mukaan, mikä osoittaa, että salaman esiintymiskulma on sama, jolla se heijastuu. Kuten voimme nähdä, heijastetut säteet erotetaan - ne eivät ylitä - kun ne poistuvat spekulaarisesta pinnasta, minkä vuoksi tällainen peili tunnetaan myös nimellä erilainen.

Kun heijastukset ulottuvat takaisin peilistä - epäjatkuvia viivoja kuviossa - nämä leikkaavat pisteeseen, jota kutsutaan Focusiksi.

Kuperan peilien ominaisuudet

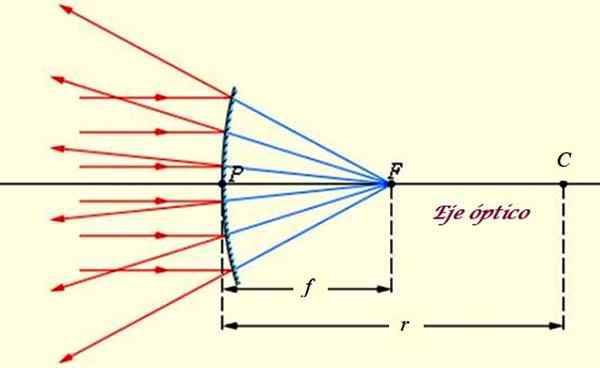Kupera tai erilainen peili, jolla etäisen suihkulähteen säteet, kuten aurinko vaikuttaa. Lähde: f. Zapata.

Conpex -peilillä on seuraavat ominaisuudet (katso erinomainen kuva):

-Peilin merkittävät kohdat ovat:

  • C Keskusta, joka vastaa sen pallon keskusta, johon peili kuuluu.
  • F Focus, jossa heijastuvat säteet heijastuvat peilin lähentymiseen.
  • Saman kärjen P, joka vastaa pallomaisen pinnan keskustaa ja on collineal C: n ja F: n kanssa.
Voi palvella sinua: ío (satelliitti)

-Haastaa optinen akseli jompikumpi pääakseli, mikä on linja kohtisuorassa spekulaariseen pintaan nähden. Optiseen akseliin vaikuttavat säteet heijastuvat samaan suuntaan.

-Pallon keskipiste, johon peili kuuluu, on pisteessä C ja R on sen säde. A C tunnetaan nimellä Kaarevuuskeskus, sillä aikaa r - onko hän Kaarevuussäde ja osoittaa kuinka kaareva peili on: alaikäinen r -, Korostavampi on kupera muoto.

-Heijastettujen säteiden leikkauspiste tunnetaan nimellä Keskipiste peilistä. F: n ja P: n välinen etäisyys on suunnilleen r -/2:

F = r/2

Tämä lauseke pätee peileihin, joiden koko on paljon pienempi kuin sen kaarevuussäde.

-Muodostuskuva on pienempi ja myös virtuaalinen, koska se sijaitsee peilin takana, kuten näemme seuraavaksi.

Kuvanmuodostus kuperassa peilissä

Tietäminen, kuinka kuperaan peiliin muodostuva kuva on säteenkäsittely, joka koostuu esineestä tulevien valonsäteiden edustamisesta suorien linjojen kautta.

Nämä säteet heijastuvat peilin pinnalle ja myös heijastuneet säteet vedetään. Ray -menetelmää voidaan soveltaa minkäänlaiseen peiliin, ei vain kuperiin.

Pidentämällä heijastuneita säteitä, ne leikkaavat tietyssä vaiheessa, ja juuri siinä kuva muodostuu. Laajennetusta esineestä puuna tulevien heijastuneiden säteiden pidennys esitetään alemmassa kuvassa epäjatkuvalla viivalla.

Objektin alemmassa kuviossa kolme sätettä vedetään, hyvin erityinen ja helppo piirtää, samoin kuin sen heijastukset:

Voi palvella sinua: Lämpölaajennus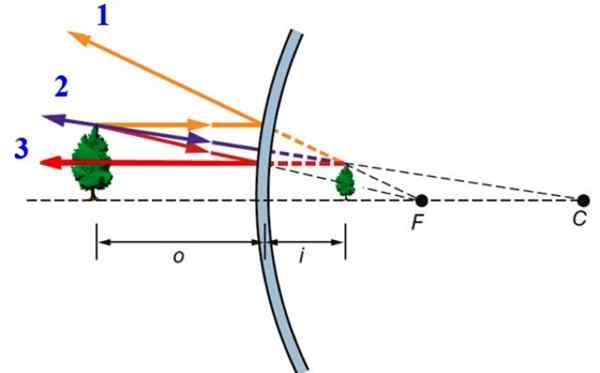 Kuva 2.- Kuvanmuodostus kuperassa peilissä. Lähde: f. Zapata.

-Ray 1, joka vaikuttaa yhdensuuntaisen optisen akselin kanssa.

-Ray 2, joka vaikuttaa heijastuneen säteen eksolointiin, kulkee tarkasti peilin keskittymisen kautta, ts. Piste F. Tämä säde heijastuu samanaikaisesti optisen akselin kanssa.

-Lopuksi Ray 3, joka ulottuu kohtisuoraan pallomaiseen pintaan, ja tästä syystä se heijastuu samaan suuntaan.

Periaatteessa tämä menettely koskee jokaista puun pistettä, mutta 3 piirrettyjen säteiden saatujen tietojen avulla se on riittävä löytää esineen kuvan: se muodostuu peilin takana, se on oikea ja pienempi kuin alkuperäinen.

Esimerkkejä ja sovelluksia kuperien peilien

Monet erittäin vedetyt pallomaiset pinnat toimivat kuperina peileinä, esimerkiksi kirkkaita ja hopeaa joulukoristeita, samoin kuin uusia ja kirkkaita teräslusikoita.

Myös kuperapeileillä on esimerkiksi monia käytännön sovelluksia:

Peilit liikenneonnettomuuksien estämiseksi

Kaduilla ja keinoilla olevat kuperat peilit auttavat välttämään onnettomuuksia, koska niiden avulla voit nähdä kulmista tulevan liikenteen.

Valvontapeilit

Kaupoissa ja pankeissa on yleensä kuperia peilejä varkaiden havaitsemiseksi sekä ihmisten ja haarukkaiden välisten törmäyksien välttämiseksi, jotka kiertävät salissa ja hyllyjen välillä.

Taustapeilit

Autoissa ja moottoripyörissä on kuperat peilit, jotka tuottavat hieman pienempiä kuvia, mutta peittävät enemmän visuaalista kenttää kuin litteät peilit.

Cassegrain -teleskooppi

Yksi cassegrain -heijastimen peileistä, toissijainen peili, on kupera, vaikka se ei ole pallomainen ja heijastaa kuvaa kohti kaukoputken pääpeiliä kohti.

Voi palvella sinua: Gravitaatioenergia: kaavat, ominaisuudet, sovellukset, harjoitukset

Kupera peiliyhtälöt

Harkitse seuraavan kuvan suorakulmioita, jotka määritetään säteellä 1, joka tulee nuolen yläosasta, sen heijastus ja tämän jatkaminen.

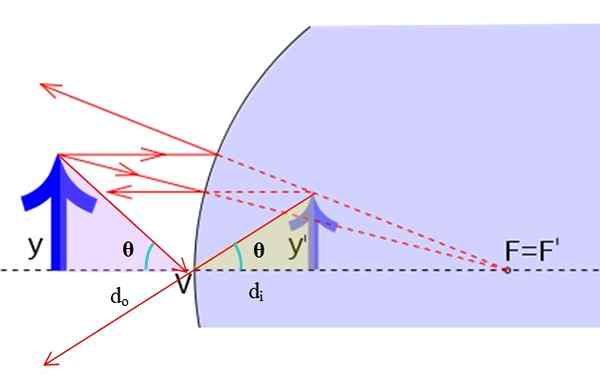Geometria peilin suurennuksen löytämiseksi. Lähde: f. Zapata.

Alkuperäisellä kuvalla on korkeus ja vaikka virtuaalisen kuvan korkeus on ja ' . Onko totta että:

Tan θ = y/djompikumpi = Y '/dYllyttää

Peilin suurennus

Syynä kuvan korkeuden ja esineen korkeuden välillä on peilin suurennus, Sitä kutsutaan, vaikka saatu kuva on pienempi kuin todellinen objekti. Merkitsemme sitä m-

M = y '/ y = dYllyttää /Djompikumpi

Objektin ja sen kuvan välinen suhde kuperassa peilissä

Tarkastellaan nyt tätä toista lukua, jossa AVF -aluetta voidaan pitää suunnilleen oikeana kolmiona, koska peilin kaarevuus ei ole kovin voimakas. Siksi:

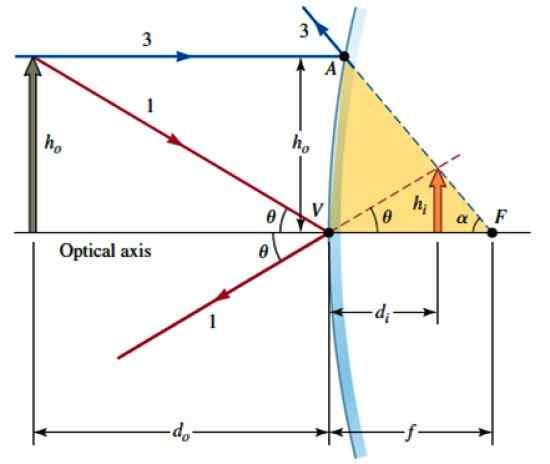Geometria löytääkseen matemaattisen suhteen objektin ja sen kuvan välillä. Lähde: Katz, D. Fysiikka tutkijoille ja insinööreille.

Av ≈ Hjompikumpi

Niin:

Tan α = h

Siksi:

Tämän lausekkeen käänteinen on suurennus, sitten:

Siksi:

1- (DYllyttää /f) = DYllyttää /Djompikumpi

Jakamalla kaikki D: n välilläYllyttää-

Lopuksi:

 Nyt peileille on joitain merkkejä koskevia sopimuksia. Itse asiassa, vaikka tiedämme, että etäisyys on aina positiivinen, kaikilla peilin takana olevilla etäisyyksillä, ne erotetaan negatiivisella merkinnällä.

Siksi F ja d -dYllyttää He ovat peilin takana, ne laitetaan merkki vähemmän, kun taas etäisyydelle Djompikumpi Se ei ole välttämätöntä, koska se on peilin edellä. Siten edellinen yhtälö säilyy:

Voidaan osoittaa, että tämä yhtälö pätee myös koveralle peilille.

Viitteet

  1. Bauer, W. 2011. Fysiikka tekniikkaan ja tieteisiin. Nide 2. MC Graw Hill.
  2. Giambattista, a. 2010. Fysiikka. Toinen. Ed. McGraw Hill.
  3. Katz, D. 2017. Fysiikka tutkijoille ja insinööreille. Cengage -oppiminen.
  4. Thomas, W. 2008. Käsitteellinen fysiikka. McGraw Hill.
  5. Tippens, P. 2011. Fysiikka: Käsitteet ja sovellukset. 7. painos. McGraw Hill.