Kuvaileva tilastohistoria, ominaisuudet, esimerkit, käsitteet

Se Kuvailevia tilastoja Tilastojen haara käsittelee tiedon keräämistä ja järjestämistä monien elementtien järjestelmien käyttäytymisestä, joka tunnetaan yleisesti nimellä nimellä väestö.

Tätä varten se käyttää numeerisia ja graafisia tekniikoita, joiden kautta se tarjoaa tietoa tekemättä ennusteita tai päätelmiä väestöstä, missä se tulee.

Kuvailevia tilastoja katsotaan järjestämään ja esittämään tietoa kätevästi

[TOC]

Historia

Vanhuus

Tilastot ovat peräisin ihmisen tarpeesta organisoida tarvittavat tiedot sen selviytymiseen ja hyvinvointiin sekä siihen vaikuttavia tapahtumia varten. Antiikin suuret sivilisaatiot jättivät uudelleensijoittajien, kerättyjen verojen, sadon määrän ja armeijoiden koon tietueet.

Esimerkiksi hänen pitkän hallituskautensa aikana Ramses II (1279-1213.C) Tilasi Egyptin väestölaskennan ja asukkaat, joilla oli siihen mennessä noin 2 miljoonaa asukasta.

Samoin Raamattu, joka Moses suoritti väestölaskennan tietääkseen kuinka monella sotilaalla oli kaksitoista Israelin heimoa.

Myös muinaisissa Kreikassa ihmiset ja resurssit tehtiin. Roomalaiset, jotka ovat merkittäviä korkeasta organisaatiostaan, rekisteröivät väestön määräajoin valmistelemalla väestölaskentaa joka viides vuosi, mukaan lukien alueet ja resurssit.

renessanssi

Rooman vähentymisen jälkeen tärkeät tilastotiedot pelkäsivät renessanssin saapumiseen saakka, kun tilastot pintavat.

Seitsemännentoista vuosisadan huipentuma, todennäköisyysteoria syntyi, mikä johtuu ihmisten taipumuksesta uhkapeleihin, mikä tarjosi tilastotiedot matemaattisen kurinalaisuuden, joka teki siitä itsessään tieteen.

Moderni ikä

Uusi impulssi tuli virheiden teoriaan ja vähimmäisryhmät 1800 -luvulla, jotka noudattivat muuttujien välistä korrelaatiomenetelmää, arvioidakseen niiden välistä suhdetta kvantitatiivisesti.

Lopuksi saakka, 2000 -luvulla, tilastot ulottuivat jokaiseen tieteen ja tekniikan haaraan välttämättömänä työkaluna ongelmanratkaisussa.

Kuvailevien tilastojen ominaisuudet

Kuvaileville tilastoille on ominaista:

- Järjestä tiedon ja grafiikan kerätyt tiedot. Kaaviot voivat olla monipuolisia: histogrammit, taajuuden monikulmiot, kakkujen muotoiset kaaviot, muun muassa.

- Levitä tietoja taajuusalueilla heidän hallinnan helpottamiseksi. Käytä aritmeettista löytääksesi datan edustavimmat arvot keskeisten taipumusmittausten avulla ja analysoimaan niiden leviämistä.

- Määritä jakaumien muoto, niiden symmetria, jos ne ovat keskitettyjä tai puolueellisia, ja jos ne ovat teräviä tai melko litistettyjä.

Voi palvella sinua: implisiittiset johdannaiset: miten ne on ratkaistu ja ratkaistuihin harjoituksiin

Mitkä ovat kuvaavia tilastoja?

Aina kun se on välttämätöntä.

Sitten mainitsemme joitain esimerkkejä:

Talous

Kuvailevat tilastot käsittelevät tiedon rekisteröintiä ja järjestämistä väestöstä ja niiden ikä-, tuloista, sijoituksista, voittoista ja kuluista. Tällä tavoin hallitukset ja instituutiot suunnittelevat parannuksia ja sijoittavat asianmukaisesti.

Aputessasi seurata ostoksia, myyntiä, palautuksia ja palveluiden tehokkuutta. Tästä syystä tilastot ovat välttämättömiä päätöksenteossa.

Fysiikka ja mekaaninen

Fysiikka ja mekaniikka käyttävät tilastoja jatkuvan väliaineen tutkimiseen, jotka koostuvat suuresta määrästä hiukkasia, kuten atomeja ja molekyylejä. Osoittautuu, että kutakin niistä ei ole mahdollista seurata erikseen.

Mutta järjestelmän globaalin käyttäytymisen tutkiminen (esimerkiksi kaasuosa) makroskooppisesta näkökulmasta on mahdollista selvittää keskiarvot ja määritellä makroskooppiset muuttujat sen ominaisuuksien tuntemiseksi. Esimerkki tästä on kaasujen kineettinen teoria.

Lääke

Se on välttämätön työkalu tarkkailemalla sairauksia, sen alkuperästä ja sen kehityksen aikana sekä hoidon tehokkuutta.

Tilastot, jotka kuvaavat sairastuvuuden, paranemisen, inkubaatioaikojen tai sairauden kehitystä, ikä, jolla se yleensä näyttää ja tyylitiedot, ovat välttämättömiä tehokkaimpia hoitoja suunnitellessasi.

Ravitsemus

Yksi monista kuvailevien tilastojen sovelluksista on rekisteröidä ja tilata tietoja elintarvikkeiden kulutuksesta eri väestöryhmissä: niiden määrä, laatu ja eniten kulutettuja, monien muiden havaintojen joukossa, jotka kiinnostavat asiantuntijoita.

Esimerkkejä kuvaavista tilastoista

Alla näemme joitain esimerkkejä, jotka kuvaavat, kuinka hyödyllisiä kuvaavien tilastojen työkaluja auttavat tekemään päätöksiä:

Esimerkki 1

Koulujen ruokasalien parantamiseksi vaaditaan käyttäjätietoja. Lähde: Wikimedia Commons.

Maaseudun koulutusviranomaiset institutionaaliset parannukset. Oletetaan, että he toteuttavat uuden koulun ruokasalin järjestelmän.

Tätä varten on välttämätöntä olla tietoja opiskelijaväestöstä, esimerkiksi opiskelijoiden lukumäärä luokkaa kohti, ikä, sukupuoli, korkeus, paino- ja sosioekonominen tila. Sitten nämä tiedot esitetään taulukoiden ja kaavioiden muodossa.

Esimerkki 2

Seuratakseen paikallista jalkapallojoukkuetta ja tehdä uusia allekirjoituksia, johtajat kantavat pelattujen otteluiden lukumäärän, voittaneet, sidotut ja menettäneet, samoin kuin maalien, maalintekijöiden määrän ja kuinka he onnistuivat pisteyttämään: vapaapotku, puoli tuomioistuimesta, rangaistukset, rangaistukset, vasemman jalan tai oikean kanssa, muun muassa.

Se voi palvella sinua: toisiaan poissulkevat tapahtumat: ominaisuudet ja esimerkit

Esimerkki 3

Jäätelökaupassa on useita jäätelömakuja ja haluaa parantaa myyntiään, joten omistajat suorittavat tutkimuksen, jossa he laskevat asiakkaiden määrän, erottavat ne ryhmiin sukupuolen ja ikäryhmän mukaan.

Tässä tutkimuksessa kirjataan suosikki jäätelön maku ja myydyin esitys, esimerkiksi. Ja kerättyjen tietojen avulla he suunnittelevat makujen ja tarvittavat astioiden ja lisävarusteiden ostot valmistelua varten.

Kuvailevien tilastojen peruskäsitteet

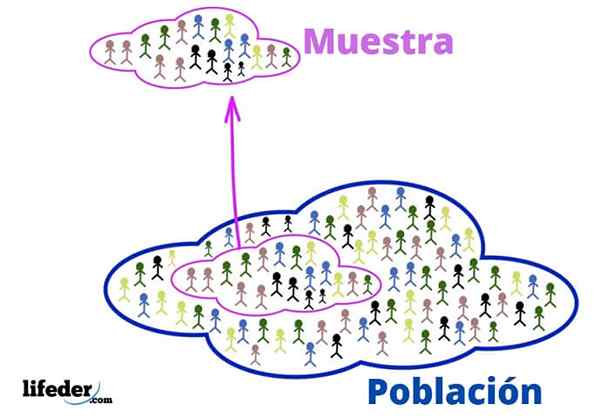Väestö ja otos

Nämä peruskäsitteet ovat välttämättömiä tilastollisten tekniikoiden soveltamiseksi, katsotaan:

Väestö

Tilastollisessa tilanteessa väestö viittaa maailmankaikkeuteen tai kollektiiviseen, josta tiedot tulevat.

Kyse ei aina ole ihmisistä, koska ne voivat olla sarjoja eläimiä, kasveja tai esineitä, kuten autoja, atomeja, molekyylejä ja jopa tapahtumia ja ideoita.

Näyte

Kun väestö on erittäin suuri, siitä poistetaan edustava näyte ja analysoidaan menettämättä asiaankuuluvaa tietoa.

Se voidaan valita satunnaisesti tai joidenkin analyytikon aiemmin asettamien kriteerien mukaan. Etuna on, että väestön osajoukko on paljon hallittavissa.

Muuttuva

Se viittaa arvojoukkoihin, jotka voivat ottaa tietyn väestölle. Tutkimus voi sisältää erilaisia ​​muuttujia, kuten ikä, sukupuoli, paino, akateeminen taso, siviiliasema, tulot, lämpötila, väri, aika ja monet muut.

Muuttujat voivat olla luonteeltaan erilaisia, joten niiden luokittelemiseksi on kriteerejä ja antaa heille sopivin hoito.

Kategoriset muuttujat ja numeeriset muuttujat

Niiden mittaamisen mukaan muuttujat voivat olla:

-Kategorinen

-Numeerinen

Kategoriset muuttujat, joita kutsutaan myös laadullinen, Ne edustavat sellaisia ​​ominaisuuksia, kuten henkilön siviili, joka voi olla yksin, naimisissa, eronnut tai leski.

Toisaalta numeeristen muuttujien tai kvantitatiivinen, Ne voidaan mitata, kuten ikä, aika, paino, tulot ja muut.

Grafiikat ovat erittäin tärkeitä tiedon esittämiseksi, koska yhdellä silmäyksellä tietojen kehitys arvostetaan. Lähde: Piqsels.

Erilliset ja jatkuvat muuttujat

Diskreettiset muuttujat ottavat vain erilliset arvot, kuten nimi viittaa. Esimerkkejä heistä ovat perheen lasten lukumäärä, kuinka monta koehenkilöä on tietyssä kurssissa ja pysäköintialueen autojen määrä.

Nämä muuttujat eivät aina ota kokonaisia ​​arvoja, koska on myös fraktioita.

Toisaalta jatkuvat muuttujat myöntävät äärettömiä arvoja tietyllä alueella, kuten ihmisen paino, veren pH, puhelinkonsultoinnin aika ja jalkapallopallojen halkaisija.

Voi palvella sinua: Symmetria

Keskeisen taipumuksen mittaukset

Anna käsitys siitä, että tiedot seuraavat yleisestä kehityksestä. Mainitsemme kolme eniten käytettyä keskustoimenpitoa:

-Puoli

-Mediaani

-Muoti

Puoli

Vastaavat keskiarvoja. Se lasketaan lisäämällä kaikki havainnot ja jakamalla kokonaismäärän välillä:

 Missä x_Yllyttää Se on mikä tahansa havainto ja n on niiden kokonaismäärä.

Muoti

Se on arvo, joka toistetaan eniten tietojoukossa, yleisin, koska jakautumisessa voi olla enemmän kuin yksi muoti.

Mediaani

Tietojoukkoa tilaamalla mediaani on kaikkien keskeinen arvo.

Dispersion mitat

He huomauttavat tietojen vaihtelun ja antavat kuvan siitä. Eniten käytettyjä ovat:

Etäisyys

Se on ero suurimman arvon x välillä_M ja pienin x_m tietojoukosta:

Alue = x_M - x_m

Varianssi

Mittaa kuinka pitkälle keskimääräiset arvotiedot ovat. Tätä varten tehdään keskimäärin, mutta minkä tahansa arvon välillä on eroja_Yllyttää ja keskiarvo, neliö estää niitä peruuttamasta toisiaan. Sitä merkitään yleensä kreikkalaisella kirjaimella σ neliö tai S: n kanssa²-

Keskihajonta

Varianssissa ei ole samoja yksiköitä kuin data, joten standardipoikkeama määritellään varianssin neliöjuuriksi ja sitä merkitään nimellä σ tai s:

Taajuusjakaumat

Sen sijaan, että otetaan huomioon jokainen tieto erikseen, on edullista ryhmitellä ne alueille, mikä helpottaa työtä, varsinkin jos arvoja on monia. Esimerkiksi työskennellessäsi koulun lasten kanssa heidät voidaan ryhmitellä ikäryhmiin: 0–6 vuotta, 6–12 vuotta ja 12-18 vuotta.

Kaaviot

Ne ovat erinomainen tapa arvostaa näkymätietojen jakamista ja sisältävät kaikki taulukoihin ja kuviin kerätyt tiedot, mutta paljon edullisempia.

Niitä on laaja valikoima: tankojen, lineaaristen, pyöreiden, varren ja lehtien, histogrammien, taajuuden polygonien ja pikakävien kanssa. Esimerkkejä tilastollisista kuvaajista on esitetty kuvassa 3.

Kiinnostavia teemoja

Tilasto.

Tilastolliset muuttujat.

Väestö ja otos.

Päätelmätilastot.

Viitteet

1. Faraldo, P. Tilastot ja tutkimusmenetelmät. Palautettu: eio.USC.On.
2. Fernández, S. 2002. Kuvailevia tilastoja. Toinen. Painos. ESIC -toimitus. Palautettu: Google Books.
3. Tilastohistoria. Toipunut: Eumed.netto.
4. Ibañez, s. 2010. Matematiikka II. Pätevyyslähestymistapa. Cengage -oppiminen.
5. Monroy, S. 2008. Kuvailevia tilastoja. Ensimmäinen. Painos. Meksikon kansallinen ammattikorkeakoulutus.
6. Maailmankaikkeuden kaavat. Kuvailevia tilastoja. Toipunut: UniversOformulat.com.