Arviointi väliajoin

Mikä on arviointia välein?

Se Arviointi väliajoin Se on tapa määrittää arvoalue, johon populaation keskiarvo voidaan sisällyttää, äärellisen koon näytteen tietoihin, jotka on satunnaisesti poistettu kokonaispopulaatiosta.

Hän Arviointiväli Se on alhaisempi, koska näyte on suurempi, mutta se tulee laajemmaksi, jos samojen luotettavuuden taso tai prosentuaalinen osuus kasvaa.

Jos haluat tietää tietyn muuttujan väestön keskiarvon tarkkaan muodossa, niin väestöä tulisi harkita, jotain, joka ei ole aina mahdollista, koska jos se on erittäin suuri väestö, on kallista saada tietoa koko väestö. Tästä syystä yhden tai useamman satunnaisen näytteen kokonaispopulaatiosta käytetään.

Se perustuu hypoteesiin, että purkamalla satunnainen näyte, joka ei ole puolueellinen ja ottaen huomioon suhteellisesti kaikki kerrokset, näytteen keskiarvon on oltava hyvin lähellä populaation keskiarvoa.

Logiikka osoittaa, että mitä suurempi näytetiedot ovat keskimääräisen näytteen arvon ja keskimääräisen populaation arvon välillä.

Arviointiväli

Käytännössä, ellei täydellistä väestöä tunneta, on mahdollista löytää vain jonkin verran todennäköisyyttä, josta väestö keskiarvoa voidaan löytää, äärellisen koon otoksen perusteella.

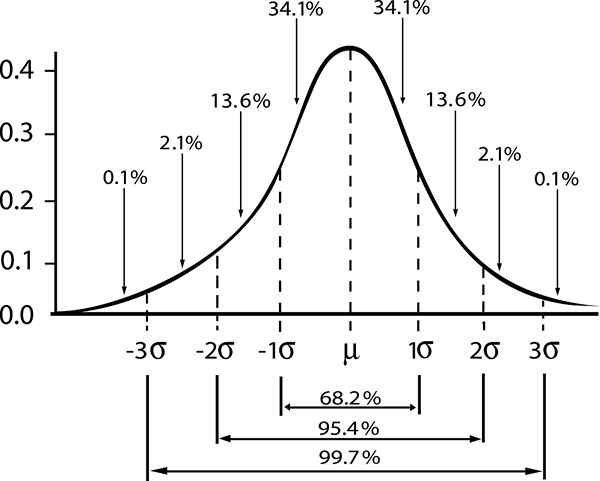
Normaalia jakautumista seuraavan populaation tapauksessa Keskihajonta σ , se Vakioero Väestön keskiarvo μ ja keskimääräinen kokoinen näyte n on annettu:

| μ - | ≤ σ / √n

Tässä sana "standardi" osoittaa, että 68% koonäytteistä n, Niillä on keskiarvo välin välillä [μ - σ / √n, μ + σ / √n].

Voi palvella sinua: Jakokelpoisuuskriteerit: mitkä ne ovat, mitkä ovat käyttö ja säännöt

Vakioarvio

Edellä mainitun vaihtoehtoinen tulkinta olisi sanoa, että populaation keskiarvo on saatu koon otoksesta n ja keskiarvo ymmärretään aikavälillä  [ - σ / √n, + σ / √n], 68%: n todennäköisyydellä.

Useimmissa todellisissa tapauksissa ei ole mahdollista tietää tavanomaista väestön poikkeamaa, niin σ Sitä arvioidaan näytteen keskihajonnalla s, joka lasketaan seuraavasti:

S = √ (∑ (x_Yllyttää - -A² / √ (N-1).

Sieltä saat välin, joka voisi sisältää väestön keskiarvon 68%: n luottamustasolla (tavanomainen luottamustaso), antamalla:

  -s / √n ≤ μ ≤ + s / √n

Tämä väestön mittausväli tunnetaan nimellä vakioarviointiväli ja saatiin vain käytettävissä olevilla tiedoilla n.

Edellisestä kaavasta seuraa, että jos halusit vahvistaa arviointiväliä puoleen, se on välttämätöntä nelinkertaistaa Näytteen koko.

Arvio luottamusvälein

Tietyissä tutkimuksissa standardi 68% voi olla riittämätöntä, niin on välttämätöntä määrittää väliarvot mielivaltaisella luottamustasolla γ.

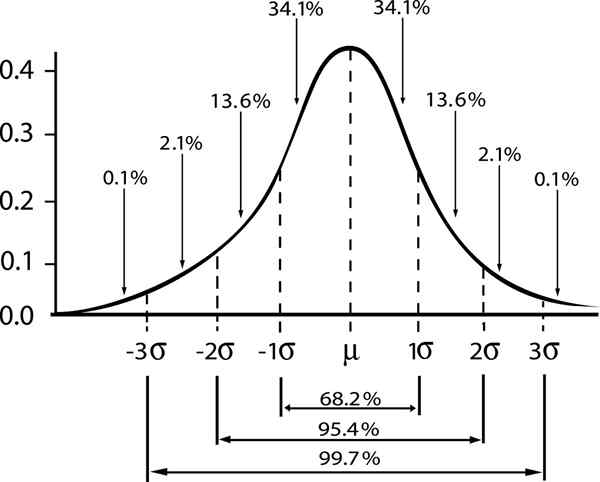Luotettavuuden marginaalin ja Gaussin jakauman välin välinen suhde on esitetty

Jos tarkoitamme ε Vakiovirhe s/√n, sitten luotettavuustason arviointivirhe γ annetaan:

E = zy⋅ε.

Missä Zy Se on numero, jolla vakiovirhe kerrotaan, ja siten saa virhemarginaali mielivaltaisella luottamustasolla γ.

Saada tekijä Zy, Jatka seuraavasti:

Se voi palvella sinua: rationaaliset numerot: Ominaisuudet, esimerkit ja toiminnot

Vaihe 1

On puhelu merkitsevyystaso α Vastaa luottamuksen tasoa γ seuraavan kaavan mukaan:

α = 1 - γ

Vaihe 2

Arvo määritetään:

Tämä on kertynyt taajuus tyypillisessä normaalissa jakaumassa N (0,1) Aikavälillä (-∞, Zy -.

Vaihe 3

Se puhdistuu Zy Yhtälö:

N (zy) = 1 - α/2

Koska se on olennainen yhtälö, tämä puhdistuma saadaan normaalijakaumataulukoista lineaarista interpolointimenetelmää käyttämällä.

Vaihe 4

Vaihtoehtoisesti taulukoiden käyttöön, laskentataulukoihin sisällytetyt tilastolliset toiminnot, kuten Excel, jompikumpi Google -arkki. Nämä ohjelmat sisältävät normaalin käänteisen toiminnon N^-1, niin että korjauskerroin Zy Se saadaan suoraan tämän käänteisen toiminnon arviointi:

Zy = n^-1(1 - α/2).

Tyypilliset luottamusvälit

Yleisimmin käytetyt luottamustasot ovat:

• Zy = 1; tavanomainen luottamustaso γ = 0,68.
• Zy = 2; luottamustaso γ = 0,95 (tai merkitsevyystaso 5%).
• Zy = 3; luottamustaso γ = 0,997 (tai 0,3%merkitsevyystaso)

Esimerkit

Esimerkki 1

Määritä vastasyntyneiden keskimääräinen painoväli elokuun aikana suuressa kaupungissa, joka perustuu 100 vauvan satunnaiseen näytteeseen, jossa saatiin keskimääräinen paino 3100 grammaa näytteen standardipoikkeamalla s = 1500 grammaa.

Ratkaisu

Ensinnäkin näytteen vakiovirhe määritetään:

ε = s/√n = (1500 g)/√100 = 150 g.

Siksi tästä näytteestä alkaen voidaan päätellä, että elokuussa syntyneiden vauvojen keskimääräinen paino kyseisessä kaupungissa on välillä 2950 g - 3250 g, 68%: n todennäköisyydellä.

Esimerkki 2

Oletetaan. Keskimääräinen näytteen paino on 3100 g tavanomaisella 1500 g dispersiolla. 

Se voi palvella sinua: Luonnollisten lukujen hajoaminen (esimerkit ja harjoitukset)

Tätä uudesta näytteestä pyydetään arvioimaan kyseisen kaupungin vastasyntyneiden keskimääräinen painoväli.

Ratkaisu

Nyt vakiovirhe pienenee tekijässä 1/√2, Joten keskimääräisen painon uusi vakiovirhe on 106 g.

Sitten tästä uudesta näytteestä voidaan arvioida, että vastasyntyneiden keskimääräinen paino koostuu välillä 2994 g - 3206 g, 68%: n todennäköisyydellä.

Harjoitukset

Harjoitus 1

Määritä vastasyntyneiden keskimääräinen painoalue elokuussa, esimerkissä 1 määritetystä näytteestä, 95%: n todennäköisyydellä.

Ratkaisu

95%: n luotettavuustaso kaksinkertaistaa keskimääräisen painoalueen, verrattuna 68%: n luotettavuustasoon.

Siksi vastasyntyneiden keskimääräinen paino sisältyy 2800 gramman alueelle 3400 grammaa 95%: n varmuudella.

Harjoitus 2

Arvio 99,7%: n luotettavuustasolla, jonka välein löydetään vastasyntyneiden keskimääräinen paino suuresta kaupungista, jos näyte on saatavana, jonka keskimääräinen paino on 100 3100 g ja vakionäytteen poikkeamalla s = 1500 g.

Ratkaisu

Keskimääräinen painovirhemarginaali, jolla on 99,7% varmuudesta, on kolminkertainen keskimääräinen virhe, toisin sanoen:

3*1500/√100.

Sitten tästä näytteestä päätellään, että vastasyntyneiden keskimääräinen paino sisältyy aikaväliin: 2650 grammaa - 3550 grammaa, varmuuden taso 99,7%. 

Tästä tuloksesta havaitaan, kuten suuremmalla varmuuden tasolla lisää keskimääräisen painon epävarmuutta paljon laajempaan väliaikaiseen väliajoin.