Prosenttivirhe
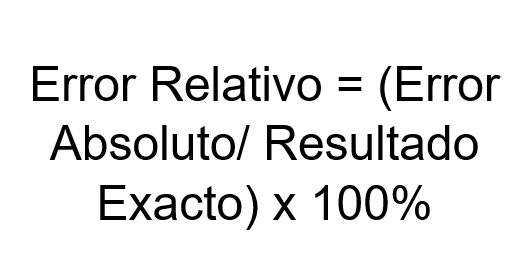
- 1439
- 269
- Dr. Travis Reichert
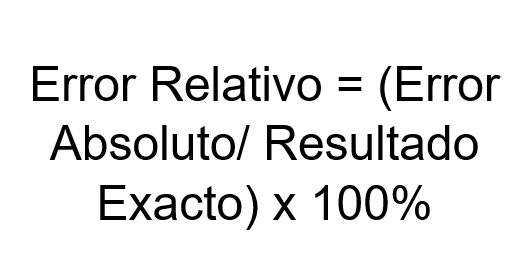
Mikä on prosentuaalinen virhe?
Hän prosenttivirhe Se on suhteellisen virheen osoitus prosentuaalisesti. Toisin sanoen, se on numeerinen virhe, joka ilmaistaan arvolla, joka antaa suhteellisen virheen, myöhemmin kerrottuna 100: lla.
Ymmärtääksesi, mikä on prosenttivirhe, sinun on ensin ymmärrettävä, mikä numeerinen virhe, absoluuttinen virhe ja suhteellinen virhe, koska prosentuaalinen virhe on johdettu näistä kahdesta termistä.
Numeerinen virhe on sellainen, joka ilmestyy, kun mittaa otetaan epäselvästi laitetta käytettäessä (suora mittaus) tai kun matemaattinen kaava (epäsuora mitta) käytetään huonosti.
Kaikki numeeriset virheet voidaan ilmaista ehdottomasti tai prosenttiosuus. Absoluuttinen virhe on puolestaan, joka tapahtuu suoritettaessa lähestymistapaa edustaakseen matemaattista määrää, joka johtuu elementin mittauksesta tai kaavan virheellisestä soveltamisesta.
Tällä tavoin lähestymistapa muuttaa tarkkaa matemaattista arvoa. Absoluuttisen virheen laskeminen tapahtuu vähentämällä lähestymistapa tarkkaan matemaattiseen arvoon, kuten tämä:
Absoluuttinen virhe = tarkka tulos - lähestymistapa
Suhteellisen virheen osoittamiseen käytetyt mittayksiköt ovat samat, joita käytetään puhumaan numeerisesta virheestä. Samoin tämä virhe voi antaa positiivisen tai negatiivisen arvon.
Suhteellinen virhe on jakamalla jakamalla absoluuttinen virhe tarkalla matemaattisella arvolla.
Tällä tavoin prosentuaalinen virhe on se, mitä saadaan kertomalla suhteellisen virheen tulos 100. Toisin sanoen prosentuaalinen virhe on suhteellisen virheen prosentuaalinen (%) ilmaisu.
Voi palvella sinua: x SquaredSuhteellinen virhe = (absoluuttinen virhe/ tarkka tulos)
Prosenttiosuus, joka voi olla negatiivinen tai positiivinen, ts. Se voi olla arvo, jota edustaa ylimääräinen tai oletusarvo. Tämä arvo, toisin kuin absoluuttinen virhe, ei esiinny yksiköitä prosentuaalisen määrän ulkopuolella (%).
Suhteellinen virhe = (absoluuttinen virhe/ tarkka tulos) x 100%
Suhteellisten ja prosentuaalisten virheiden tehtävänä on osoittaa jonkin laatu tai tarjota vertaileva arvo.
Esimerkkejä prosentuaalisen virheen laskemisesta
1. Kaksi -Land -mittaus
Mittaamalla kaksi erää tai maata sanotaan, että mittauksessa on noin 1 m virhe. Maa on 300 metriä ja toinen 2: sta.000.
Tässä tapauksessa ensimmäisen mittauksen suhteellinen virhe on suurempi kuin toisen, koska suhteessa 1 m edustaa suurempaa prosenttia.
300 m erä:
EP = (1/300) x 100%
EP = 0,33%
Paljon 2.000 m:
EP = (1/2.000) x 100%
EP = 0,05%
2. Alumiinimittaus
Laboratoriossa toimitetaan alumiinilohko. Kun mitataan lohkon mitat ja laski sen massa ja tilavuus, sen tiheys määritetään (2,68 g/cm³).
Kun tarkistetaan materiaalin numeerista taulukkoa, tämä osoittaa kuitenkin, että alumiinitiheys on 2,7 g/cm³. Tällä tavalla absoluuttinen ja prosentuaalinen virhe lasketaan seuraavasti:
EA = 2,7 - 2,68
EA = 0,02 g/cm³.
EP = (0,02/2,7) x 100%
EP = 0,74%
3- Osallistuminen tapahtumaan
Oletettiin, että 1.000.000 ihmistä menisi tiettyyn tapahtumaan. Tähän tapahtumaan menneiden ihmisten tarkka lukumäärä oli kuitenkin 88.000. Absoluuttinen ja prosentuaalinen virhe olisi seuraava:
Voi palvella sinua: satunnaismuuttuja: käsite, tyypit, esimerkitEA = 1.000.000 - 88.000
EA = 912.000
EP = (912 000/1 000 000) x 100%
EP = 91,2%
4. Pallo pudota
Lasketun ajan on otettava pallo päästäkseen maahan sen jälkeen, kun ne heitetään 4 metrin etäisyydellä, on 3 sekuntia.
Kokeiluhetkellä havaitaan kuitenkin, että pallo kesti 2,1 sekuntia päästäkseen maahan.
EA = 3 - 2,1
EA = 0,9 sekuntia
EP = (0,9/2,1) x 100%
EP = 42,8%
5. Auton saapuminen vie
Arvioidaan, että jos auto menee 60 km, se saavuttaa määränpäänsä tunnissa. Todellisessa elämässä auto kuitenkin kesti 1,2 tuntia määränpäähänsä. Tämän ajanlaskelman prosentuaalinen virhe ilmaistaan seuraavasti:
EA = 1 - 1,2
Ea = -0,2
EP = (-0,2/1,2) x 100%
EP = -16%
6. Mittauspituus
Mikä tahansa pituus mitataan arvolla 30 cm. Tämän pituuden mittauksen varmistaminen on selvää, että virhe oli 0,2 cm. Prosenttivirhe tässä tapauksessa ilmenee seuraavasti:
EP = (0,2/30) x 100%
EP = 0,67%
7. Sillan pituus
Sillan pituuden laskeminen sen tasojen mukaan on 100 metriä. Kun vahvistetaan tämä pituus, kun se on rakennettu, on kuitenkin selvää, että se on oikeastaan 99,8 m pitkä. Prosenttivirhe todistetaan tällä tavalla.
EA = 100 - 99,8
Ea = 0,2 m
EP = (0,2/99,8) x 100
EP = 0,2%
8. Ruuvin halkaisija
Vakiovalmistetun ruuvin pää on halkaisijaltaan 1 cm.
Voi palvella sinua: jatkuva yhtenäinen jakauma: ominaisuudet, esimerkit, sovelluksetTätä halkaisijaa mitattaessa havaitaan kuitenkin, että ruuvipään on todella 0.85 cm. Prosenttivirhe olisi seuraava:
EA = 1 - 0,85
EA = 0,15 cm
EP = (0,15/0,85) x 100
EP = 17,64%
9. Esinepaino
Sen tilavuuden ja materiaalien mukaan arvioidaan, että tietyn esineen paino on 30 kiloa. Kun esine on analysoitu, havaitaan, että sen todellinen paino on 32 kiloa.
Tässä tapauksessa prosentuaalisen virheen arvo kuvataan seuraavasti:
EA = 30 - 32
Ea = -2 kiloa
EP = (2/32) x 100
EP = 6,25%
10. Teräsmittaus
Laboratoriossa tutkitaan teräslevyä. Kun mitataan arkin mitat ja laske sen massa ja tilavuus, määritetään saman tiheys (3,51 g/cm³).
Kun tarkistetaan materiaalin numeerista taulukkoa, tämä osoittaa kuitenkin, että teräksen tiheys on 2,85 g/cm³. Tällä tavalla absoluuttinen ja prosentuaalinen virhe lasketaan seuraavasti:
EA = 3,51 - 2,85
EA = 0,66 g/cm³.
EP = (0,66/2,85) x 100%
EP = 23,15%
Viitteet
- Prosenttivirhe. Toipunut MathSisfunista.com
- Kuinka laskea prosentuaalinen virhe. Toipunut Ajatelukyvystä.com

