Hypoteesin testaus

Mikä on hypoteesitesti?

Se hypoteesin testaus, Tilastoissa se on menettely, jota käytetään tarkistamaan, kuinka onnistunut arvaus on a väestö. Näitä oletuksia kutsutaan hypoteesi, että periaatteessa niitä pidetään totta, kunnes jotkut todisteet vahvistavat tai kiistävät sen.

Nämä todisteet toimittavat näytetiedot, ne, jotka tulevat merkittävän osan väestöstä, nimeltään näyte. Todennäköisyysteoria tarjoaa tarvittavat tekniikat hypoteesien todenmukaisuuden vastaamiseksi.

Esimerkkejä hypoteeseista ovat:

-Ihmisen keskimääräinen kehon lämpötila on 36.1 ºC.

-Välipala -tehtaalla tuotettu suolainen maapähkinäpussi painaa keskimäärin 50 g.

-80% kaupungin asukkaista teki ostoksia verkossa viimeisen 6 kuukauden aikana.

-IQ -testitulokset yliopisto -opiskelijoille tunnetuista laitoksista, keskihajonta on 15.

-Tietty satunnaismuuttuja x seuraa Poisson -jakautumista.

Ensimmäiset neljä ovat hypoteesin tyyppiä parametrinen, Koska nämä ovat lausuntoja joistakin populaatioparametrista, kuten keskimääräinen, keskihajonta tai jokin osuus.

Toisaalta viimeinen hypoteesi määrittää satunnaismuuttujan jakauman, ja koska se ei viittaa mihinkään populaation parametriin tai ominaisuuteen, sanotaan, että se on hypoteesi ei parametrinen.

Nollahypoteesi ja vaihtoehtoinen hypoteesi

On olemassa kahden tyyppisiä hypoteeseja, joiden avulla testi suorittaa, mikä vastaa niitä:

-Nollahypoteesi, nimeltään h_{0 -}, toteaa, että tutkittavalla parametrilla on vakiintunut arvo tai että satunnaismuuttuja seuraa tiettyä jakaumaa. Siksi ilmaisemalla symbolisesti nollahypoteesia, tasa -arvon symbolia käytetään aina.

-Vaihtoehtoinen hypoteesi: nimeltään h₁, Hän väittää, että parametri tai jakauma eroa.

Se voi palvella sinua: Algebra -lukon ominaisuus: esittely, esimerkit

Kun nollahypoteesi hyväksytään, vaihtoehtoinen hypoteesi hylätään, joten molemmat ovat toisiaan poissulkevia.

Merkitsevyystaso

Se on virheen mitta, joka voidaan tehdä hypoteesitestin suorittamisessa. Se määritellään todennäköisyytenä hylätä nollahypoteesi, koska se on totta. Se on yleensä merkitty kreikkalaisella kirjaimella α:

α = p (hylkää H_{0 -} Kun se on totta)

Α: lle yleisesti käytetyt arvot ovat 0.01, 0.05 ja 0.10; on toinen yleisin käyttö. Vastaavasti vastaavasti 1%, 5% ja 10%: n todennäköisyys tehdä virheitä, kun hylätään H_{0 -}, Mutta joka tapauksessa, mitä alhaisempi merkitsevyystaso, sitä luotettavampi testitulos.

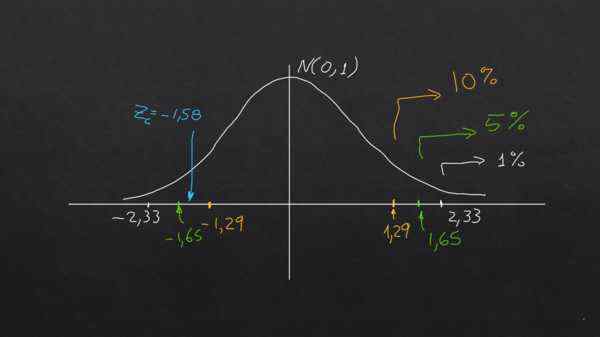
Alfa -arvo (α) voidaan ymmärtää oikean hännän (tai vasemman) pinta -alan prosenttiosuutena tyypillisessä (μ = 0 ja σ = 1) ja nämä arvot tapahtuvat aina z = 2,33 α: lla = 0.01; at z = 1,65 α = 1,65 ja z = 1,29 α = 0,1: lle.

Vaiheet hypoteesitestin suorittamiseksi

Vaihe 1

Määritä vastaavasti nolla- ja vaihtoehtoiset hypoteesit. Nollahypoteesi osoittaa, että tutkittavan θ: n nimeltä θ_{0 -}-

H_{0 -}: θ = θ_{0 -}

Esimerkiksi, jos lääkkeen vaikutuksia tutkitaan laboratoriohiirien populaation tietyllä ominaispiirteellä, nollahypoteesissa harkitaan, että tällä lääkkeellä ei ole merkitystä tällaisessa ominaispiirteessä ja että tällä on vakioarvo θ_{0 -}.

Nollahypoteesin symbolisoimiseksi tasa -arvon merkkiä käytetään aina, toisaalta vaihtoehtoinen hypoteesi käyttää yhtä symboleja tai ≠.

Lääkkeen esimerkissä vaihtoehtoinen hypoteesi osoittaa, että yhdisteellä on jonkin verran vaikutusta kyseiseen ominaisuuteen. Siksi tämä on suurempi, alempi tai yksinkertaisesti erilainen kuin referenssiarvo θ_{0 -}.

Voi palvella sinua: tekijän merkinnät: Konsepti, esimerkit ja harjoitukset

Vaihe 2

Valitse sopiva merkitsevyystaso, joka yleensä vahvistetaan 5 %: lla, kuten aiemmin ilmoitettiin.

Vaihe 3

Määritä populaatio ja ote siitä näyte tai näytteet, joiden analyysi vastaa hypoteeseja ja määrittämään nollahypoteesin hyväksyminen tai hylkääminen.

Vaihe 4

Valitse ja laske kerättyjen tietojen tutkimustilastojen arvo, josta saadaan tarvittavat todisteet päätöksen tekemiseksi nollahypoteesin hyväksymisestä tai hylkäämisestä. Koetilastojen valinta riippuu valitusta parametrista: keskiarvo, poikkeama, osuus tai muu.

Koetilastot saadaan muuntamalla näyteparametri Z -pistemääräksi, opiskelija-, R Pearson- tai Chi -neliötilastoksi, valitun kokeellisen suunnittelun mukaan. Tälle on kaavoja.

Yleensä, jos populaatioparametri on keskimääräinen μ, ”x -palkki” on näytteen keskiarvo, keskihajonta σ tunnetaan ja näytteen koko on n> 30, testitilasto z_C Se lasketaan Z -pisteellä:

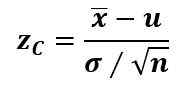
Ja kun n < 30, pero σ es desconocida, se usa la t de Student.

Vaihe 5

Aseta kriteerit nollahypoteesin hyväksymis- tai hylkäämiselle, joka voidaan tehdä kahdella menettelyllä:

• P -arvojen kautta.
• Verrattuna kriittisiin arvoihin.

P -arvot vastaavat havaittujen tulosten saamisen todennäköisyyttä, koska nollahypoteesi on totta. Jos nämä arvot ovat pieniä, nollahypoteesi hylätään, jos niitä ei ole, se hyväksytään. Joka tapauksessa P -arvot eivät ole todisteita siitä, että vaihtoehtoinen hypoteesi on totta.

On otettava huomioon, että hypoteesitestissä on mahdollista tehdä kahden tyyppinen virhe:

• Tyyppi I virhe: Hylkää h_{0 -} Kun se on totta. Sen todennäköisyys on α ja vastaa todisteiden merkityksen tasoa.
• Tyypin II virhe: Hyväksy h_{0 -} Kun se on todella väärä. Sen todennäköisyys merkitään nimellä β.

Se voi palvella sinua: mikä on Rhombus -alueen ja suorakulmion välinen suhde?

Vaihe 6

Tehdä päätös hyväksyä tai hylätä nollahypoteesi. Jos käytetään P: n arvoja, kun p < α, se rechaza H_{0 -} Ja H hyväksytään₁, Ja muuten H hyväksytään_{0 -}. P -arvojoukko < α se conoce como kriittinen alue. Jos tilastot ovat tällä aikavälillä, H hylätään_{0 -}.

Samoin valittiin kriittinen arvo, valitun populaatioparametrin mukaan. Jos tämä on keskiarvo, jatka seuraavasti:

• Hännän testi: θ < θ_{0 -} tai θ> θ_{0 -}
• Kaksi pyrstötesti: | θ | < θ_{0 -}

Ratkaistu esimerkki

Kone valmistaa ruuveja, joiden nimellisen arvon on oltava 800 millimetriä pitkä, ja keskihajonta on 5%.

Otetaan satunnainen näyte, ts. Kun näytteen keskimääräinen pituus lasketaan, saadaan 790 millimetrin arvo.

Määritä, onko keskimääräinen pituus toleranssilla merkitsevyystasojen kanssa vastaavasti 1%, 5% ja 10%.

Ratkaisu

Ensimmäinen on laskea keskimääräinen testitilasto, joka tässä tapauksessa on jaetun keskiarvon poikkeama tavanomaisen populaatiovirheen välillä:

Zc = (790 - 800) / (40 / √40) = -1,58

Jos on otettu huomioon, että 5%: n keskihajonta vastaa 40: tä 800: sta.

Nollahypoteesi on, että keskimääräinen näyte on toleranssin sisällä vaadittavalle merkitsevyystasolle, edellyttäen, että | ZC | on pienempi kuin tyypillinen arvo | zt |, muuten nollahypoteesi hylätään.

1%: n ja 5%: n merkitsevyyden suhteen nollahypoteesi täyttyy, koska | ZC | < 2,33 y |Zc| < 1,65 respectivamente.

10%: n merkityksessä tapahtuu kuitenkin, että | ZC | > 1.29. Toisin sanoen tällä merkityksellisellä tasolla nollahypoteesi ei täyty.

Seuraava kaavio selventää johtopäätöstä:

Kaavio näkyy, kun vaadittu merkitsevyystasosta riippuen, sama hypoteesi voidaan hyväksyä tai hylätä samalla datalla. Lähde: f. Zapata.