Toimintojen arviointi

Arvioidakseen funktion, jonka kaavio tunnetaan tietylle aloitusjoukon arvolle tai elementille, se riittää tarkkailemaan vastaavaa elementtiä saapumisjoukossa. Lähde: f. Zapata.

Mikä on toimintojen arviointi?

Se Toimintojen arviointi Se koostuu tietyn verkkotunnuksen kuvan määrittämisestä. Toisin sanoen aloitusjoukon tietylle arvolle sinun on löydettävä sen vastaava saapumisjoukosta.

Toiminto voidaan edustaa monin tavoin. Jos esimerkiksi Venn -kaavio on saatavana, arviointi on hyvin yksinkertainen, se riittää valitsemaan lähtö- tai verkkotunnuksen elementti ja katso elementti, joka vastaa saapumisjoukkoa.

Edellä esitetty "…… on pääomaa kaaviota", kun arvioitaessa tätä toimintoa “Kanada” -elementtiä, se on “Ottawa” -elementti, jos se tapahtuu "Meksikon" kanssa, se on “Mexico City” ja pian.

Jos funktio annetaan siisteiden parien muodossa, arviointi on myös yksinkertainen: järjestetyn vääntömomentin toinen jäsen on ensimmäisen jäsenen kuva. Esimerkiksi funktion f (x) kanssa kuvailtu:

f (x) = (0,0); (1,2); (2,4); (3,6); (4,8); (5.10); (6,12)

Arvioitaessa arvoa 3, tulos on 6; Arvioitaessa 5 on 10 ja niin edelleen.

Samoin funktio voidaan arvioida, kun kaavio on käytettävissä, edellyttäen, että siinä oleva arvo näkyy siinä.

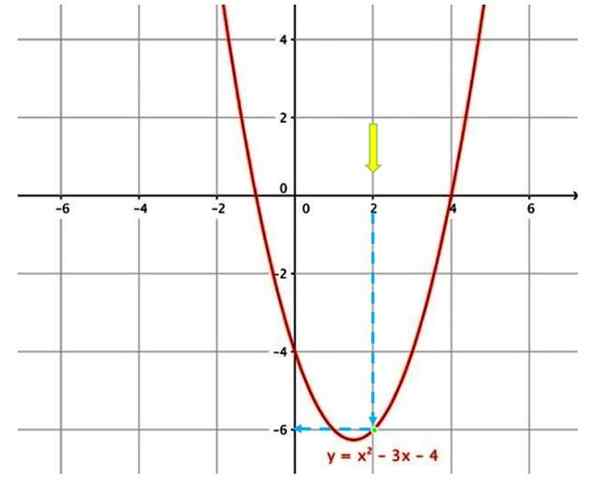Kaavio toiminnon arvioimiseksi

Esimerkiksi yllä esitetyn funktion arvioimiseksi x = 2: ssa on ensin paikantaa kuvaaja A x = 2 (keltainen nuoli).

Sitten sinun on liikuttava sinisen pystysuoran nuolen seurauksena, kunnes kosketat käyrää (vihreä piste). Seuraa sinistä nuolta uudelleen, mikä osoittaa vastaavan arvon pystysuoralla akselilla, siksi saadaan funktiota x = 2, y = −6.

Se voi palvella sinua: trigonometriset toiminnot: Basic, Cartesian tasossa, esimerkkejä, liikunta

Arvioi tietty funktio matemaattisessa merkinnässä

Yllä olevan kaavion alaosassa graafinen funktio ilmestyy, mutta annetaan matemaattisessa merkinnässä, ts. Kaavan kautta:

f (x) = x² - 3x - 4

Kun haluat arvioida funktion missä tahansa arvossa x = a, sinun on löydettävä f (a), joka yksinkertaisesti luetaan "f: n".

Tuloksen löytämiseksi x = a korvataan funktiokaavassa, ja siellä suoritetaan pyydetyt toiminnot ja laskelmat.

Oletetaan, että haluat arvioida esimerkin funktiota x = −1. Tämä tarkoittaa, että F (−1) on löydettävä.

Ensimmäinen vaihe on korvata x = -1 toiminnossa:

f (−1) = (−1)² - 3 ∙ (−1) - 4

Ja sitten suorita ilmoitetut toiminnot, jotka tässä esimerkissä ovat:

• Etsi −1: n neliö: (−1)² = 1
• Vähennä tuotteen 3 ∙ (−1) edellinen arvo: 3 ∙ (−1) = −3
• Edellisestä tuloksesta vähennys 4

f (−1) = (−1)² - 3 ∙ (−1) - 4 = 1 + 3 - 4 = 0

Lukija voi vahvistaa tämän tuloksen funktion kuvaajasta.

Kuvattuja menettelytapoja voidaan käyttää toiminnon arvioimiseen millä tahansa muulla verkkotunnuksella. Esimerkiksi, löydät F (-2), F (100) tai jopa F (H), josta H on mielivaltainen muuttuja, joka kuuluu funktion alueeseen.

Arvioi funktio arvolla x = h 

Oletetaan.

Tässä tapauksessa X korvataan h: llä, samalla tavalla kuin se tehdään, kun x saa numeerisen arvon, ja tulos yksinkertaistetaan niin paljon kuin mahdollista.

Kun tuloksena olevaa toimintaa ei enää voida yksinkertaistaa, tuloksena oleva toimenpide on jäljellä.

Se voi palvella sinua: Enegon: Ominaisuudet, miten tehdä enegon, esimerkkejä

Esimerkki

Haluat arvioida funktion f (x) = x² - 3x - 4 at x = h+1. Tarvittava lähestymistapa on seuraava:

F (H+1) = (H+1)² - 3 ∙ (H+1) - 4

Tasa -arvon oikealla puolella ensimmäinen termi on merkittävä tuote:

(H+1)² = h² +2H + 1

Seuraava termi ratkaistaan ​​jakavan ominaisuuden avulla:

3 ∙ (H + 1) = 3H + 3

Kun korvaat kaikki yllä olevat, sinulla on:

F (H+1) = (H+1)² - 3 ∙ (H+1) - 4 = H² +2H + 1 - (3H + 3) - 4

Samanlaisia ​​termejä pienennetään algebrallisella summalla:

f (h+1) = h² + 2H + 1 - 3H - 3 - 4 = H² - H - 6

Differentiaali

Funktion f (x) erojen differentiaalinen osuus tai suhde d määritetään seuraavasti:

Kunto H ≠ 0, mikä on välttämätöntä, koska jakoa 0: lla ei ole määritelty.

Tätä osamäärää tulkitaan geometrisesti kuin käyrän välisen viivan kaltevuus, ts. Näiden pisteiden koordinaatit ovat: [x, f (x)] ja [x+h; f (x+h)], kuten seuraavassa kuvassa nähdään:

Differentiaaliosamäärä vastaa Secant -viivan kaltevuuden laskemista käyrälle, joka kulkee ilmoitettujen pisteiden läpi. Lähde: Wikimedia Commons.

Siksi tämä osamäärä esiintyy funktion johdannaisen laskennassa, koska H -lähestymistapa arvon 0, secant -viivasta on taipumus tulla tangenttiviivaksi pisteessä (x, y), koska pisteistä risteyksessä on risteyksessä luku on niin lähellä, että niillä on taipumus samaan kohtaan.

Siten linjasta tulee tangentti (katkaisee käyrän yhdessä pisteessä).

Tämä on juuri funktion johdettu määritelmä: koordinaattipisteen käyrän tangentin kaltevuus (x, f (x))).

Se voi palvella sinua: Painotetut media: miten se lasketaan, esimerkkejä ja harjoituksia

Kuten voidaan nähdä, differentiaaliosamäärä vaatii toiminnon arvioinnin (x + h) ja x: ssä. Seuraavat esimerkit kuvaavat kuinka se tehdään.

Esimerkki 1

Haluat löytää funktion f (x) = 2x - 3 differentiaaliosaston. Ensimmäinen vaihe on nostaa funktion arviointi x = x + H, kuten tämä:

f (x+h) = 2 ∙ (x+h) - 3 = 2x+2h - 3

Sitten tulos korvataan aiemmin annetun D: n määritelmässä:

H ≠ 0: n kanssa.

Osoittajaa yksinkertaistetaan niin pitkälle kuin mahdollista, vähentämällä samanlaisia ​​termejä:

Lopuksi, numeraattorin ja nimittäjän yleiset tekijät yksinkertaistetaan:

D = 2

Esimerkki 2

Löydä funktion f (x) = x differentiaaliosuus² - 3x - 4.

Jatkamme kuten edellisessä esimerkissä, etsimällä ensin F (x+H), korvaamalla tulos D: stä ja yksinkertaistaen maksimiarvoa:

f (x+h) = (x+h)² - 3 (x+h) - 4 = x² + 2HX + H² - 3x - 3H - 4

= 2x+H-3

Siksi:

D = 2x+H-3

Missä H ≠ 0.

Ratkaisut

Harjoitus 1

Arvioi funktio f (x) = 2x² - 4x + 1 kun:

a) x = -1
b) x = 0
c) x = 2

Liittää jhk

F (-1) = 2 (-1)² - 4 (-1) + 1 = 2 + 4 + 1 = 7

Ratkaisu b

F (0) = 2 (0)² - 4 (0) + 1 = 0 - 0 + 1 = 1

Liuos C

f (2) = 2 ∙ 2² - 4 ∙ 2 + 1 = 8 - 8 + 1 = 1

Harjoitus 2

Luonnonsuojelijatiimi päätti, että funktio w (t) = 0.lt² + 1.8T mallintaa "W" -jätteen määrän kilogrammissa, jotka heitetään tiettyyn jokeen, aikanaan "T", joka on annettu päivinä.

Laske jokeen heitetyn jätteen määrä:

a) 3 päivää
b) 1 viikko
c) 1 kuukausi

Liittää jhk

W (t) -toiminto arvioidaan t = 3 päivässä:

W (3) = 0.1 × 3² +1.8 × 3 = 0.9 + 5.4 = 6.3 kiloa

Ratkaisu b

Ennen arviointia, sinun on vietettävä 1 viikko päiviin:

1 viikko = 7 päivää

W (7) = 0.1 × 7² +1.8 × 7 = 4.9 + 12.6 = 17.5 kiloa

Liuos C

Jälleen on välttämätöntä muuttaa kuukaudet päiviksi:

1 kuukausi = 30 päivää

W (30) = 0.1 × 30² +1.8 × 30 = 90 + 54 = 144 kiloa

Viitteet

1. Larson, r. 2012. Ennakkoluulo. Kahdeksas. Painos. Cengage -oppiminen.
2. Monterey Institute. Toimintojen arviointi. Toipunut: Montereyinstitute.org.
3. Stewart, J. 2007. Precculment: Laskentamatematiikka. Viides. Painos. Cengage -oppiminen.
4. Sullivan, M. 1997. Ennakkoluulo. Neljäs. Painos. Pearson -koulutus.
5. Zill, D. 2008. Ennakkoluulo laskenta etenee. Neljäs. Painos. McGraw Hill.