Torricelli -kokeilun ilmakehän painekomentit, merkitys

Hän Torricelli -koe Sen suoritti italialainen fyysikko ja matemaatikko.

Tämä koe syntyi tarpeesta parantaa vesien tarjontaa kaupungeissa. Evankelista Torricelli (1608-1647), joka oli Toscana Fernando II: n Grand Duke -tuomarin matemaatikko, oli opiskellut Galileon kanssa hydraulisia ilmiöitä.

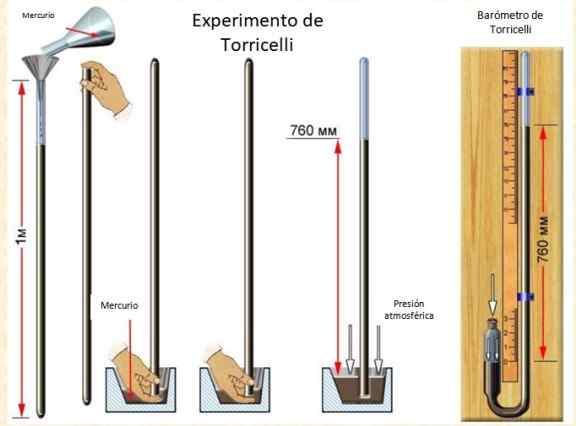
Kuvio 1. Torricellin koe, jossa elohopeapylväs on 760 mm ilmakehän paineen vuoksi. Lähde: f. Zapata.

[TOC]

Koe

Vuonna 1644 Torricelli teki seuraavan kokemuksen:

- Elohopea, joka otettiin käyttöön 1 m pituusputkessa, avoinna toisesta päästä ja suljettu toisella.

- Kun putki oli täysin täynnä, hän sijoitti sen ja kumosi sen astiaan, joka sisälsi myös elohopeaa.

- Torricelli havaitsi, että pylväs laski ja pysähtyi noin 76 cm korkealla.

- Hän tajusi myös, että vapaassa tilassa oli syntynyt tyhjiö, vaikkakaan ei täydellinen.

Torricelli toisti kokeen käyttämällä eri putkia. Hän jopa suoritti pienen variantin: hän lisäsi vettä kauhaan, joka oli kevyempi, kellui elohopeaan. Sitten putki, joka sisälsi elohopeaa veden pintaan, nosti hitaasti.

Sitten elohopea laski ja vesi kiipesi. Saatu tyhjiö, kuten olemme jo sanoneet, ei ollut täydellinen, koska elohopeaa tai vesihöyryä oli aina jäännöksiä.

Ilmakehän paineen mitta

Ilmapiiri on kaasujen seos, jossa typpi ja happi ovat vallitsevia, jäljet ​​muista kaasuista, kuten argonista, hiilidioksidista, vedystä, metaanista, hiilimonoksidista, vesihöyrystä ja otsonista.

Voi palvella sinua: Tähtien sade: muodostuminen, kuinka tarkkailla niitä, ominaisuudet

Maapallon käyttämä gravitaatiohanke on vastuussa koko ympäröivän planeetan pitämisestä.

Koostumus ei tietenkään ole tasainen eikä myöskään tiheys, koska se riippuu lämpötilasta. Pinnan lähellä on hyvä määrä pölyä, hiekkaa ja epäpuhtauksia luonnollisista tapahtumista ja myös ihmisen toiminnasta. Raskaimmat molekyylit ovat lähempänä maata.

Koska vaihtelua on niin paljon, on tarpeen valita ilmakehän paineen referenssi, joka on otettu merenpinnan tasoksi.

Tässä ei ole merenpinta, koska se esittelee myös vaihtelut. Taso o Narkina Apulla valitaan jotkut geodeettiset referenssijärjestelmät, jotka ovat asettaneet yhteisen sopimuksen välillä.

Kuinka paljon ilmakehän paine on lähellä maata? Torricelli löysi arvonsa, kun se mittasi sarakkeen korkeuden: 760 mm elohopeaa.

Torricelli -barometri

Putken yläosassa paine on 0, koska tyhjiö on muodostettu. Sillä välin, elohopean kylpyammeen pinnalla paine P₁ Se on ilmakehän paine.

Valitsemme viitejärjestelmän alkuperä elohopean vapaassa pinnassa putken yläosassa. Sieltä, kunnes saavut elohopean pinnan astiassa, se mitataan H, Pylvään korkeus.

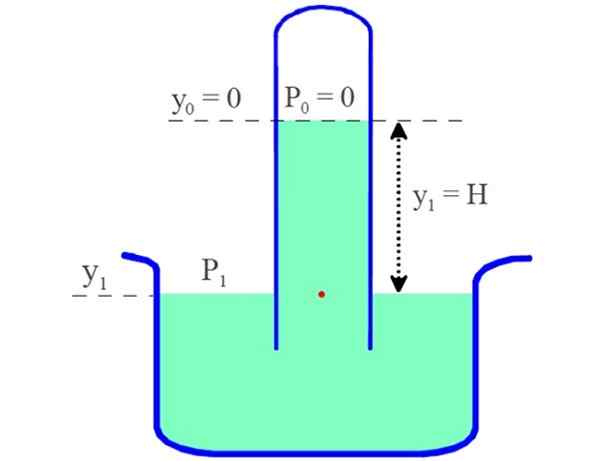Kuva 2. Torricelli -barometri. Lähde: Suunnittelijoiden yleinen fysiikka. J -. Asettaa. Laitos.

Paine punaisella merkittyyn pisteeseen syvyydessä ja₁ On:

P₁ = P_jompikumpi + ρ_Hg . g.ja₁

Missä ρ_Hg  Se on elohopean tiheys. Siitä asti kun ja₁ = H ja PO = 0-

P₁ = ρ_Hg . g.H

H = P₁/ ρ_Hg.g

Koska elohopean tiheys on vakio ja myös painovoima, osoittautuu, että elohopeapylvään korkeus on verrannollinen P_1, Mikä on ilmakehän paine. Tunnettujen arvojen korvaaminen:

Voi palvella sinua: mikä on jako fysiikassa?

H = 760 mm = 760 x 10 ^-3 m

G = 9.8 m/s²

ρ_Hg = 13.6 g /cc = 13.6 x 10 ³ kg/m³

P₁ = 13.6 x 10 ³ kg/m³ x 9.8 m/s² x 760 x 10 ^-3 M = 101.293 N/M²= 101.3 kN/m²

Kansainvälisen järjestelmän paineen yksikkö on Pascal, lyhennetty PA. Torricellin kokeen mukaan ilmakehän paine on 101.3 kPa.

Ilmakehän paineen merkitys ilmastolle

Torricelli havaitsi, että putken elohopeataso koki pieniä variaatioita päivittäin, joten hän päätteli, että ilmakehän paineen tulisi myös muuttua.

Ilmakehän paine on vastuussa suuresta osasta säästä, mutta sen päivittäiset vaihtelut jäävät huomaamatta. Se johtuu siitä, että ne eivät ole yhtä merkittäviä kuin myrskyjä tai kylmää, esimerkiksi.

Nämä ilmakehän paineen vaihtelut ovat kuitenkin vastuussa tuulista, jotka puolestaan ​​vaikuttavat sateisiin, lämpötilaan ja suhteelliseen kosteuteen. Kun maa kuumenee, ilma laajenee ja pyrkii nousemaan, aiheuttaen paineen vähentymisen.

Aina kun barometri osoittaa korkeita paineita, voit odottaa hyvää säätä, kun taas alhaisten paineiden ollessa on mahdollisuus myrskyihin. Ydinilmastoennusteiden tekemiseksi on kuitenkin tarpeen saada enemmän tietoa muista tekijöistä.

Hän Torr ja muut yksiköt painetta varten

Vaikka se kuulostaa oudolta, koska paine on määritelty voimana alueyksikköä kohti, meteorologiassa on pätevä ilmaista ilmakehän paine elohopean millimetreissä, kuten Torricelli vahvisti sen.

Se johtuu siitä, että elohopea -barometriä käytetään edelleen nykyään muutamalla variaatiolla siitä lähtien, niin että Torricellin kunniaksi 760 mm Hg on yhtä suuri kuin Torr. Toisin sanoen:

1 torr = 760 mm Hg = 30 tuumaa Hg = 1 Paine -ilmakehän = 101.3 kPa

Jos Torricelli olisi käyttänyt vettä elohopean sijasta, pylvään korkeus olisi 10.3 m. Mercury -barometri on käytännöllisempi olla kompakti.

Se voi palvella sinua: Big Bang -teoria: Ominaisuudet, vaiheet, todisteet, ongelmat

Muita laajennetun käytön yksiköitä ovat baarit ja millibaarit. Millibaari vastaa hehtopassalia tai 10² Pascales.

Korkeusmittarit

Korkeusmittari on instrumentti, joka osoittaa paikan korkeuden vertaamalla ilmakehän painetta siinä korkeudessa.

Jos korkeus ei ole kovin suuri, periaatteessa voimme olettaa, että ilman tiheys pysyy vakiona. Mutta tämä on lähestymistapa, koska tiedämme, että ilmakehän tiheys vähenee korkeuden myötä.

Edellä käytetyn yhtälön kautta käytetään ilmatiheyttä elohopean sijasta:

P₁ = P_jompikumpi + ρ_ilma . g.H

Tässä ilmaisussa P_jompikumpi Sitä pidetään ilmakehän paineena maaperän tasolla ja P1 Se on paikka, jonka korkeus määritetään:

H = (P₁ - P_jompikumpi) / ρ_ilma . g

Paineen vaihtelu korkeuden kanssa on parempia lähestymistapoja todellisuuteen eksponentiaalisella mallilla, jonka kautta korkeusyhtälö, Se yhdistää paikan ilmakehän paineen korkeudellaan:Missä P_jompikumpi Se on vertailupaine, normaalisti merenpinnan tasolla, P₁ on kyseisen paikan paine, H sen korkeus merenpinnan suhteen, ρ ilman tiheys merenpinnassa ja g Painovoiman arvo.

Korkeusmiehet osoittavat, että paine laskee eksponentiaalisesti korkeuden kanssa: H = 0, P₁= P_jompikumpi ja jos H → ∞, niin P₁=0 -.

Viitteet

1. Figueroa, D. 2005. Sarja: Tieteen ja tekniikan fysiikka. Nide 5. Nesteet ja termodynamiikka. Toimittanut Douglas Figueroa (USB).
2. Kirkpatrick, L. 2007. Fysiikka: Katsaus maailmaan. Kuudes lyhennetty painos. Cengage -oppiminen.
3. Makaa, j. 2004. Suunnittelijoiden yleinen fysiikka. Laitos.
4. Mott, r. 2006. Fluidimekaniikka. Neljäs. Painos. Pearson -koulutus. 
5. Strangeways, minä. 2003. Luonnollisen ympäristön mittaus. Toinen. Painos. Cambridge University Press.