Factoring

Mikä on tekijä?

Faktorisointi on menetelmä, jonka kautta polynomi ilmenee tekijöiden kertolaskennan muodossa, jotka voivat olla numeroita, kirjaimia tai molemmat. Tekijäksi termeille yhteiset tekijät on ryhmitelty, ja tällä tavalla polynomi hajoaa useissa polynomeissa.

Siten, kun tekijät lisääntyvät toistensa kanssa, tulos on alkuperäinen polynomi. Faktorointi on erittäin hyödyllinen menetelmä, kun algebrallisia lausekkeita on, koska siitä voi tulla useiden yksinkertaisten termien kertominen; Esimerkiksi: toinen² + 2AB = 2A _* (A + B).

On tapauksia, joissa polynomia ei voida ottaa huomioon, koska sen termeissä ei ole yhteistä tekijää; Siten nämä algebralliset lausekkeet ovat jaettavissa vain keskenään ja 1. Esimerkiksi: x + y + z.

Algebrallisessa ekspressiossa yleinen tekijä on sen muodostavien termien suurin yhteinen jakaja.

Tekijämenetelmät

On olemassa useita tekijämenetelmiä, joita käytetään tapauksesta riippuen. Jotkut näistä ovat seuraavia:

Yhteinen tekijä

Tässä menetelmässä tunnistetaan nämä yleiset tekijät; eli ne, jotka toistetaan ilmaisun ehdoilla. Sitten jakautuva ominaisuus sovelletaan, suurin yhteinen jakaja poistetaan ja tekijä on valmis.

Toisin sanoen ilmaisun yleinen tekijä tunnistetaan ja jokainen termi on jaettu tämän kesken; Tuloksena olevat termit kerrotaan suurimmalla yhteisella jakajalla tekijän ilmaisemiseksi.

Esimerkki 1

Tekijä (b²x) + (b²ja).

Ratkaisu

Ensimmäinen on kunkin termin yleinen tekijä, joka tässä tapauksessa on B², Ja sitten termit jaetaan yhteisen tekijän välillä seuraavasti:

(b²x) / b² = x

(b²y) / b² = y.

Faktorisointi ilmaistaan, kertomalla yleinen tekijä tuloksena olevilla termeillä:

(b²x) + (b²y) = b² (x + y).

Esimerkki 2

Foektoida (toinen²b -³) + (3ab²-A.

Ratkaisu

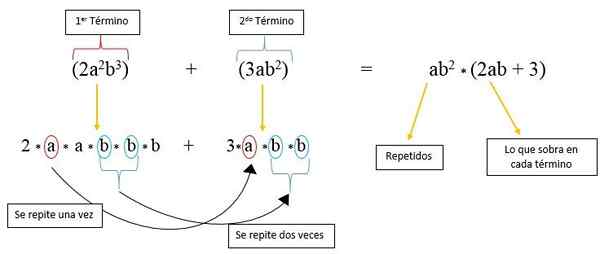
Tässä tapauksessa meillä on kaksi tekijää, jotka toistetaan jokaisella termillä, jotka ovat "A" ja "B" ja jotka nostetaan voimaan. Niiden huomioimiseksi kaksi termiä hajotetaan pitkässä muodossaan:

2_*-lla_*-lla_*b -_*b -_*B + 3A_*b -_*b -

Voidaan nähdä, että “A” -kerroin toistetaan vain kerran toisella termillä ja ”B” -kerroin toistetaan tässä kahdesti; Joten ensimmäisellä aikavälillä on vain 2, tekijä "A" ja yksi "B"; Kun taas toisella toimikaudella vain 3 pysyy.

Siksi se on kirjoitettu niin monta kertaa kuin "A" ja "B" toistetaan ja kerrotaan tekijöillä, jotka on jäljellä jokaisesta termistä, kuten kuvassa havaitaan:

Ryhmittelytekijä

Kuten kaikissa tapauksissa polynomin suurin yhteinen jakaja ilmaistaan ​​selvästi, on tarpeen tehdä muita toimenpiteitä voidakseen kirjoittaa polynomi uudelleen ja siten tekoon.

Voi palvella sinua: Kartiomaiset osat: Tyypit, sovellukset, esimerkit

Yksi näistä vaiheista on ryhmitellä polynomin termit useisiin ryhmiin ja käyttää sitten yhteistä tekijämenetelmää.

Esimerkki 1

Tekijä AC + BC + AD + BD.

Ratkaisu

On 4 tekijää, joissa kaksi ovat yleisiä: ensimmäisellä termillä se on "C" ja toisessa se on "D". Tällä tavalla nämä kaksi termiä on ryhmitelty ja erillinen:

(AC + BC) + (AD + BD).

Nyt on mahdollista soveltaa yleistä tekijämenetelmää, joka jakamalla jokainen termi sen yhteisen tekijän mukaan ja kertomalla sitten yleinen tekijä tuloksena olevilla termeillä, kuten tämä:

(AC + BC) / C = A + B

(ad + bd) / d = a + b

C (A + B) + D (A + B).

Nyt saadaan binomi, joka on yleinen molemmille termeille. Tekijäksi se kerrotaan jäljellä olevilla tekijöillä; Tällä tavalla sinun täytyy:

Ac + bc + ad + bd =  (C + D) _* (A + B).

Tarkastustekijä

Tätä menetelmää käytetään tekijään neliömäisiä polynomeja, joita kutsutaan myös trinomeiksi; eli ne, jotka on rakennettu kirveksi² ± BX + C, missä arvon arvo on erilainen kuin 1. Tätä menetelmää käytetään myös, kun trinomiaalilla on x -muoto² ± BX + C ja "A" = 1 -arvo.

Esimerkki 1

Tekijä X² + 5x + 6.

Ratkaisu

Sinulla on x -muodon neliömäinen trinomiaali² ± BX + C. Ensinnäkin on havaittu kaksi numeroa, että moninkertaistuessa johtaa C -arvoon (ts. 6) ja että sen summa on yhtä suuri kuin B -kertoimet. Nämä numerot ovat 2 ja 3:

2 _* 3 = 6

2 + 3 = 5.

Tällä tavalla ilmaisu yksinkertaistetaan seuraavasti:

(x² + 2x) + (3x + 6)

Jokainen termi on tekijä:

• Varten (x² + 2x) Yleinen termi poistetaan: x (x + 2)
• For (3x + 6) = 3 (x + 2)

Siten lauseke pysyy:

x (x +2) +3 (x +2).

Koska sinulla on yhteinen binomiaalinen, ilmaisun vähentämiseksi, se kertoo tämän jäljellä olevilla ehdoilla ja sen on:

x² + 5x + 6 = (x + 2) _* (x + 3).

Esimerkki 2

Fotoppaa 4a² + 12a +9 = 0.

Ratkaisu

Sinulla on kirvesmuodon neliömäinen trinomi² ± BX + C ja sen tekijä kertoo kaiken ekspression x: n kertoimella²; Tässä tapauksessa 4.

Neljäs² + 12a +9 = 0

Neljäs² (4) + 12a (4) + 9 (4) = 0 (4)

16 a² + 12a (4) + 36 = 0

4² -lla² + 12a (4) + 36 = 0

Nyt on löydettävä kaksi numeroa, että moninkertaistettaessa toistensa kanssa johtaa C: n arvoon (joka on 36) ja että liitettäessä termin "A" kerroin, joka on 6.

6 _* 6 = 36

6 + 6 = 12.

Tällä tavalla ilmaus kirjoitetaan uudelleen ottaen huomioon sen 4² -lla² = 4a _* Neljäs. Siksi jakautuvaa ominaisuutta sovelletaan jokaiseen termiin:

Voi palvella sinua: Mackinder Box

(4a + 6) _* (4a + 6).

Lopuksi lauseke jaetaan a: n kertoimella²; eli 4:

(4a + 6) _* (4a + 6) / 4 = ((4a + 6) / 2) _* ((4a + 6)/ 2).

Ilmaisu on seuraava:

Neljäs² + 12a +9 = (2a +3) _* (2a + 3).

Tekijä merkittävien tuotteiden kanssa

On tapauksia, joissa polynomien täysin ottamiseksi aikaisempien menetelmien kanssa siitä tulee erittäin pitkä prosessi.

Siksi lauseke voidaan kehittää merkittävien tuotteiden kaavoilla ja siten prosessi yksinkertaistaa. Eniten käytettyjä merkittäviä tuotteita ovat:

• Kahden neliön ero: (a² - b -²) = (a - b) _* (A + B)
• Täydellinen summan neliö: a² + 2AB +B² = (A + B)²
• Täydellinen eron neliö: a² - 2AB + B² = (a - b)²
• Kahden kuutio ero: a³ - b -³ = (a-b)_*(² + AB + B²-A
• Kahden kuutiosumma: a³ - b -³ = (A + B) _* (² - AB + B²-A

Esimerkki 1

Tekijä (5² - x²-A

Ratkaisu

Tässä tapauksessa on olemassa kaksi neliötä; Siksi käytetään merkittävän tuotteen kaavaa:

(² - b -²) = (a - b) _* (A + B)

(5² - x²) = (5 - x) _* (5 + x)

Esimerkki 2

Foektoida 16x² + 40x + 25²

Ratkaisu

Tässä tapauksessa summa on täydellinen neliö, koska kaksi neliötermeä voidaan tunnistaa, ja jäljellä oleva termi on seurausta moninkertaistamisesta kaksi ensimmäisen termin neliöjuurella, toisen termin neliöjuurella.

-lla² + 2AB +B² = (A + B)²

Tekijäksi lasketaan vain ensimmäisen ja kolmannen termin neliöjuuret:

√ (16x²) = 4x

√ (25²) = 5.

Sitten kaksi tuloksena olevaa termiä ilmaistaan ​​erotettuna operaation merkinnällä, ja kaikki neliön polynomi on kohonnut:

16x² + 40x + 25² = (4x + 5)².

Esimerkki 3

Foektoida 27A³ - b -³

Ratkaisu

Lauseke edustaa vähennystä, jossa kaksi tekijää kohotetaan kuutioon. Niiden ottamiseksi sovelletaan kuutioeron huomattavan tuotteen kaavaa, mikä on:

-lla³ - b -³ = (a-b)_*(² + AB + B²-A

Siten tekijäksi kuutiojuuri poistetaan kustakin binomin termistä ja kerrotaan ensimmäisen termin neliöllä, plus ensimmäisen termin tuote, ja toinen termi neliömäinen neliö.

27a³ - b -³

³√ (27a³) = 3a

³√ (-b³) = -b

27a³ - b -³ = (3a - b) _* [(3a)² + 3AB + B²)

27a³ - b -³ = (3a - b) _* (9a² + 3AB + B²-A

Tekijä Ruffini -sääntöllä

Tätä menetelmää käytetään, kun sinulla on yli kaksi astetta polynomi, ekspression yksinkertaistamiseksi useille pienemmille polynomeille.

Esimerkki 1

Foctorce q (x) = x⁴ - 9x² + 4x + 12

Ratkaisu

Ensinnäkin 12 12: n jakajia etsitään, mikä on riippumaton termi; Nämä ovat ± 1, ± 2, ± 3, ± 4, ± 6 ja ± 12.

Voi palvella sinua: 2: 2: MIKSI JA SELLITTELY

Sitten X korvataan näillä arvoilla, vähiten suurimpaan, ja niin se määritetään millä arvoilla jako on tarkka; Eli loput on oltava 0:

x = -1

Q (-1) = (-1)⁴ - 9 (-1)² + 4 (-1) + 12 = 0.

x = 1

Q (1) = 1⁴ - 9 (1)² + 4 (1) + 12 = 8 ≠ 0.

x = 2

Q (2) = 2⁴ - 9 (2)² + 4 (2) + 12 = 0.

Ja niin edelleen jokaiselle jakajalle. Tässä tapauksessa löydetyt tekijät ovat x = -1 ja x = 2.

Ruffini -menetelmää sovelletaan nyt, minkä mukaan lausekertoimet jaetaan löydetyillä tekijöillä, jotta jako on tarkka. Polynomitermit järjestetään suuremmasta alempaan eksponenttiin; Jos termi puuttuu sekvenssissä seuraavalla asteella, 0 asetetaan paikoilleen.

Kertoimet sijaitsevat kaaviossa, kuten seuraavassa kuvassa nähdään.

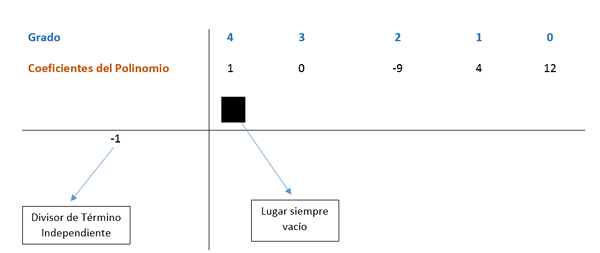
Ensimmäinen kertoimet lasketaan ja kerrotaan jakajilla. Tässä tapauksessa ensimmäinen jakaja on -1, ja tulos sijoitetaan seuraavaan sarakkeeseen. Sitten kertoimen arvo kyseisellä tuloksella lisätään pystysuoraan ja tulos on asetettu alapuolelle. Tällä tavalla prosessi toistetaan viimeiseen sarakkeeseen asti.

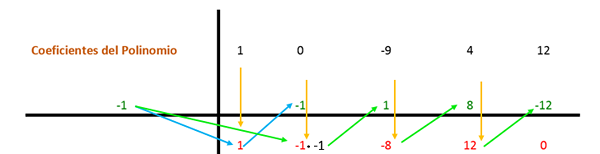
Sitten sama menettely toistetaan uudelleen, mutta toisen jakajan kanssa (joka on 2), koska lauseketta voidaan silti yksinkertaistaa.

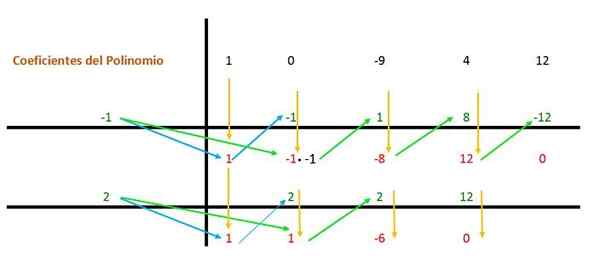
Siten jokaiselle saavutetulle juurelle polynomilla on termi (x - a), missä “A” on juuren arvo:

(x - (-1)) _* (x - 2) = (x + 1) _* (x - 2)

Toisaalta nämä termit tulisi kertoa muualla, jotka pysyivät Ruffini 1: 1 ja -6 -säännöstä, jotka ovat tekijöitä, jotka edustavat astetta. Tällä tavoin ilmaisut muodostaa: (x² + X - 6).

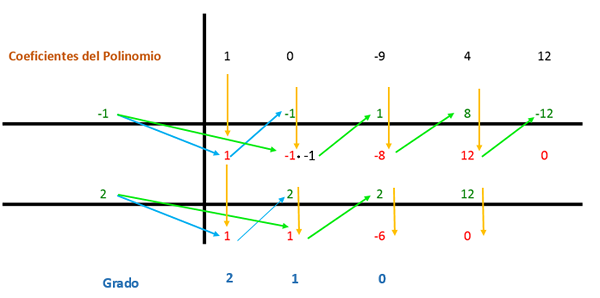
Polynomitekijän tulos Ruffinin menetelmällä on:

x⁴ - 9x² + 4x + 12 = (x + 1) _* (x - 2) _* (x² + X - 6)

Lopuksi, luokan 2 polynomi, joka esiintyy edellisessä lausekkeessa, voidaan kirjoittaa uudelleen (x+3) (x-2). Siksi lopullinen tekijä on:

x⁴ - 9x² + 4x + 12 = (x + 1) _* (x - 2)_*(x+3)_*(X-2).

Viitteet

1. Arthur Goodman, L. H. (1996). Algebra ja trigonometria analyyttisellä geometrialla. Pearson -koulutus.
2. J, V. (2014). Kuinka opettaa lapsille polynomin ottamisesta.
3. Manuel Morillo, a. S. (S.F.-A. Matematiikka sovellusten kanssa.
4. Roelse, P. Lens. (1997). Lineaariset menetelmät polynomitekijälle äärellisissä kentissä: teoria ja toteutukset. University Essen.
5. Sharpe, D. (1987). Renkaat ja tekijä.