Sähkökenttävirta

Mikä on sähkökenttävirta?

Hän sähkökenttävirta tai yksinkertaisesti sähkövirta on skalaarinen määrä, joka on verrannollinen pinnan ylittävien sähkökenttäviivojen lukumäärään. Sitä merkitään pääomakirjepääoma φ (phi).

Sähkökenttä ei oikeastaan ​​"virtaa" vesivirran tapaan, vaikka nesteen virtauslinjat muistuttavat sähkökentän linjoja.

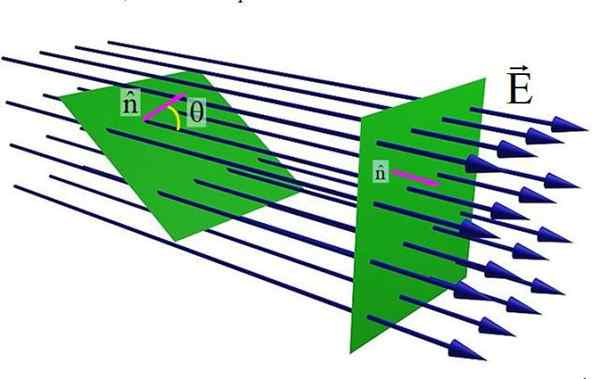
Kuvio 1. Sähkökenttä virtaus tasaisen pinnan läpi. Lähde: Wikimedia Commons.

Yläkuvio näyttää tasaisen pinnan, jonka sähkökenttä on ylittänyt JA. Kun normaali yksikkövektori pintaan n ja kenttä JA Ne ovat yhdensuuntaisia, pinnan ylittävien kenttäviivojen määrä on maksimiarvo. Mutta kun kulma θ kasvaa n ja JA, Vihreän pinnan läpi kulkevien linjojen lukumäärä on alempi.

Toisaalta sähkökenttävirta riippuu myös JA, Koska mitä korkeampi tämä, sitä enemmän kenttäviivoja ne ylittävät pinnan. Ja tietysti, mitä suurempi mainitun pinnan pinta -ala on myös virtaus, joten seuraava yhtälö on perustettu:

Φ = e ∙ sosθ

Tämä lauseke on yhdenmukainen skalaarituotteen kanssa vektorien keskuudessa JA ja n-

Φ = (JA Olla nS

Yksikkö sähkökenttävirtalle kansainvälisessä yksikköjärjestelmässä, jos n on.m²/C (Newton X Square Metro/Coulomb). Vaihtoehtoisesti, koska kenttä on myös mitattu V/M (voltti metrolla), sähkövirta on (v ∙ m) m).

Esimerkit

Määritelmän mukaan sähkövirta voi olla positiivinen, negatiivinen tai yhtä suuri kuin 0. Sähkökentän virtaus on:

Se voi palvella sinua: magnetointi: kiertoradan ja spin -magneettinen momentti, esimerkkejä

-Positiivinen, kun kulma θ välillä JA ja n Se on alle 90º, koska cos θ on suurempi kuin nolla.

-Negatiivinen, jos tämä kulma on suurempi kuin 90º, koska silloin cos θ on pienempi kuin nolla.

-Tyhjä, kun θ on arvoinen tarkalleen 90º, koska cos 90º = 0 ja kenttäviivat tässä tapauksessa ovat tangentiaalisia pintaan.

-Toisaalta, jos kulma JA ja n Se on yhtä suuri kuin 0, virtaus saa suurimman arvon.

Nämä mahdollisuudet esitetään seuraavassa kuvassa:

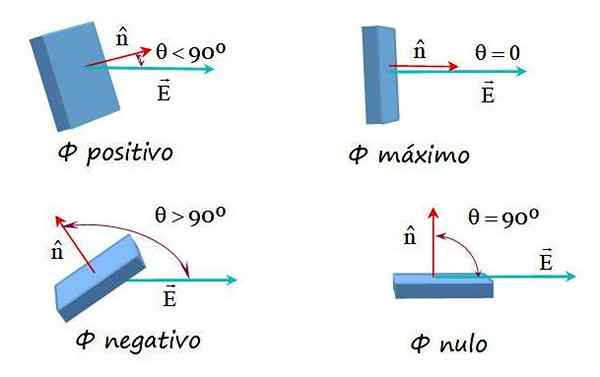Kuva 2. Esimerkkejä sähkökentän virtauksesta, jolla on erilaisia ​​suuntauksia kentän ja normaalin pintavektorin välillä. Lähde: f. Zapata.

Sähkökenttävirta mielivaltaisella pinnalla

Aikaisemmin sähkökenttävirta määritettiin tietyssä tapauksessa tasainen kenttä, joka vaikutti tasaiseen pintaan. Mielivaltaiselle pinnalle ja/tai ei -epäyhtenäiselle sähkökentälle kulma JA ja n voi vaihdella pisteestä toiseen.

Seuraavassa kuvassa on kaksi esimerkkiä, vasemmalle kaareva pinta ja oikealla puolella suljettu pinta.

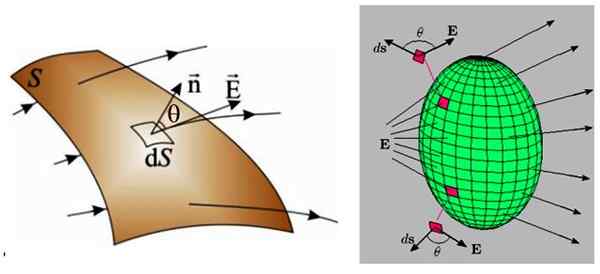Kuva 3. Vasemmalla mielivaltainen pinta, jonka läpi ei -yhtenäinen sähkökenttäristit. Oikealla ei -epäyhtenäinen sähkökenttä ylittää suljetun pinnan, joten nettovirta on siis mitätön. Lähde: f. Zapata.

Molemmissa tapauksissa pinta on jaettu paljon pienempiin alueisiin, jotka ovat äärettömiä pienikokoisia, nimeltään DS, jolle se myös ylittää äärettömän pienen virtauksen Dφ:

dφ = (JAOllan) Ds = (ecosθ) ds

Kokonaiskenttä saadaan lisäämällä kaikki nämä äärettömät maksut:

S -symboli integraalin alaindeksi osoittaa, että se on laskettava koko pinnalla. Jos tämä on suljettu, se on merkitty pienellä ympyrällä integraalilla:

Voi palvella sinua: Antoine -vakiot: kaavat, yhtälöt, esimerkit

Suljettujen pintojen tapauksessa, n Aina osoita, joten virtauksella on merkki +, kun se on lähtevä, koska kulma JA ja n on alle 90º ja merkki - kun kenttä on saapuva, ​​koska silloin kulma JA ja n on yli 90º (katso kuva 2).

Huomaa, että oikealla olevalla suljetulla pinnalla pinnalle tulevien kenttäviivojen lukumäärä on yhtä suuri kuin ulos tulevien linjojen lukumäärä. Siksi nettovirta, joka on määritelty tulevan virtauksen ja lähtevän virtauksen algebrallisena summana, on mitätön.

Sähkökenttälähde on tässä tapauksessa pinnan ulkopuolella, mutta nettovirta erottaisi 0: sta, jos sähkökenttälähde (kuormitusten jakautuminen) olisi pinnan sisällä.

Harjoitukset

Harjoitus 1

Sinulla on sähkökenttä JA = 3.5 kN/c x ja tasainen suorakaiteen muotoinen pinta 0.35 m leveä 0.7 m pitkä. Etsi sähkökenttävirta, joka ylittää suorakulmion seuraavissa tapauksissa:

a) pinta on yhdensuuntainen tason yz.

b) Suorakulmio on yhdensuuntainen XY -tason kanssa.

c) Normaali taso muodostaa 40º kulman X -akselin kanssa ja sisältää akselin ja.

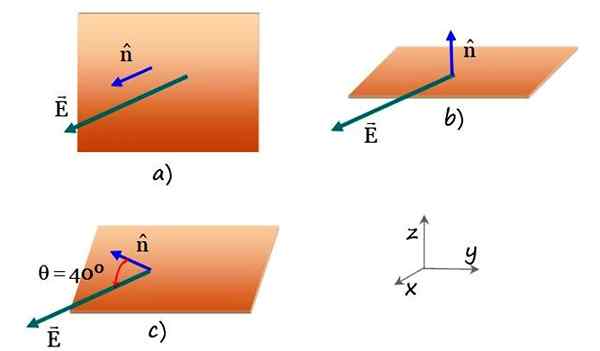Kuva 4. Suorakulmainen taso, joka on ylitetty tasaisella sähkökentällä eri tason suunnissa. Lähde: f. Zapata.

Liittää jhk

Normaali vektori ja sähkökenttävektori ovat yhdensuuntaiset, joten kahden välinen kulma θ on 0º ja sähkövirtaus on:

Φ = (e ∙ s) cos 0 = e ∙ s

Suorakulmion alue on:

Voi palvella sinua: Parallegrammimenetelmä: Esimerkkejä, ratkaisut harjoitukset

S = 0.35 m x 0.7 m = 0.245 m²

Korvaaminen φ:

Φ = e ∙ s = 3.5 x 10³ N/c × 0.245 m² = 857.5 n ∙ m² /C.

Ratkaisu b

Sähkökentän virtaus on 0, koska vektorit JA ja n Ne ovat kohtisuorassa toisiaan kohtaan.

Liuos C

Kulma θ kentän välillä JA ja normaali vektori n on 40º (katso kuva), siksi:

Φ = e ∙ s ∙ cos θ = 3.5 x 10³ N/c × 0.245 m² × COS 40º = 656.9 n ∙ m² /C.

Harjoitus 2

Laske sähkökenttävirta, joka tuottaa positiivisen täsmällisen kuorman, joka_jompikumpi = 2 μC, joka sijaitsee sädepallon keskellä r = 5 cm.

Ratkaisu

Kuorman q tuottama kenttä_jompikumpi Se ei ole yhtenäistä, mutta Coulombin laista tiedetään, että pallon pinnalla sillä on suuruus:

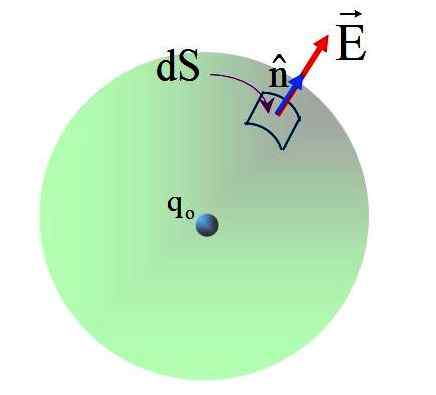Kuva 5. Pallon pinnalla tuotettujen kentän kärpäset täsmällisellä kuormalla sen keskellä. Lähde: f. Zapata.

Kentällä on säteittäinen suunta ja normaali vektori n, Siksi kahden vektorin välinen kulma on 0 pallomaisen pinnan kaikissa pisteissä. Korvaus:

Sinun täytyy:

DS: n integraali koko pallomaisella pinnalla on sen pinta -ala, joka on 4πr^2, siksi:

Joka päättelee, että sähkökenttävirta ei riipu pinnasta, vaan siihen lukittuun kuormaan.

Sen arvo on:

Φ = 4π × 9 × 10⁹ x 2 × 10^-6 N⋅m²/C = 2.3 x 10⁵ N⋅m²/C

Viitteet

1. Bauer, W. 2011. Fysiikka tekniikkaan ja tieteisiin. Osa 1. MC Graw Hill.
2. Figueroa, D. (2005). Sarja: Tieteen ja tekniikan fysiikka. Nide 5. Sähköstaatiikka. Toimittanut Douglas Figueroa (USB).
3. Giambattista, a. 2010. Fysiikka. Toinen. Ed. McGraw Hill.
4. Giancoli, D.  2006. Fysiikka: sovellusten periaatteet. Kuudes. Ed Prentice Hall.
5. Sears, Zemansky. 2016. Yliopiston fysiikka, jolla on moderni fysiikka. 14. päivä. Ed. Osa 1. Pearson.