Staattinen kitkakerroin, esimerkki, liikunta

Se staattinen kitka Kahden pinnan välillä syntyy voima, kun toinen pinta ei liu'uta toiseen. Sillä on suuri merkitys, koska se antaa meille mahdollisuuden edetä kävellessä, koska se on nykyinen voima lattian ja kengän pohjan välillä. 

Se on myös staattinen kitka, joka näkyy jalkakäytävän ja auton renkaiden välillä. Jos tätä voimaa ei ole läsnä, auton on mahdotonta alkaa liikkua, kuten autossa, joka yrittää aloittaa jäisellä pinnalla: Pyörät liukuvat, mutta auto ei etene.

Kuvio 1. Esimerkki kitkavoimasta

Staattinen kitka riippuu kosketuksessa olevien pintojen karheudesta ja myös valmistetun materiaalin tyypistä. Siksi renkaat ja urheilukengät ovat kumia kitkan lisäämiseksi jalkakäytävällä.

Staattisessa kitkamallissa materiaalien ominaisuudet ja pintojen välinen karheusaste on yhteenveto nimeltään lukumäärä staattinen kitkakerroin, joka määritetään kokeellisesti.

[TOC]

Staattinen kitkakerroin

Kuva 2. Kaltetun taulukon kirja pysyy levossa kirjan ja taulukon välisen staattisen kitkavoiman takia. Lähde: f. Zapata.

Yläkuvio näyttää kirjan, joka on levossa pöydällä, jolla on 15,7º: n kallistus.

Jos kirjan pinnat ja pöytä olisivat erittäin sileitä ja kiillotettuja, kirjaa ei voitu pitää levossa. Mutta koska ne eivät ole, ilmestyy voima, joka on tangentti kosketuksessa oleville pinnoille, nimeltään Force of staattinen kitka. 

Jos kallistuskulma oli riittävän suuri, niin ei ole tarpeeksi staattinen kitka Kirjan tasapainottaminen ja tämä alkaa liukua.

Tässä tapauksessa kirjan ja pöydän välillä on myös kitka, mutta se olisi a joukko Dynaaminen kitka, kutsutaan myös kineettinen kitka.

Staattisen kitkan ja dynaamisen kitkan välillä on raja, joka tapahtuu sillä hetkellä, jolloin staattinen kitka saavuttaa maksimiarvonsa.

Voi palvella sinua: Doppler -vaikutus: Kuvaus, kaavat, tapaukset, esimerkit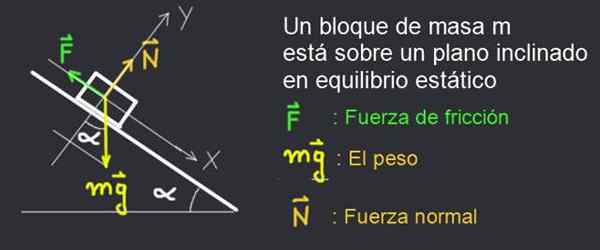Kuva 3. Kaltevan tason lepolohko on levossa staattisen kitkavoiman ansiosta. Lähde: f. Zapata.

Tarkastellaan kuviossa 2 massa -M -kirjan voimakaaviota, joka pysyy levossa α -kallistustasolla.

Kirja pysyy levossa, koska kitkavoima F, staattinen tyyppi, tasapainottaa järjestelmää.

Jos kaltevuuskulma kasvaa hiukan, niin kosketuspintojen on annettava enemmän kitkavoimaa, mutta staattisen rubbin määrä_Max, tarkoittaen:

F ≤ f_Max.

Suurin staattinen kitkavoima riippuu kosketuksessa olevien pintojen materiaaleista ja karheuden asteesta sekä otteen lujuudesta.

Staattinen kitkakerroin μ_ja Se on positiivinen luku, joka riippuu kosketuksessa olevien pintojen ominaisuuksista. Normaali voima N että lohkoon kohdistuva taso vastaa lohkon pinnan ja tason välillä. Siten ne määrittävät pintojen tarjoaman maksimaalisen kitkavoiman, kun maanvyörymiä ei ole:

F_Max = μ_ja N

Lyhyesti sanottuna, staattinen kitkavoima seuraa seuraavaa mallia:

F ≤ μ_ja N

Esimerkki: Staattisen kitkakertoimen määrittäminen

Staattinen hankauskerroin on mitoiton luku, joka määritetään kokeellisesti jokaiselle pintaparille. 

Tarkastellaan lohkoa muualla kuvassa 2. Seuraavat joukot toimivat siihen:

- Kitkavoima: F

- Massalohkon M painog

- Normaali voima: N

Koska lohko on levossa eikä sillä ole kiihtyvyyttä, Newtonin toisen lain mukaan tuloksena oleva voima -vektorisumma -on mitätön:

F + N + mg = 0 -

Sitä pidetään kiinteänä XY -koordinaattijärjestelmänä X -akselin kanssa kaltevaa tasoa ja akselia pitkin ja kohtisuorassa siihen, kuten kuvassa 2 esitetään.

Se voi palvella sinua: Kuule voima: pinta- ja massavoimat

Voimat on erotettava Cartesian komponenttiensa mukaan, mikä johtaa seuraaviin yhtälöjärjestelmiin:

-Komponentti x: -F + mg sen (α) = 0

-Komponentti ja: N - mg cos (α) = 0

Ensimmäisestä yhtälöstä staattisen kitkan arvo puhdistetaan:

F = mg sen (α)

Ja toisesta normaalin voiman arvo:

N = mg cos (α)

Staattinen kitkavoima johtuu seuraavasta mallista:

F ≤ μ_ja N

Korvataan eriarvoisuudessa aiemmin saatuja arvoja, joita meillä on:

Mg Sen (α) ≤ μ_ja mg cos (α)

Otetaan huomioon, että α -arvojen välillä välillä 0º - 90º, sini- ja kosiinifunktiot ovat molemmat positiivisia ja että rinnan ja kosinin välinen osoitus on tangentti, olemme lähteneet:

Tan (α) ≤ μ_ja

Tasa -arvo täyttyy tietylle α -arvolle, jota kutsutaan kriittiseksi kulmaksi ja että merkitsemme α*: lle, ts

μ_ja = Tan (α*)

Kriittinen kulma määritetään kokeellisesti, lisäämällä vähitellen kallistumista oikeaan kulmaan, jossa lohko alkaa liukua, eli kriittinen kulma α*.

Kuvion 1 kirjassa tämä kulma määritettiin kokeellisesti, mikä johtaa 24º. Sitten staattinen kitkakerroin on:

μ_ja = Tan (24º) = 0,45.

Se on positiivinen luku välillä 0 ja ääretön. Kyllä μ_ja = 0 pintaa ovat täysin sileät. Kyllä μ_ja → ∞ Pinnat ovat täydellisesti kytkettyjä tai hitsattuja.

Yleensä kitkakertoimen arvo on välillä 0–10.

Harjoittele

Pique -kisoissa tai dragstersissa saavutetaan jopa 4G: n kiihtyvyydet, jotka saavutetaan juuri silloin, kun renkaat eivät liu'uta jalkakäytävän suhteen.

Tämä johtuu siitä, että staattinen kitkakerroin on aina suurempi kuin dynaaminen kitkakerroin.

Olettaen, että ajoneuvon ja kuljettajan kokonaispaino on 600 kg ja että takapyörät tukevat 80% painosta, määritä staattinen kitkavoima 4G -aloituksen aikana ja renkaiden ja päällysteen välinen staattinen kitkakerroin ja päällyste.

Voi palvella sinua: Orion Nebula: Alkuperä, sijainti, ominaisuudet ja tiedotKuva 4. "Dragster" aloitushetkellä. Lähde: Pixabay.

Ratkaisu

Newtonin toisen lain mukaan tuloksena oleva voima on yhtä suuri kuin ajoneuvon kokonaismassa, joka johtuu sen hankkimasta kiihdytyksestä.

Koska ajoneuvo on pystysuorassa tasapainossa, normaali ja paino on kumottu jäljellä johtuvana kitkan voimana F, jota jalkakäytävä käyttää vetopyörien kosketusalueelle, jäljellä olevaa:

F = M (4G) = 600 kg (4 x 9,8 m/s²) = 23520 N = 2400 kg-F

Toisin sanoen vetovoima on 2,4 tonnia.

Pyörän käyttämä kitkavoima lattialle palaa takaisin, mutta sen reaktio, joka on sama ja vastakkainen, toimii renkaaseen ja menee eteenpäin. Se on voima, joka ajaa ajoneuvoa.

Tietysti moottori tuottaa kaiken tämän voiman, että pyörän läpi yritetään työntää lattiaa taaksepäin, mutta pyörä ja lattia kytketään kitkavoimalla. 

Staattisen kitkakertoimen määrittämiseksi käytämme sitä tosiasiaa, että saatu F on suurin mahdollinen kitka, koska olemme suurimmalla kiihtyvyysrajalla, siksi:

F = μ_ja N = μe (0,8 mg)

Se tosiasia, että vedon takapyörät tukevat 0,8 kertaa painoarvoa. Kitkakertoimen puhdistaminen saadaan:

μ_ja = F / (0,8 mg) = 23520 N / (0,8 x 600 kg x 9,8 m / s^2) = 5.

Johtopäätös: μ_ja = 5.

Viitteet

1. Alonso m., Suomalainen. 1970. Fysiikan osa I: Mekaniikka. Inter -American Educational Fund S.-Lla.
2. Bauer, W. 2011. Fysiikka tekniikkaan ja tieteisiin. Osa 1. MC Graw Hill.
3. Hewitt, s. 2012. Käsitteellinen fysiikka. Viides painos.
4. Rex, a. 2011. Fysiikan perusteet. Pearson. 190-200.
5. Nuori, Hugh. 2015. Yliopiston fysiikka, jolla on moderni fysiikka. 14. ed. Pearson.