Mitkä ovat kolmionmuodot? Ominaisuudet ja mielenosoitukset

Se tunnetaan nimellä kolmiomaiset numerot lukumäärän sekvenssiin, jotka saadaan tekemällä tasasivuisen kolmion pisteiden järjestely tai luku. Ensimmäiset sekvenssit ovat: 1, 3, 6, 10, 15, 21, ..

Ensimmäinen kolmion muotoinen ongelma on 1, toinen on 3, koska se saadaan lisäämällä kahden pisteen rivi edelliseen, muodostaen tasaisen kolmion kolmen elementin kanssa.

Kuvio 1. Kuuden ensimmäisen kolmion lukumäärän sekvenssi. Lähde: Wikimedia Commons. Melchoir/CC BY-SA (https: // creativecommons.Org/lisenssit/by-SA/3.0)

Kolmas on 6, joka ilmestyy lisäämällä kolmen pisteen rivin edelliseen järjestelyyn, niin että kolmen pisteen kolmio muodostuu sivua kohti. Sekvenssin 10 saadaan lisäämällä uusi rivi edelliseen järjestelyyn siten, että neljän pisteen kolmio muodostuu sivua kohti.

Kaava, jonka avulla voit löytää elementin n Kolmion muotoisesta sekvenssistä tunnustaa, että kolmionmuotoinen etuosa on:

T_n = T_N-1 + n

Kuuden ensimmäisen kolmion lukumäärän luettelo saavutetaan näin:

-Ensimmäinen: 1

-Toinen: 1 + 2 = 3

-Kolmas: (1 +2) + 3 = 3 + 3 = 6

-Huone: (1 + 2 + 3) + 4 = 6 + 4 = 10

-Viides: (1 + 2 + 3 + 4) + 5 = 10 + 5 = 15

-Kuudes: (1 + 2 + 3 + 4 + 5) + 6 = 15 + 6 = 21

[TOC]

Kolmionlukujen ominaisuudet

1.- Kolmionlukujen sekvenssin N-Simo TN-kolmion lukumäärä on puolet n: stä kerrottuna n+1: n:

T_n = ½ n (n+1)

2.- Kolmioluvun N-ésimon summa, jolla on etuosan kolmion lukumäärä, toisin sanoen (n-1) -sheimo, se on neliömäinen:

T_n + T_N-1= n²

3.- Ero kolmion lukumäärässä n-tämä vähemmän kolmion muotoinen n-ésimo vähemmän on n:

T_n - T_N-1 = n

4.- Ensimmäisten kolmionmuotoisten lukujen summaa kutsutaan tetraedrinumeroksi SN ja se on yhtä suuri kuin tuotteen kuudes osa kerrottuna (n + 1) ja kerrottuna (n + 2):

Voi palvella sinua: verotus

S_n= ⅙ n (n + 1) (n + 2)

5.- Jokainen luonnollinen luku N on seurausta kolmen kolmion luvun summasta:

N = Δ1 + Δ1 + Δ3

Suuri matemaatikko Carl Friedrich Gauss löysi tämän viimeisen kiinteistön tai lauseen vuonna 1796, jonka hän teki päiväkirjaansa asettamalla Kreikan ihailun Eureka! mitä se tarkoittaa "Olen saavuttanut sen".

Se oli sama sana, jota kreikkalaiset arkkitehdit käyttivät paljon aikaisemmin, kun hän määritteli upotetun ruumiin näennäisen painon.

Tässä suhteessa nolla -lukumäärä pidetään kolmionmuotoisena ja toistoa voi olla.

Esittelyt

- Esittely 1

Todista, että kolmionumero n-Tämä on:

T_n = ½ n (n+1)

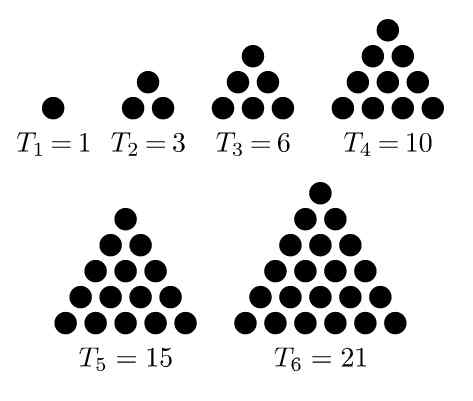
Edellinen kaava on helppo päätellä, jos ymmärrämme, että voimme lisätä saman määrän pisteitä kolmion muotoiseen järjestelyyn pisteiden nelikulmion muodostamiseksi.

Koska järjestelypisteiden kokonaismäärä kvadrilateraalisesti on rivien lukumäärä n kerrottuna sarakkeiden lukumäärällä (N+1), Sitten kolmionmuotoisessa järjestelyssä on vain puolet järjestelyn pisteistä nelinkertaisen muodossa.

Tässä on esitetty kuvassa 2.

Kuva 2. Neliömäinen järjestely, jossa pisteiden kokonaismäärä on rivien lukumäärä n kerrottuna sarakkeiden lukumäärällä N+1. Pisteiden kokonaismäärä on myös kahdesti kolmion muotoinen järjestely. Lähde: Wikimedia Commons.

- Esittely 2

Osoittaa, että summa n-Tämä kolmionumero n-Vähemmän yksi Kolmion lukumäärä on n Neliö:

T_n + T_N-1= n²

On jo osoitettu, että kolmion lukumäärä n-Tämän annetaan:

T_n= ½ n (n+1)

Siksi etuosan kolmion lukumäärä on:

T_N-1 = ½ (n-1) ((n-1) + 1) = ½ n (n-1)

Molempien jäännösten summa:

T_n + T_N-1 = ½ n (n + 1) + ½ n (n - 1)

½ N saadaan:

T_n + T_N-1 = ½ n [(n + 1) + (n - 1) = ½ n [n + 1 + n - 1]

Ja heti lauseke yksinkertaistetaan kiinnikkeen sisällä:

Se voi palvella sinua: arviointia välein

T_n + T_N-1 = ½ n [2 n] = ½ 2 n ⋅ n

Muista nyt, että ½ 2: lle on 1 ja että n n on n neliö, sinulla on:

T_n + T_N-1 = n²

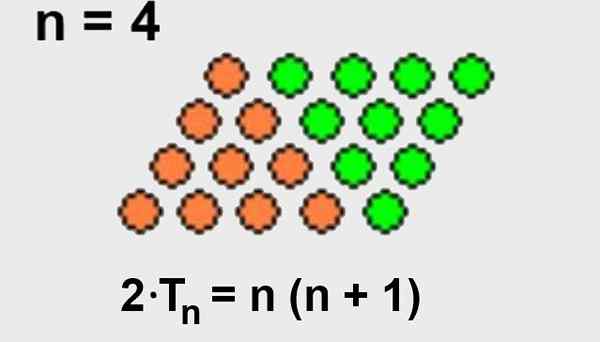
Tämä ominaisuus voidaan myös osoittaa geometrisesti, kolmio valmistuu yksinkertaisesti neliön muodostamiseksi, kuten kuvassa 3 esitetään.

Kuva 3. N-ésimo-kolmion luvun summa etuosan kolmion lukumäärällä on yhtä suuri kuin n neliö. Lähde: Wikimedia Commons.

- Esittely 3

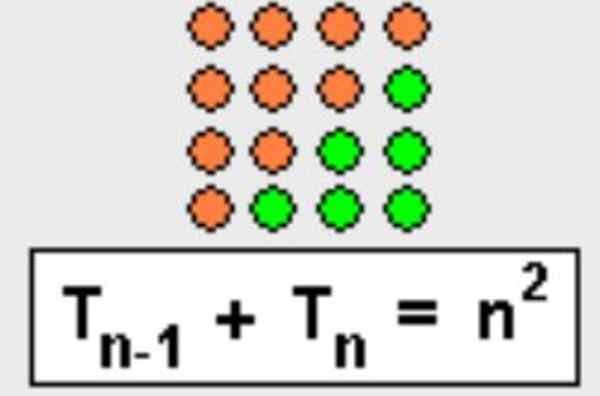
Ero kolmion määrässä järjestysten lukumäärässä n miinus kolmen tilauksen lukumäärä N-1 on n:

T_n - T_N-1 = n

Tämä voidaan testata yksinkertaisesti muistamalla, että seuraavasta kolmionmuotoinen lukumäärä saadaan edellisestä kaavan kautta:

T_n = T_N-1 + n

Ja sieltä on selvää, että T_n - T_N-1 = n. Se on myös helppo visualisoida graafisesti, kuten kuvassa 4 esitetään.

Kuva 4. Kolmion lukumäärän n ero N: n etuosan N-1: n etuosan kolmion muotoinen on n. Lähde: Wikimedia Commons.

- Esittely 5

Ensimmäisten kolmion muotoisten N -numeroiden summa Sn Se on yhtä suuri kuin tuotteen kuudes osa kerrottuna (n + 1) ja kerrottuna (n + 2):

S_n = ⅙ n (n + 1) (n + 2)

Käytämme kolmion määrää järjestystä n: T_n= ½ n (n+1). Ensimmäisen summa n Kolmionluvut merkitsevät sitä S_n  

Esimerkiksi, S₁ tarkoittaa ensimmäisen kolmionmuotoisen kysymyksen summaa, joka epäilemättä on 1.

Katsotaanpa sitten, onko kokeilemamme kaava noudattaa n = 1:

S₁ = ⅙ 1⋅2⋅3 = 1

Itse asiassa kaava n = 1 tarkistetaan. On helppo visualisoida, että N+1: n ensimmäisten kolmionlukujen summa on ensimmäisen n seuraavan kolmionmuodon summa:

S_N+1 = S_n + T_N+1

Oletetaan nyt S_n Se täyttyy N: lle, sitten korvaamme sen edellisessä lausekkeessa ja lisäämme kolminkertaisen järjestyksen lukumäärän N+1-

S_N+1 = [⅙ n (n + 1) (n + 2)] + [½ (n + 1) (n + 2)]]]]]

Voi palvella sinua: Kohtisuorassa linja: Ominaisuudet, esimerkit, harjoitukset

Katsotaanpa askel askeleelta, mitä saadaan:

-Suoritamme kahden murto -lausekkeen summan:

S_N+1 = [2 n (n + 1) (n + 2) + 6 (n + 1) (n + 2)] /12 

-Se poistetaan yleisesti 2 (n + 1) (n + 2) ja yksinkertaistaa: yksinkertaistaa:

S_N+1 = 2 (n + 1) (n + 2) [n +3] / 12 = (n + 1) (n + 2) (n +3) / 6

Aikaisempi tulos on samaa mieltä S -kaavan kanssan Jos N+1 korvataan, mikä on osoitettu induktiolla ensimmäisen kolmion muotoisten termien summan kaava.

Tetraedrinumero

Saatu tulos kutsutaan Tetrahedrinen määräysn määrä n, Koska se on kuin kertyneet kolmionmuotoiset kerrokset, jotka muodostavat tetraedron, kuten seuraavassa animaatiossa esitetään.

Kuva 5. N: n kolmion lukumäärä vastaa N, N-1, ..., 1 kolmiota, jotka muodostavat säännöllisen tetraedron kerrosten pinoa. Lähde: Wikimedia Commons.

Viitteet

1. Camacho J. Kolmionlukujen epäilyttämätön ulkonäkö. Toipunut: Masscience.com
2. Claudio. Kolmiomaiset numerot. Palautettu: yksinkertaisesti numerot. Blogin. com
3. Wikipedia. Kolmionmuotoinen lukumäärä. Palautettu: on.Wikipedia.com
4. Wikipedia. Kolmionmuotoinen lukumäärä. Haettu: vuonna.Wikipedia.com
5. Wikipedia. Numero tretrahedraali. Haettu: vuonna.Wikipedia.com