Pinta- ja massavoimat leikkausvoima

Se Kuulla voimaa Se on yhdistelmävoima, jolle on ominaista, että se on yhdensuuntainen pinnan kanssa, joka on käytetty ja jolla on taipumus jakaa vartalo, siirtymällä toistensa kanssa leikkauksesta johtuvat leikkeet.

Kaaviomaisesti se on esitetty kuvassa 1, joka näyttää puisen lyijykynän kahteen eri kohtaan kohdistetun leikkausvoiman. Leikkausvoima puolestaan ​​vaatii kaksi yhdensuuntaista ja vastakkaista voimaa, jotka niiden voimakkuudesta riippuen kykenevät muodostumaan lyijykynästä tai ehdottomasti murtamaan sen.

Kuvio 1. Käytetty leikkausvoima käsillä aiheuttaa lyijykynän hajoamisen. Lähde: Pixabay.

Joten vaikka puhuisit yksittäisestä kuulevista voimista, he todella soveltavat kaksi voimat, koska leikkausvoima on a yhdistelmävoima. Nämä voimat koostuvat kahdesta voimasta (tai useammasta monimutkaisissa tapauksissa), joita käytetään esineen eri kohdissa.

Kaksi samaa suuruutta ja vastakkaista suuntaa, mutta rinnakkaisilla toimintaviivoilla muodostavat a joukkojoukot. Parit eivät tarjoa käännöstä esineisiin, koska niiden tulos on tyhjä, mutta ne tarjoavat nettomomentin.

Parin kanssa ajoneuvon ohjauspyörän, kuten ajoneuvon ohjauspyörä.

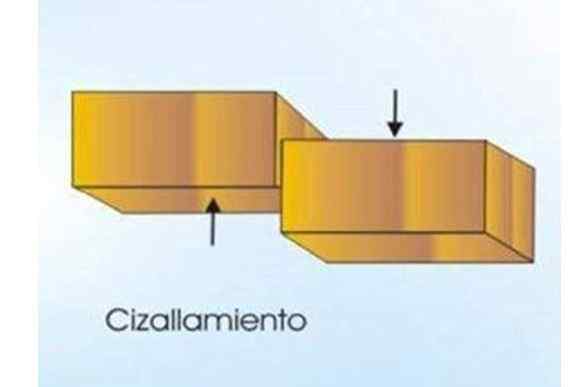Kuva 2. Leikkausvoima jakaa puisen palkin kahteen osaan. Huomaa, että voimat ovat tangentiaalisia Maderon poikkileikkaukselle. Lähde: f. Zapata.

[TOC]

Pintavoimat ja massavoimat

Yhdistetyt voimat ovat osa puheluita pintavoimat, Juuri siksi, että niitä sovelletaan rungon pintaan eivätkä ole millään tavalla sukulaisia ​​massaan. Selventääksesi pistettä, verrataan näitä kahta voimaa, jotka toimivat usein esineisiin: paino- ja kitkavoima.

Se voi palvella sinua: Graff Van Generaattori: Juhlat, miten se toimii, sovellukset

Painon suuruus on p = mg ja koska se riippuu kehon rungosta, se ei ole pintavoima. Se on a Massavoima, Ja paino on ominaisten esimerkki.

Kitka riippuu kuitenkin kosketuspintojen luonteesta eikä sen kehon massasta, jolla se toimii, siksi se on hyvä esimerkki usein esiintyvien ulkonäön pinnallisista voimista.

Yksinkertaiset voimat ja komposiittivoimat

Pinnalliset voimat voivat olla yksinkertainen jompikumpi yhdisteet. Olemme jo nähneet esimerkin leikkausvoimassa koostuvasta voimasta, ja toisaalta kitka on esitetty yksinkertaisena voimaksi, koska yksi nuoli riittää edustamaan sitä esineestä eristetyssä kehon kaaviossa.

Yksinkertaiset voimat ovat vastuussa kehon liikkumisen muutosten tulostamisesta, esimerkiksi tiedämme, että liikkuvassa esineen ja sen liikkuvan pinnan välinen kineettinen kitkavoima johtaa nopeuden vähentämiseen.

Päinvastoin, komposiittivoimat yleensä muodostuvat rungot ja leikkaus- tai leikkurien tapauksessa lopputulos voi olla leikkaus. Muut pintavoimat, kuten jännitys tai puristus, pidentävät tai puristavat sellaista vartaloa, johon ne toimivat.

Joka kerta, kun tomaatti leikataan kastikkeen tai saksien valmistelemiseksi, käytetään paperiarkkia, kuvatut periaatteet sovelletaan. Leikkaustyökaluilla on yleensä kaksi terävää metallilevyä leikkausvoiman levittämiseksi objektin poikkileikkaukseen.

Voi palvella sinua: mikä on magneettinen hetki? Kuva 3. Leikkausvoima toiminnassa: Veitsenlehti kohdistaa yhden voimista, toinen on normaali, jonka leikkauspöytä kohdistaa. Lähde: Katemangostar - Freepik.On

Kuulla stressiä

Leikkausvoiman vaikutukset riippuvat voiman suuruudesta ja alueesta, jolla se toimii, joten käsitteen suunnittelussa Kuulla stressiä, joka ottaa huomioon sekä voiman että alueen.

Tällä pyrkimyksellä on muita merkityksiä, kuten leikkauslujuus o Leikkaus ja siviilirakenteissa se on erittäin tärkeää.

Sen hyödyllisyys ymmärretään välittömästi tarkasteltaessa seuraavaa tilannetta: Oletetaan, että samassa materiaalissa on kaksi baaria, mutta erilainen paksuus, joihin kohdistuu voimia, kunnes ne rikkovat ne.

On selvää, että paksimman palkin katkaisemiseksi sinun on käytettävä suurempaa voimaa, mutta ponnistus on sama jokaiselle palkille, jolla on sama koostumus. Tämänkaltaiset esseet ovat usein tekniikassa, kun otetaan huomioon asianmukaisen materiaalin valinta ennustetulle rakenteelle.

Ponnistus ja muodonmuutos

Matemaattisesti, jos merkitset leikkauspyrkimyksiä τ, F: n voimakkuuden suuruuteen ja sen alueena, jolla se toimii A, sinulla on keskimääräinen leikkauspyrkimys:

τ_keskiverto= F /a

Koska kansainvälinen järjestelmä on voima ja alueen välinen osuus, on Newton/M², kutsutaan Pascaliksi ja lyhennettynä PA: ksi. Englanninkielisessä järjestelmässä käytetään puntanerä/jalka ² ja punta-voima /tuuma².

Voi palvella sinua: Ratkaisu Heat: Kuinka se lasketaan, sovellukset ja harjoitukset

Monissa tapauksissa leikkauspyrkimyksen kohde on kuitenkin epämuodostumat ja palauttaa sitten alkuperäisen muodonsa rikkomatta, kun ponnistus on lopettanut toiminnan. Oletetaan, että muodonmuutos koostuu pituuden muutoksesta.

Tässä tapauksessa ponnistus ja muodonmuutos ovat verrannollinen, joten seuraavia voidaan nostaa:

Leikkauslujuus ∝ yhtenäisen muodonmuutoksen

Symboli ∝ Se tarkoittaa "verrannollista" ja yhtenäisen muodonmuutoksen suhteen se määritellään pituuden muutoksen väliseksi suhteeksi, jota kutsutaan ΔL: ksi ja alkuperäiseksi pituudeksi, nimeltään L_jompikumpi. Tällä tavalla:

τ ∝ (ΔL / l_jompikumpi-A

Leikkausmoduuli

Yhtenäisellä muodonmuutoksella ei ole yksikköä suhde kahden pituuden välillä. Soittaminen G: lle mainitulle vakiolle:

τ = G (δL / l_jompikumpi-A

G kutsutaan Kuule moduuli o Leikkausmoduuli. Sillä on PassionFly -yksiköitä kansainvälisessä järjestelmässä ja sen arvo riippuu materiaalin luonteesta. Tällaiset arvot on mahdollista määrittää laboratoriossa, harjoittamalla eri voimien vaikutusta monimuotoisiin koostumusnäytteisiin.

Kun edellisen yhtälön leikkausvoiman suuruus on määritettävä, se riittää korvaamaan ponnistelujen määritelmä:

τ = F /a = g (δL / l_jompikumpi-A

Ja selkeä:

F = a × g (δL / l_jompikumpi-A

Leikkausvoimat ovat hyvin usein ja niiden vaikutukset on otettava huomioon lukuisissa tieteen ja tekniikan näkökohdissa. Rakennuksissa ne esiintyvät palkkien tukipisteissä, ne voivat syntyä onnettomuuden aikana ja rikkoa luu ja sen läsnäolo pystyy muuttamaan koneiden käyttöä.

Ne toimivat suuressa mittakaavassa maankuoressa aiheuttaen murtumia geologisissa kivissä ja onnettomuuksissa tektonisen toiminnan ansiosta. Siksi ne ovat myös vastuussa planeetan jatkuvasti mallinnuksesta.

Viitteet

1. Olut, f. 2010. Materiaalimekaniikka. Viides. Painos. McGraw Hill. 7 - 9.
2. Fitzgerald, 1996. Materiaalimekaniikka. Alfa -omega. 21-23.
3. Giancoli, D.  2006. Fysiikka: sovellusten periaatteet. 6^tth  Ed. Prentice Hall. 238-242.
4. Hibbeler, R.C. 2006. Materiaalimekaniikka. Kuudes. Painos. Pearson -koulutus. 22 -25
5. Valera Negrete, J. 2005. Yleiset fysiikan muistiinpanot. Yksinäinen. 87-98.
6. Wikipedia. Leikkausrasitus. Toipunut: vuonna.Wikipedia.org.