Tuloksena oleva voima kuinka lasketut ja ratkaistut harjoitukset

Se pakottaa seurauksena oleva Kaikkien voimien summa, jotka toimivat samassa ruumiissa. Kun runko tai esine kohdistuu useiden voimien vaikutukseen samanaikaisesti, vaikutus tapahtuu. Näyttävät voimat voidaan korvata yhdellä voimalla, joka tuottaa saman vaikutuksen. Tämä ainutlaatuinen voima on tuloksena oleva voima, joka tunnetaan myös nimellä Net Force, ja sitä esitetään symbolilla F_{R -} .

Sen tuottama vaikutus F_{R -} Se riippuu koosta, suunnastaan ​​ja merkityksestään. Fyysiset suuruudet, joilla on suunta ja merkitys, ovat vektorien suuruuksia.

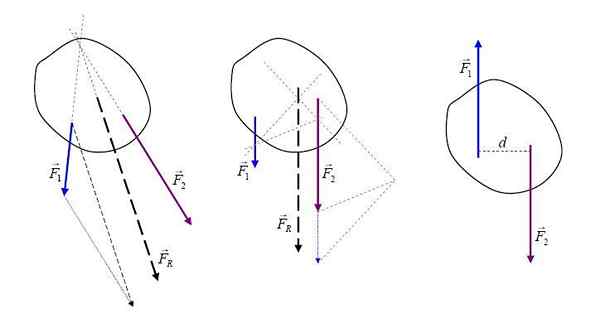Tuloksena olevat voimat. Kirjoittanut Ilevanat (https: // commons.Wikimedia.org/wiki/tiedosto: rejultanta.Jpg), Wikimedia Commons

Koska voimat, jotka vaikuttavat ruumiin ja vektorialueisiin, tuloksena oleva voima F_{R -}  Se on kaikkien voimien vektorisumma, ja sitä voidaan edustaa graafisesti nuolella, joka osoittaa sen suunnan ja merkityksen.

Tuloksena olevan voiman avulla useiden voimien kärsimyksen ongelmaa yksinkertaistetaan vähentämällä se yhdeksi voimiseksi, joka toimii.

[TOC]

Kaava

Tuloksena olevan voiman matemaattinen esitys on joukkojen kesävektori.

 F_{R -}= ∑F          (1)

 ∑F = f₁+ F₂+ F₃+.. F_N           (2)

F_{R -}= Tuloksena oleva voima

∑F = Joukkojen summa

N= Voimien lukumäärä

Tuloksena oleva voima voidaan edustaa myös Newtonin toisen lain yhtälöllä.

   F_{R -}= m.-lla          (3)

m= kehon massa

A = kehon kiihtyvyys

Jos yhtälö (1) korvataan yhtälössä (3), saadaan seuraavat yhtälöt:

∑F = m.-lla          (4)

F₁+ F₂+ F₃+.. F_{N =} m.-lla          (5)

Matemaattiset lausekkeet (4) ja (5) tarjoavat tietoa kehon tilasta hankkimalla vektorikiipeys -lla.

Kuinka tuloksena oleva voima lasketaan?

Tuloksena oleva voima saadaan sovellettaessa Newtonin toista lakia, joka vahvistaa seuraavan:

Voi palvella sinua: Etäisyysvoimat

Kehoon vaikuttava nettovoima on yhtä suuri kuin sen massan tuote, jonka se hankkii. (Yhtälö (3))

Kehon kiihtyvyydellä on sovelletun nettovoiman suunta. Jos kaikki kehossa toimivat voimat tunnetaan, se riittää lisäämään sen vektorisesti saadaan saadaan voimaa. Samoin, jos tuloksena oleva voima tunnetaan, se jakaisi sen kehon runkoon sen kiihtyvyyden saamiseksi.

Jos tuloksena oleva voima on tyhjä, runko on levossa tai vakiona. Jos tuloksena oleva voima vaikuttaa vartaloon, yksi voima on yhtä suuri kuin tämä voima F_{R -}=F.

Kun useat voimat vaikuttavat samaan runkoon, voiman vektorikomponentit on otettava huomioon, ja jos nämä voimat ovat yhdensuuntaisia ​​tai eivät.

Esimerkiksi, jos liu'utamme vaakasuoraan pöydälle asetetun kirjan. Vaakasuunnassa olevat voimat ovat ainoat, jotka tarjoavat kiihtyvyyden vartaloon. Kirjan pystysuora verkkovoima on nolla.

Jos kirjan sovelletulla voimalla on taipumus taulukon vaakatasoon, voima kirjoitetaan pystysuoraan ja vaakasuoraan komponenttiin perustuen.

Seurauksena oleva rinnakkaiset voimat 

Rinnakkaiset voimat, jotka vaikuttavat runkoon, ovat ne voimat, jotka vaikuttavat samaan suuntaan. Ne voivat olla kahden tyyppisiä yhtäläisiä tai vastakkaiseen suuntaan.

Kun vartaloon vaikuttavilla voimilla on sama suunta ja sama merkitys tai ovat vastakkaiseen suuntaan, tuloksena saatu voima saadaan suorittamalla voimien numeeristen arvojen algebrallinen summa.

Voi palvella sinua: sähkökenttävirta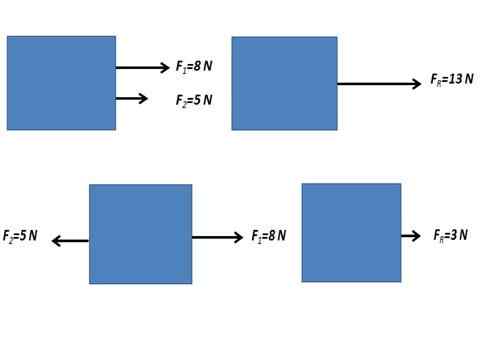Kahdesta yhdensuuntaisesta voimasta johtuva voima.

Ei -rinnakkaiset joukot

Kun kehon ei -rinnakkaiset voimat kohdistuvat, tuloksena olevilla voimilla on suorakaiteen muotoisia ja pystysuuntaisia ​​komponentteja. Matemaattinen lauseke nettovoiman laskemiseksi on:

F_{R -}²= (∑ f_x-A²+(∑ f_ja-A²            (6)

niin θ_x= ∑ f_ja / ∑ f_x         (7)

∑ f_x  ja ∑ f_x= Komponenttien algebrallinen summa x ja ja sovellettuja voimia

θ_x= kulma, joka muodostaa tuloksena olevan voiman F_{R -} Akselin kanssa x

Huomaa, että lausekkeesta (6) aiheuttamaa voimaa ei korosteta lihavoidulla kirjaimella, ja se johtuu siitä, että se vain ilmaisee numeerisen arvon. Osoite määritetään kulmassa θ_x.

Lauseke (6) on voimassa samassa tasossa toimiville voimille. Kun voimat toimivat avaruudessa, komponentti otetaan huomioon z -z voimaa, jos työskentelet suorakaiteen muotoisilla komponenteilla.

Ratkaisut

1. Määritä ruumiin aiheuttamat voimat, joihin kohdistetaan seuraavat kuvassa esitetyt voimat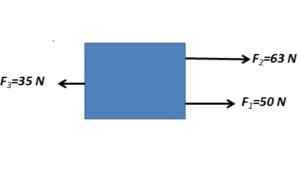

Rinnakkaiset voimat lisätään samassa mielessä ja vähennetään rinnakkaisvoiman kanssa vastakkaiseen suuntaan

F_{R -}= 63 n + 50 n - 35 n = 78n

Tuloksena olevan voiman suuruus on 78N vaakasuunnassa.

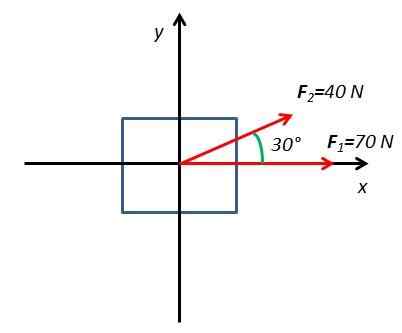
2.Laske kehosta johtuva voima kahden voiman vaikutuksen alaisena F_{1 ja} F₂. Voima F₁ Sen suuruus on 70N ja sitä levitetään vaakasuoraan. Voima F₂ Sen suuruus on 40N ja sitä levitetään 30 °: n kulmassa vaakatason suhteen.

Tämän harjoituksen ratkaisemiseksi piirretään vapaa kehon kaavio koordinaattiakseleilla x ja ja

Kaikki komponentit määritetään x ja ja ruumiissa toimivista voimista. Voima F₁ Sillä on vain vaakasuora komponentti akselilla x. Voima F₂ Siinä on kaksi komponenttia F_2x  ja f_{2 ja} jotka saadaan kulman 30 sini- ja kosinifunktioista.

Voi palvella sinua: kitka: tyypit, kerroin, laskenta, harjoitukset

F_1x = F₁=70N

F_2x = F₂ Cos 30 ° = 40 n.Cos 30 ° = 34,64n

F_1y = 0

F_{2 ja}= F₂ ilman 30 ° = 40 ilman 30 ° = 20n

∑ f_x =70N+34,64N = 104,64N

∑ f_ja=20n+0 = 20n

Kun akselin tuloksena olevat voimat on määritetty x ja ja Saadun voiman numeerinen arvo saadaan.

F_{R -}²= (∑ f_x-A²+(∑ f_ja-A²

Tuloksena oleva voima on joukkojen komponenttien kesäsumman neliöjuuri

F_{R -}= √ (104,64N)²+(20n)²

F_{R -}= 106 53N

Kulma, joka muodostaa tuloksena olevan voiman F_{R -} Se saadaan seuraavasta lausekkeesta:

θ_x= ruskea^-1(∑ f_ja / ∑ f_x-A

θ_x= niin^-1(20n - 104,64N) = 10,82 °

Tuloksena oleva voima F_{R -} Sen voimakkuus on 106,53N ja siinä on suunta määritetty 10,82 °: n kulmalla, joka muodostuu vaakasuunnassa.

Viitteet

1. Dola, g, duffy, m ja percival,. Fysiikka. Espanja: Heinemann, 2003.
2. Avison, J H. Fysiikan maailma. Intia: Thomas Nelson and Sons, 1989.
3. Mehu, m. Fyysinen prosessi. Yhdistynyt kuningaskunta: Nelson Thomas, 2002.
4. Yadav, s k. Tekniikan mekaniikka. Delhi: Discovery Publishing House, 2006.
5. Serway, R A ja Jewett, J W. Fysiikka tutkijoille ja insinööreille. Kalifornia, USA: Brooks/Cole, 2010.