Injektiivinen funktio, mistä se koostuu, mihin se on ja esimerkkejä

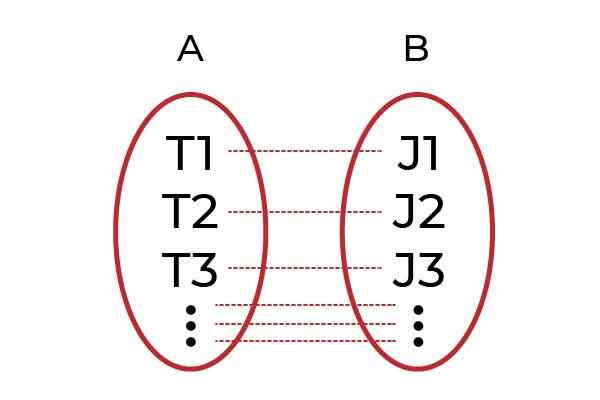
Eräs Injektiotoiminto Se on verkkotunnuksen elementtien suhde yhtenä osaan Codominium -elementtiä. Tunnetaan myös nimellä Function yksi kerrallaan ( yksitoista ), ovat osa funktioiden luokittelua koskevaa tapaa, jolla niiden elementit liittyvät.

Codominium -elementti voi olla vain kuva yhdestä domeenin elementistä, tällä tavoin riippuvaisen muuttujan arvoja ei voida toistaa.

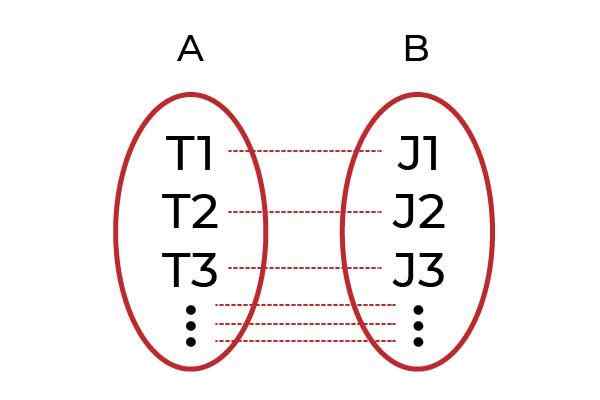
Lähde: Kirjoittaja.

Selkeä esimerkki olisi ryhmitellä miehiä ryhmässä A ja ryhmässä B kaikille pomoille. Toiminto F Se on se, joka yhdistää jokaisen työntekijän pomoonsa. Jos jokainen työntekijä liittyy eri pomoon F, niin F  Se on yksi Injektiotoiminto.

Harkita Injektiivinen Seuraavat on täytettävä funktioon:

∀ x₁  ≠ x₂   ⇒ f (x₁ ) ≠ F (x₂ -A

Tämä on algebrallinen tapa sanoa Kaikille x₁ erilainen kuin x₂ Sinulla on f (x₁ ) Erilainen kuin f (x₂ -A.

[TOC]

Mitkä ovat injektiiviset toiminnot?

Injektiivisuus on jatkuvien funktioiden ominaisuus, koska ne varmistavat kuvien jakamisen jokaiselle verkkotunnuksen elementille, olennainen näkökohta toiminnan jatkuvuudessa.

Kun piirtät akselin yhdensuuntaista viivaa X Injektiivisen toiminnon kaaviossa vain kuvaajaa tulisi koskettaa yhdessä pisteessä riippumatta siitä, minkä korkeuden tai suuruuden JA Viiva on piirretty. Tämä on graafinen tapa todistaa funktion injektiivisuus.

Toinen tapa testata, onko funktio Injektiivinen, tyhjentää riippumattoman muuttujan X Riippuvaisen muuttujan suhteen JA. Sitten se tulisi varmistaa, jos tämän uuden lausekkeen alue sisältää reaalilukut samaan aikaan kuin jokaiselle arvolle JA on yksi arvo X.

Järjestystoiminnot tai suhteet noudattavat muun muassa merkintää F: D_F→C_F

Se lukee F, joka menee D: stä_F C -_F

Missä funktio F Yhdistää sarjat Verkkotunnus ja Kodomini. Tunnetaan myös nimellä aloitusjoukko ja saapumisjoukko.

Voi palvella sinua: Satunnainen näytteenotto: metodologia, edut, haitat, esimerkit

Hallinto D -d_F  Sisältää riippumattoman muuttujan sallitut arvot. Codominium C_F  Se muodostuu kaikista käytettävissä olevista arvoista riippuvaiseen muuttujaan. Elementit C_F liittyen D -d_F  He tietävät miten Toimintoalue (r_F -A.

Toimintojen ilmastointi

Joskus funktio, joka ei ole injektio, voi läpikäyttää tiettyjä ilmastointia. Nämä uudet olosuhteet voivat muuttaa sen a Injektiotoiminto. Kaikenlaiset muutokset funktion verkkotunnukseen ja codominiumiin ovat päteviä, missä tavoitteena on täyttää injektiivisuusominaisuudet vastaavassa suhteessa.

Esimerkkejä injektiivisista toiminnoista ratkaistuilla harjoituksilla

Esimerkki 1

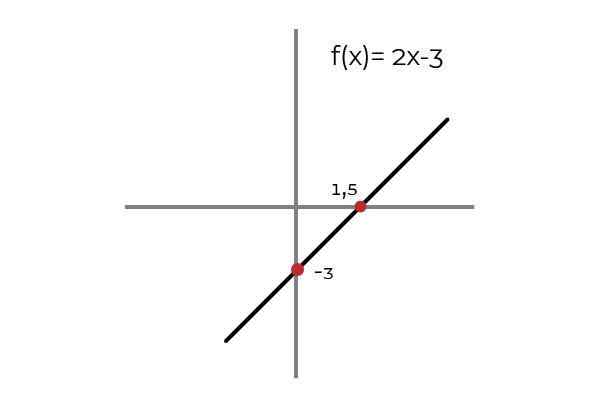
Olla toiminto F: r → R - linjalla määritelty F (x) = 2x - 3

V: [Kaikki todelliset numerot]

Lähde: Kirjoittaja.

Havaitaan, että kaikissa verkkotunnusarvoissa on kuva codominiumissa. Tämä kuva on ainutlaatuinen, mikä tekee injektiivisesta toiminnasta. Tämä koskee kaikkia lineaarisia funktioita (toiminnot, joiden suurempi muuttujan aste on yksi).

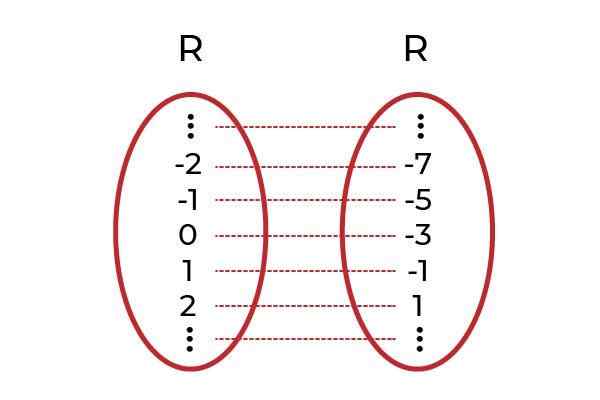Lähde: Kirjoittaja.

Esimerkki 2

Olla toiminto F: r → R - määritelty F (x) = x² +1

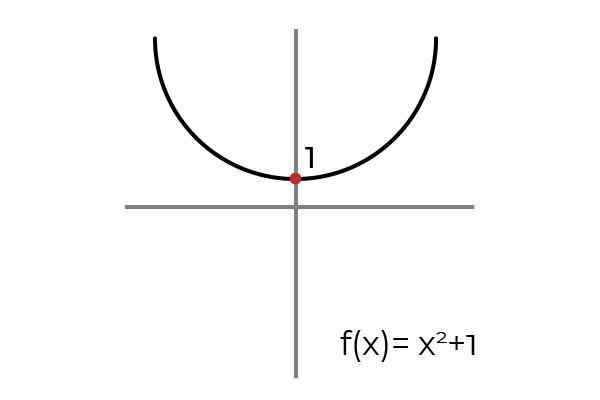Lähde: Kirjoittaja

Kun piirtät vaakaviivaa, havaitaan, että kaavio löytyy useammasta kuin yhdessä tilanteessa. Tämän vuoksi funktio F ei ole injektiivinen, kun se on määritelty  R - → R -

Funktion alue on ehdollinen:

                                               F: r⁺ TAI 0 → R -

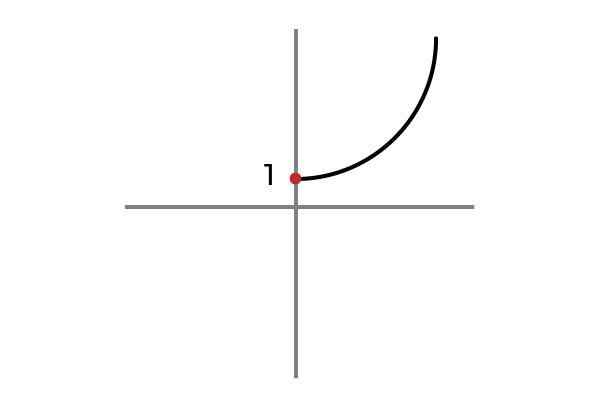Lähde: Kirjoittaja

Nyt riippumaton muuttuja ei ota negatiivisia arvoja, tällä tavalla sitä vältetään tulosten ja funktion toistamiseksi F: r⁺ TAI 0 → R - määritelty F (x) = x² + 1 on injektiivinen.

Toinen homologinen ratkaisu olisi rajoittaa aluetta vasemmalle, toisin sanoen funktiota ottamaan vain negatiiviset ja nolla -arvot.

Funktion alue on ehdollinen

                                               F: r^- TAI 0 → R -

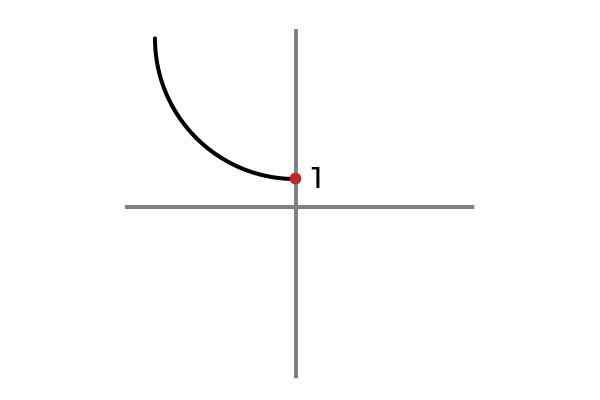Lähde: Kirjoittaja

Nyt riippumaton muuttuja ei ota negatiivisia arvoja, tällä tavalla sitä vältetään tulosten ja funktion toistamiseksi F: r^- TAI 0 → R - määritelty F (x) = x² + 1 on injektiivinen.

Trigonometrisillä funktioilla on käyttäytymistä samanlaisia ​​kuin aallot, missä on hyvin yleistä löytää arvojen toistoja riippuvaisessa muuttujassa. Erityisen ilmastoinnin kautta näiden toimintojen aikaisemman tietämyksen perusteella voimme rajoittaa alueen vastaamaan injektiivisuusolosuhteita.

Voi palvella sinua: Coplanares -pisteet: Yhtälö, esimerkki ja ratkaisut harjoitukset

Esimerkki 3

Olla toiminto F: [ -π/2, π/2 ] → R määritelty F (x) = cos (x)

Välein [[ -π/2 → π/2 - Kosinifunktio vaihtelee sen tuloksia nollan ja yhden välillä.

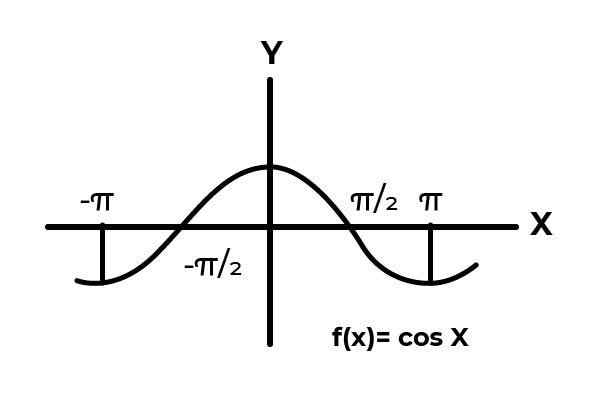Lähde: Kirjoittaja.

Kuten grafiikassa voidaan nähdä. Aloita tyhjästä x = -π/2 sitten saavuttaa enintään nolla. Se on jälkeen x = 0 että arvot alkavat toistaa, kunnes paluu nollaan sisään x = π/2. Tällä tavalla tiedetään F (x) = cos (x) ei ole injektiota Aikavälille [[ -π/2, π/2 - .

Kun tutkitaan funktiografiikkaa F (x) = cos (x) Väliajoja havaitaan, jos käyrän käyttäytyminen sopeutuu injektiokriteereihin. Kuten aikaväli

[0 , π -

Missä funktio vaihtelee välillä 1 --1, toistamatta mitään arvoa riippuvaisessa muuttujassa.

Tällä tavalla funktiotoiminto F: [0 , π ] → R määritelty F (x) = cos (x). Se on injektiivinen

On epälineaarisia funktioita, joissa vastaavat tapaukset esitetään. Rationaalisille ilmaisuille, joissa nimittäjällä on ainakin yksi muuttuja, on rajoituksia, jotka estävät suhteen injektiivisuuden.

Esimerkki 4

Olla toiminto F: r → R - määritelty F (x) = 10/x

Funktio on määritelty kaikille todellisille lukuille paitsi 0 joka esittelee määrittelemätöntä (sitä ei voida jakaa nollan välillä).

Kun lähestytään nollaa vasemmalla, riippuvainen muuttuja vie erittäin suuret negatiiviset arvot, ja heti nollan jälkeen riippuvaisen muuttujan arvot ottavat suuret positiiviset luvut.

Tämä häiriö tekee ilmaisun F: r → R - määritelty F (x) = 10/x

Älä injektiota.

Kuten aikaisemmissa esimerkeissä nähdään, arvojen poissulkeminen verkkotunnuksella "korjata" nämä määrittelyt. Nolla on jätetty pois verkkotunnuksesta, jättäen asetus- ja saapumisjoukot määriteltyinä seuraavasti:

R - 0 → R -

Missä R - 0 symboloi todellista paitsi joukkoa, jonka ainoa elementti on nolla.

Tällä tavalla ilmaus F: R - 0 → R - määritelty F (x) = 10/x on injektointi.

 Esimerkki 5

Olla toiminto F: [0 , π ] → R määritelty F (x) = sin (x)

Välein [0 , π - Sinusfunktio vaihtelee sen tuloksia nollan ja yhden välillä.

Voi palvella sinua: satunnaismuuttuja: käsite, tyypit, esimerkit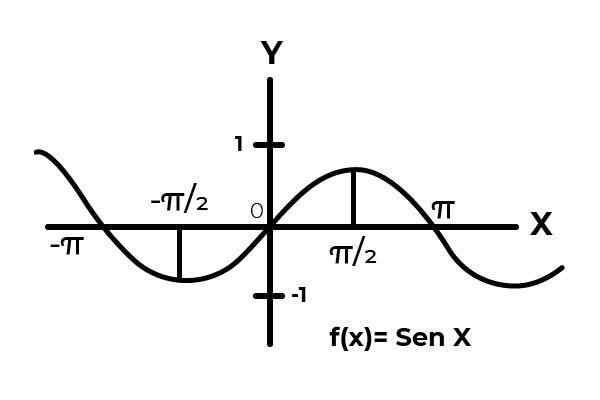Lähde: Kirjoittaja.

Kuten grafiikassa voidaan nähdä. Aloita tyhjästä x = 0 - sitten saavuttaa enintään x = π/2. Se on jälkeen x = π/2, että arvot alkavat toistaa, kunnes ne palaavat nollaan sisään x = π. Tällä tavalla tiedetään F (x) = sin (x) ei ole injektiota Aikavälille [0 , π - .

Kun tutkitaan funktiografiikkaa F (x) = sin (x) Väliajoja havaitaan, jos käyrän käyttäytyminen sopeutuu injektiokriteereihin. Kuten aikaväli  [[  π/2,3π/2  -

Missä funktio vaihtelee välillä 1 --1, toistamatta mitään arvoa riippuvaisessa muuttujassa.

Tällä tavalla funktio F: [  π/2,3π/2  ] → R määritelty F (x) = sin (x). Se on injektiivinen

Esimerkki 6

Varmista, onko toiminto F: [0, ∞) → R - määritelty F (x) = 3x² Se on injektiivinen.

Tässä yhteydessä ilmaisun alue on jo rajallinen. On myös havaittu, että riippuvaisia ​​muuttujan arvoja ei toisteta tällä aikavälillä.

Siksi voidaan päätellä F: [0, ∞) → R - määritelty F (x) = 3x²   Se on injektiivinen

Esimerkki 7

Tunnistaa, mikä seuraavista toiminnoista on

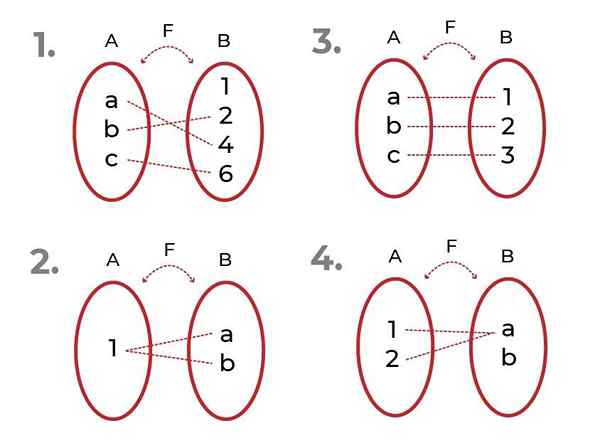Lähde: Kirjoittaja

1. Se on injektiivinen. Codominiumin liittyvät elementit ovat ainutlaatuisia riippumattoman muuttujan jokaiselle arvolle.
2. Se ei ole injektio. Aloitusjoukon useampaan kuin yhteen elementtiin liittyy elementtejä co -oominiumista.
3. Se on injektiivinen
4. Se ei ole injektio

Ehdotetut harjoitukset luokalle/talolle

Varmista, ovatko seuraavat toiminnot injektiota:

F: [0, ∞) → R - määritelty F (x) = (x + 3)²  

F: [ π/2,3π/2  ] → R määritelty F (x) = tan (x)

F: [ -π,π  ] → R määritelty F (x) = cos (x + 1)

F: r → R - linjalla määritelty F (x) = 7x + 2

Viitteet

1. Johdatus logiikkaan ja kriittiseen ajatteluun. Merrilee h. Lohi. Pittsburghin yliopisto
2. Matemaattisen analyysin ongelmat. Piotr Bilar, Alfred Witkowski. Wroclawin yliopisto. Pylväs.
3. Abstraktin analyysin elementit. Mícheál O'Searcoid PhD. Matematiikan laitos. University College Dublin, Beldfield, Dublind 4.
4. Johdatus logiikkaan ja deduktiivisten tieteiden metodologiaan. Alfred Tarski, New York Oxford. Oxford University Press.
5. Matemaattisen analyysin periaatteet. Enrique Linés Escardó. Toimituksellinen palautus. Vuoteen 1991. Barcelona, ​​Espanja.