Logaritmiset funktioominaisuudet, esimerkit, harjoitukset

Se logaritminen funktio Se on matemaattinen suhde, joka yhdistää jokaisen positiivisen todellisen lukumäärän x Logaritmillasi ja tukikohdassa -lla. Tämä suhde täyttää toiminnon vaatimukset: jokaisella verkkotunnukseen kuuluvalle elementille X on ainutlaatuinen kuva.

Siksi:

f (x) = y = log_-lla x , > 0: lla ja erilainen kuin 1.

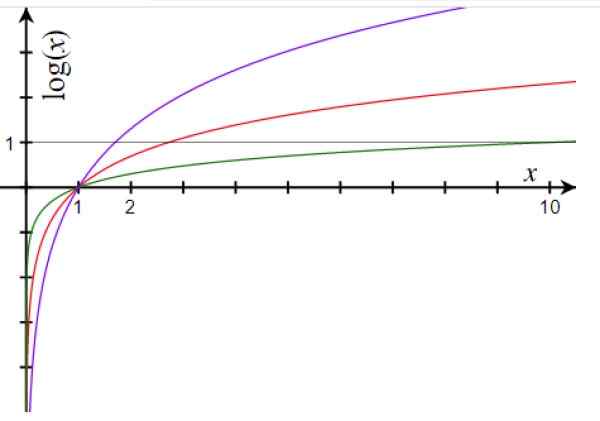
Kuvio 1. Logaritmitoimintokaavio pohjalle 10 (vihreä), pohja E (punainen) ja pohja 1.7 (violetti). Lähde: Wikimedia Commons.

Logaritmisen funktion pääominaisuudet ovat:

-Sen verkkotunnus ovat kaikki suurempia kuin 0, lukuun ottamatta 0. Toisin sanoen millään pohjalla ei ole logaritmia tai negatiivisia lukuja. Aikavälin muodossa:

Aurinko _F = (0, ∞+)

-Numeron logaritmi voi olla negatiivinen, positiivinen tai 0, joten sen alue tai reitti on:

Rgo _F = (-∞, ∞+)

-Logaritminen funktio kasvaa aina> 1: lle ja vähenee<1.

-Käänteinen jstk f (x) = loki_-lla x on eksponentiaalinen funktio.

Itse asiassa logaritmifunktio, joka perustuu, on potentiaalisen funktion käänteinen funktio:

F^-1(x) = a^ja

Logaritmiin perustuen -lla lukumäärä x, Se on numero ja johon tukikohta on nostettava -lla saada x.

-Peruslogaritmi on aina 1. Siten kaavio f (x) = loki_-lla x Aina leikkaa x -akseliin pisteessä (1.0)

-Logaritminen funktio on transsendentti eikä sitä voida ilmaista polynomina tai näiden osuudena. Logaritmin lisäksi tämä ryhmä sisältää muun muassa trigonometriset ja eksponentiaaliset toiminnot.

[TOC]

Esimerkit

Logaritminen funktio voidaan määrittää eri emäksillä, mutta eniten käytettyjä on 10 ja ja, missä ja Se on Eulerin lukumäärä, joka on yhtä suuri kuin 2 71828 .. .

Kun pohjaa 10 käytetään, logaritmia kutsutaan desimaalilogaritmiksi, mauton logaritmi, briggs tai yksinkertaisesti logaritmi kuivumaan.

Ja jos lukua E käytetään, sitä kutsutaan Neperian logaritmiksi, skotlantilainen matemaatikko John Napier, joka löysi logaritmit.

Voi palvella sinua: moninkertainen käänteinen: Selitys, esimerkit, ratkaisut harjoitukset

Jokaiselle käytetty merkintä on seuraava:

-Desimaalilogaritmi: Log₁₀ x = log x

-Neperian logaritmi: ln x

Kun toista tukikohtaa käytetään, se on ehdottoman välttämätöntä. Esimerkiksi, jos kyseessä on logaritmeja 2 tukikohdassa, se on kirjoitettu:

y = loki₂ x

Tarkastellaan numeroa 10 logaritmia kolmessa eri emäksessä tämän kohdan havainnollistamiseksi:

Loki 10 = 1

ln 10 = 2.30259

Hirsi₂ 10 = 3.32193

Yleiset laskimet tuovat vain desimaalien logaritmit (log) ja Neperian logaritmi (LN -toiminto). Internetissä on laskimia, joissa on muita emäksiä. Joka tapauksessa lukija voi vahvistaa sen avulla, että aikaisempien arvojen kanssa se on täytetty:

10¹ = 10

ja^2.3026 = 10.0001

2^3.32193 = 10.0000

Pienet desimaalien erot johtuvat logaritmin laskennassa otettujen desimaalien määrästä.

Logaritmien edut

Logaritmien käytön eduista on helppous, jonka ne tarjoavat suurten määrien kanssa, käyttämällä heidän logaritmiaan suoraan numeron sijasta.

Tämä on mahdollista, koska logaritmifunktio kasvaa hitaammin, kun numerot ovat suurempia, kuten arvostamme grafiikassa.

Joten jopa erittäin suurten määrien tapauksessa niiden logaritmit ovat paljon pienempiä ja pienten lukujen manipulointi on aina helpompaa.

Lisäksi logaritmit täyttävät seuraavat ominaisuudet:

-Tuote: loki (a.b) = log a + loki b

-Osamäärä: loki (a/b) = log a - log b

-Voima: loki a^{b -} = b.loki a

Ja tällä tavoin tuotteista ja osuuksista tulee pienempien lukujen summa ja vähennys, kun taas potentiaatio muuttuu yksinkertaiseksi tuotteeksi, vaikka teho on korkea.

Siksi logaritmit antavat ilmaista lukuja, jotka vaihtelevat erittäin suurilla arvoalueilla, kuten äänen voimakkuus, liuoksen pH, tähtien kirkkaus, sähkövastus ja Richterin maanjäristysten voimakkuus asteikko.

Voi palvella sinua: Ulkoiset vaihtoehtoiset kulmat: RAKENNUKSET JA TAKAUTUKSETKuva 2. Logaritmeja käytetään Richter -asteikolla maanjäristysten suuruuden kvantifioimiseksi. Kuva näyttää rakennuksen, joka on romahtunut Concepciónissa, Chilessä, vuoden 2010 maanjäristyksen aikana. Lähde: Wikimedia Commons.

Katsotaanpa esimerkki logaritmien ominaisuuksien käsittelystä:

Esimerkki

Löydä x: n arvo seuraavasta lausekkeesta:

log (5x +1) = 1 + log (2x-1)

Vastaus

Meillä on täällä logaritminen yhtälö, kun otetaan huomioon se, että tuntematon on logaritmi -argumentti. Se ratkaistaan ​​jättämällä yksi logaritmi tasa -arvon molemmille puolille.

Aloitamme asettamalla kaikki termit, jotka sisältävät "X" tasa -arvon vasemmalle, ja sellaiset, jotka sisältävät vain numerot oikealla:

loki (5x+1) - loki (2x -1) = 1

Vasemmalla puolella meillä on kaksi logaritmia, jotka voidaan kirjoittaa osamäärän logaritmina:

loki [(5x+1)/ (2x-1)] = 1

Oikealla on numero 1, jota voimme ilmaista log 10: ksi, kuten aiemmin näimme. Niin:

loki [(5x+1)/ (2x-1)] = log 10

Tasa -arvon toteuttamiseksi väitteet logaritmien on oltava samat:

(5x+1)/ (2x-1) = 10

5x + 1 = 10 (2x - 1)

5x + 1 = 20 x - 10

-15 x = -11

x = 11/15

Sovellusharjoitus: Richterin mittakaava

Vuonna 1957 Meksikossa tapahtui maanjäristys, jonka suuruus oli 7.7 Richter -asteikolla. Vuonna 1960 Chilessä tapahtui toinen suurimpi maanjäristys, 9.5.

Laske kuinka monta kertaa chileläinen maanjäristys oli voimakkaampi kuin Meksikossa, tietäen, että suuruus M_{R -} Richter -asteikolla se antaa kaava:

M_{R -} = loki (10⁴ Yo)

Ratkaisu

Maanjäristyksen Richter -asteikon suuruus on logaritminen funktio. Aiomme laskea kunkin maanjäristyksen voimakkuuden, koska meillä on rikkaat suuruudet. Tehdään se askel askeleelta:

Voi palvella sinua: Primo -numerot: Ominaisuudet, esimerkit, harjoitukset

-Meksiko: 7.7 = loki (10⁴ Yo)

Koska logaritmifunktion käänteinen on eksponentiaalinen, käytämme tätä tasa -arvon molemmille puolille selvitys I: n tarkoituksella, joka löytyy logaritmi -argumentista.

Koska ne ovat desimaalin logaritmeja, pohja on 10. Niin:

Oikealla, 10 ja loki (10⁴ I) Ne peruutetaan (kuten neliö- ja neliöjuuri), ovat: poistuminen:

10 ^7.7 = 10⁴ Yllyttää

Meksikon maanjäristyksen voimakkuus oli:

Yllyttää_M = 10 ^7.7 / 10⁴ = 10^3.7

 -Chili: 9.5 = loki (10⁴ Yo)

Sama menettely johtaa meidät Chilen maanjäristyksen I voimakkuuteen_CH-

Yllyttää_CH = 10 ^9.5 / 10⁴ = 10^5.5

 Nyt voimme verrata molempiin intensiteettejä:

Yllyttää_CH / Yo_M = 10^5.5 / 10^3.7 = 10^1.8 = 63.1

 Yllyttää_CH = 63.1. Yllyttää_M

Chilen maanjäristys oli noin 63 kertaa voimakkaampi kuin Meksiko. Koska suuruus on logaritmista, se kasvaa hitaammin kuin intensiteetti, joten ero 1 suuruudessa tarkoittaa 10 kertaa suurempaa seismisen aallon amplitudia.

Ero molempien maanjäristysten suuruuksien välillä on 1.8, siksi voisimme odottaa intensiteettieroja lähempänä 100 kuin 10, kuten käytännössä tapahtui.

Itse asiassa, jos ero olisi ollut 2 tarkalleen, Chilen maanjäristys olisi ollut 100 kertaa voimakkaampi kuin meksikolainen.

Viitteet

1. Carena, m. 2019. Preuniversity -matematiikan käsikirja. Rannikon kansallinen yliopisto.
2. Figuera, J. 2000. 1. matematiikka. Monipuolinen vuosi. Co-bo-painikkeet.
3. Jiménez, r. 2008. Algebra. Prentice Hall.
4. Larson, r. 2010. Muuttujan laskenta. 9NA. Painos. McGraw Hill.
5. Stewart, J. 2006. Precculment: Laskentamatematiikka. Viides. Painos. Cengage -oppiminen.