Matematiikka

Todellinen todellisen muuttujan toiminto ja sen graafinen esitys

Todellinen todellisen muuttujan toiminto ja sen graafinen esitys

Eräs Todellinen todellinen muuttujatoiminto Ota lukumäärä reaalilukujoukkoon kuuluva numero ja yhdistää sen toiseen arvoon, myös todellinen, ainutlaatuisen kirjeenvaihtosäännön kautta. Tämä tarkoittaa, että todellinen numero saa tämän säännön kautta ainutlaatuisen kuvan.

Numeeriset lähtömuuttujat on yleensä osoitettu kirjaimella X, kun taas niiden kuva on kirjain ja. Toisaalta niitä yhdistävään kirjeenvaihtosääntöön kutsutaan myös johonkin muuhun aakkosen kirjaimeen, kuten "F" -toiminto, vaikka toista voidaan käyttää.  Kompaktissa merkinnöissä se on kirjoitettu:

F: x → y = f (x)

Kuvio 1. Kaavio todellisesta polynomifunktiosta

Muuttujalle  x sitä kutsutaan itsenäinen muuttuja, samalla kun ja Se on riippuva muuttuja. Toiminto voidaan ilmaista monin tavoin, esimerkiksi tällaisen matemaattisen lausunnon avulla:

  • f (x) = 2x −3
  • H (x) = −3x2

Toinen ilmaisumuoto on kuvaajan kautta, joka on erittäin hyödyllinen, koska sen avulla voit arvostaa yhden yhtenäisyyden toiminnan käyttäytymistä. Kaavion rakentaminen on hyvin yksinkertaista käyttämällä Cartesian koordinaattijärjestelmää, jossa ikätoverit [x, f (x)] esitetään pisteenä tasolla. Sitten he liittyvät pehmeällä ja jatkuvalla viivalla, näet kuinka toiminto on.

Esimerkit

Kraafin rakentamiseksi voit turvautua arvotaulukkoon, jossa graafiset kohdat sijoitetaan. Valittujen muuttujien X arvot, jotka kuuluvat funktion alueelle, toisin sanoen ne, jotka korvataan kaavassa, osoittavat puolestaan ​​reaalilukuja.

Kun X: n arvot on valittu, sen kuva y = f (x) määritetään, ja tällä tavoin saadaan pisteparit [x, f (x)], jotka ovat graafisia.

Voi palvella sinua: Homografinen toiminto: Kuinka kuvaaja, ratkaistut harjoitukset

Jotkut kohdat ovat tärkeitä ja tulisi sisällyttää taulukkoon: ne, joissa kuvaaja leikkaa koordinaattiakselit, jos ne ovat, koska kaikki toiminnot eivät leikkaa niitä.

Laske ne jatka seuraavasti:

-Risteys akselin ja: x = 0 tehdään funktiokaavassa ja vastaava arvo lasketaan.

-Risteys x -akselilla: Y = 0 tehdään ja yhtälö f (x) = 0 on ratkaistu.

Seuraavaksi piirretään Cartesian -koordinaattijärjestelmä ja jokainen piste on piirretty, jotka sitten liitetään pehmeällä ja jatkuvalla viivalla, jos mahdollista.

Esimerkki 1

Rakenna arvotaulukko ja seuraavan toiminnon kaavio:

f (x) = x2 −4

Ennen aloittamista sinun on löydettävä funktion alue, joka on reaaliarvojen joukko, jolle funktio on olemassa. Koska se on neliömäinen funktio, kaikilla todellisiin numeroihin kuuluvassa x -arvossa on todellinen kuva F (x): n mukaan.

Sitten taulukko voidaan rakentaa valitsemalla mikä tahansa X -arvo, ja yksinkertaisin asia on aloittaa kuvaajan risteyksistä akselien kanssa, jos niitä on. Kun ne on löydetty, sitten muita kohtia pyritään täyttämään taulukko.

X = 0

f (0) = -4

Siksi taulukon ensimmäinen kohta on (0, -4). Tämä on kaavion leikkaus akselin kanssa ja.

Y = 0: lle

Sitten y = 0 tehdään ja tulokset ratkaisee yhtälö:

x2 −4 = 0

x2 = 4

Tämän yhtälön ratkaisut ovat: x1= 2 ja x2= -2. Siksi X -akselin kanssa on kaksi risteystä, jotka ovat pisteitä: (−2,0) ja (2.0).

Voi palvella sinua: Täydelliset numerot: Kuinka tunnistaa ne ja esimerkkejä

Nyt löydät lisää pisteitä lisättäväksi arvotaulukkoon:

X = 1

f (1) = (1)2 - 4 = −3

X = - 1

f (−1) = (−1)2 - 4 = −3

X =  3

F (3) = (3)2 - 4 = 5

X =  -3

f (−3) = (−3)2 - 4 = 5

Arvotaulukko

Seuraava taulukko näyttää saadut kohdat, jotka rakentavat f (x) -kaavion:

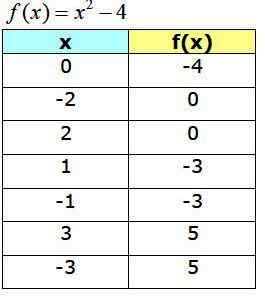Toimintokaavio F (x) = x2 −4

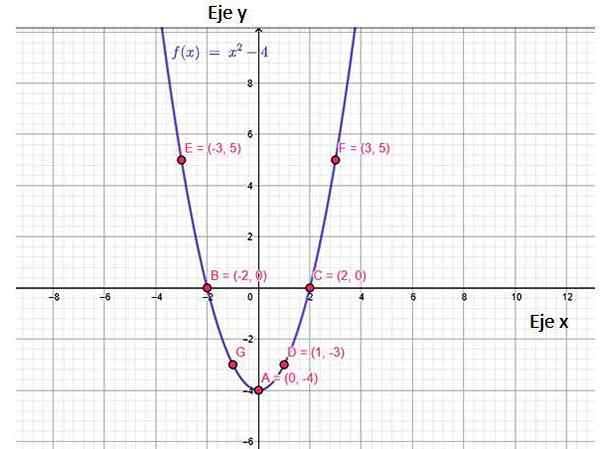Kuva 2. Toiminto f (x) -toimintokaavio, joka näyttää joitain siihen kuuluvia pisteitä, mukaan lukien risteykset akselien kanssa. Lähde: f. Zapata, Geogebran kautta.

Tämän funktion kaavio on vertaus, joka avautuu ja jolla on minimipiste, nimeltään kärki, koordinaattien (0, −4). On mielenkiintoista huomata, että f (x): n arvot alkavat y = -4 -∞. Tämä on alue toiminnasta.

Kaaviosta voidaan päätellä, että funktio on jatkuva, vähenee aikavälillä (−∞, 0) ja kasvaa sieltä.

Esimerkki 2

Jos funktion kaavio on mahdollista tietää sen alue, sen alue, sen risteykset akselien kanssa ja visualisoida sen yleinen käyttäytyminen (kasvu ja väheneminen).

Alla on polynomifunktion kuvaaja:

f (x) = - x4+4x2+1

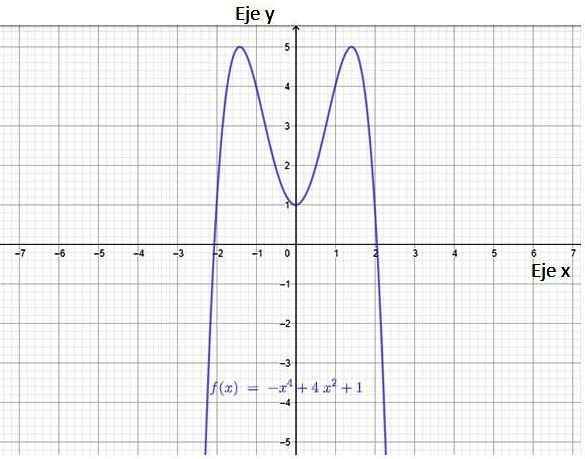Kuva 3. Polynomifunktion kaavio. Lähde: f. Zapata Geogebran kautta.

Kuvan perusteella seuraa, että funktiolla on kaksi risteystä X-akselin kanssa, pisteet (-2,0) ja (2.0). Sillä on myös risteys Y -akselin, pisteen kanssa (0,1).

Polynomifunktion alue on täydellinen joukko reaalilukuja, varoitetaan myös, että funktio on jatkuva ja symmetria pystysuoran akselin ympärillä. Todellakin voidaan varmistaa, että tämä toiminto on Symmetria. Toiminto on, vaikka se tapaa:

Voi palvella sinua: vihreä lause, esittely, sovellukset ja harjoitukset

f (x) = f (-x)

Lukija voi varmistaa, että korvaamalla -x toiminnossa, sitä ei muuteta.

On olemassa kaksi mielenkiintoista pistettä, jotka ovat Y = 5: n korkeudessa, ovat funktion enimmäisarvoja. Tämän funktion alue, toisin sanoen muuttujan ottama arvojoukko ja ulottuu -∞: sta y = 5 tarkasti.

Tietääksesi x: n arvot, joiden kuva on y = 5, tämä arvo korvataan funktiossa:

5 = - x4+4x2+1

Ja tämä yhtälö saadaan:

- x4 + 4x2 - 4 = 0

Joiden ratkaisut ovat −ity ja + √2. No, funktio on:

-Kasvava X -∞: sta x = −√2: een

-Vähentyvä Alkaen x = −ksu x = 0

-Kasvava Kohdasta x = 0 - x = + √2

-Vähentyvä Alkaen x = + √2 eteenpäin.

Liikuntaa

Rakenna seuraavan toiminnon kaavio:

f (x) = √ (x-5)

Ratkaisu

Ensin sinun on määritettävä funktion alue, tietääksesi, mitkä X: n arvot voidaan valita taulukon rakentamiseksi. Ehdotetun funktion tapauksessa juuren sisällä olevan määrän on aina oltava positiivinen tai yhtä suuri kuin 0, siksi:

x - 5 ≥ 0

x ≥ 5

Siksi taulukossa voidaan valita vain 5 tai yhtä suuret arvot. Mitä tulee risteyksiin koordinaattiakselien kanssa, ainoa mahdollisuus on tehdä y = 0 ja sitten x = 5.

On turhaa tehdä x = 0 tälle toiminnolle, koska tämä arvo ei kuulu verkkotunnukseen.

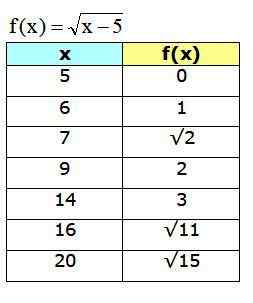
Saatu kaavio on:

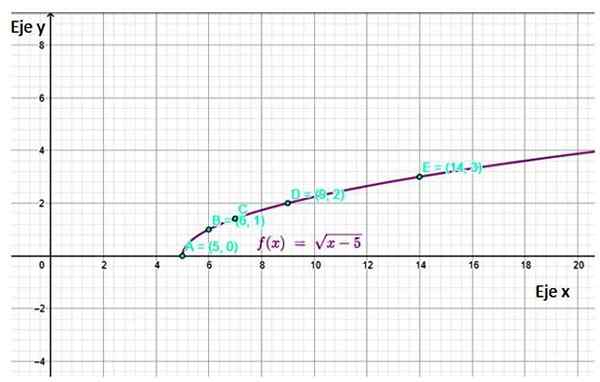Kuva 4. Funktiokaavio F (x), joka näyttää joitain taulukossa laskettuja pisteitä. Lähde: f. Zapata Geogebran kautta.

Viitteet

  1. E-math-vyöhyke. Toimintotyypit. Toipunut: Emathzone.com.
  2. Hoffman, J.G. Matematiikan aiheiden valinta. Ed. Spphinx.
  3. Matematiikka on hauskaa. Commons Function -viite. Toipunut: Mathisfun.com.
  4. Requena, b. Maailmankaikkeuden kaavat. Toimintotyypit. Toipunut: UniversOformulat.com.
  5. Stewart, J. 2006. Precculment: Laskentamatematiikka. Viides. Painos. Cengage -oppiminen.