Liiallinen toiminto, ominaisuudet, esimerkit

Eräs liiallinen toiminto Se on mikä tahansa suhde, jossa jokainen codominiumiin kuuluva elementti on ainakin yhden verkkotunnuksen elementin kuva. Tunnetaan myös nimellä Function noin, Ne ovat osa funktioiden luokittelua koskevaa tapaa, jolla heidän elementinsä liittyvät.

Esimerkiksi toiminto F: a → B - määritelty F (x) = 2x

Jota luetaan "F Se menee -Lla siihen asti kun B - määritelty F (x) = 2x "

Kosketa määrittele lähtö- ja saapumisjoukot A ja B.

V: 1, 2, 3, 4, 5 Nyt arvot tai kuvat, jotka jokainen näistä elementeistä vapautetaan, kun arvioidaan F, Ne ovat codominiumin elementtejä.

F (1) = 2

F (2) = 4

F (3) = 6

F (4) = 8

F (5) = 10

Muodostaen siten sarjan B: 2, 4, 6, 8, 10

Se voidaan päätellä sitten:

F: 1, 2, 3, 4, 5  → 2, 4, 6, 8, 10 määritelty F (x) = 2x on liiallinen funktio

Kodinionin jokaisen elementin on oltava vähintään yksi riippumattoman muuttujan toiminto kyseisen toiminnon kautta. Kuvaa rajoittamista ei ole, codominium -elementti voi olla kuva useammasta kuin yhdestä verkkotunnuksen elementistä ja jatkaa käsittelyä a liiallinen toiminto.

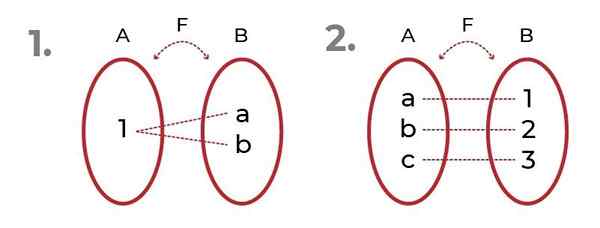
Kuva näyttää 2 esimerkkiä onjektiivitoiminnot.

Lähde: Kirjoittaja

Ensimmäisessä havaitaan, että kuvat voidaan viitata samaan elementtiin, vaarantamatta Liiallinen toiminnasta.

Toisessa näemme tasapuolisen jakautumisen verkkotunnuksen ja kuvien välillä. Tämä aiheuttaa Bijektiivifunktio, missä kriteerit Injektiivinen funktio ja liiallinen funktio.

Toinen tapa tunnistaa onjektiivitoiminnot, on tarkistaa, onko codominium yhtä suuri kuin funktion sijoitus. Tämä tarkoittaa, että jos saapumisjoukko on yhtä suuri kuin funktion tarjoamat kuvat arvioitaessa riippumatonta muuttujaa, Funktio on ylihaitos.

[TOC]

Ominaisuudet

Harkita Liiallinen Seuraavat on täytettävä funktioon:

Olla F: D_F → C_F

∀ B ℮ C_F  JA ℮  D -d_F   / F (a) = b

Tämä on algebrallinen tapa selvittää se Kaikille "B", joka kuuluu C: lle_F On "a", joka kuuluu D_F  sellainen, että "A": ssä arvioitu F -funktio on yhtä suuri kuin "B". 

Se voi palvella sinua: radikaalit ominaisuudet

Ylijulkaisu on toimintojen erityispiirte, jossa codominium ja sijoitus ovat samanlaisia. Siten toiminnossa arvioidut elementit muodostavat saapumisjoukon.

Toimintojen ilmastointi

Joskus funktio, joka ei ole Liiallinen, voi käydä läpi tiettyjen ilmastointien. Nämä uudet olosuhteet voivat muuttaa sen a liiallinen toiminto.

Kaiken tyyppiset muutokset funktion verkkotunnukseen ja codominiumiin ovat päteviä, missä tavoitteena on täyttää vastaavan suhteen ylijulkaisuominaisuudet.

Esimerkkejä: Ratkaisut harjoitukset

Vastaamaan Liiallinen Erilaisia ​​ilmastointitekniikoita tulisi soveltaa, tämä varmistaakseen, että jokainen Codominium -elementti on funktion kuvien joukossa.

Harjoitus 1

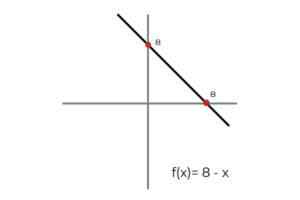
• Olla toiminto F: r → R - linjalla määritelty F (x) = 8 - x

V: [Kaikki todelliset numerot]

Lähde: Kirjoittaja

Tässä tapauksessa funktio kuvaa jatkuvaa viivaa, joka kattaa kaikki todelliset numerot sekä niiden verkkotunnuksella että alueella. Koska funktion sijoitus R -_F Se on yhtä suuri kuin codominium R - Voidaan päätellä, että:

F: r → R - linjalla määritelty F (x) = 8 - x on liiallinen toiminto.

Tämä koskee kaikkia lineaarisia funktioita (toiminnot, joiden suurempi muuttujan aste on yksi).

Harjoitus 2

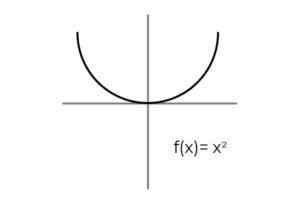
• Tutki toimintaa F: r → R - määritelty F (x) = x² : Määritä, onko se a liiallinen toiminto. Jos se ei ole, näytä tarvittava ilmastointi siitä, että se olisi liian.

Lähde: Kirjoittaja

Ensimmäinen asia, joka on otettava huomioon F, joka koostuu todellisista numeroista R -. Ei ole mitään keinoa heittää negatiivista arvoa, joka sulkee pois negatiiviset todelliset arvot mahdollisten kuvien joukossa.

Väliaika codominium [0 , ∞ -. Sitä vältetään jättämään co -alomion elementit liittymättä läpi F.

Kuvat toistetaan riippumattoman muuttujan, kuten x = 1 ja x = - 1.  Mutta tämä vaikuttaa vain Injektiivisuus  toiminnasta, ei ole ongelma tämän tutkimuksen kannalta.

Voi palvella sinua: peräkkäiset johdannaiset

Tällä tavalla voidaan päätellä, että:

F: r  →[0, ∞ -A määritelty F (x) = x²    Se on ylijohtotoiminto

Harjoitus 3

• Määritä codominium -olosuhteet, jotka he tekisivät liiallinen toimintoihin

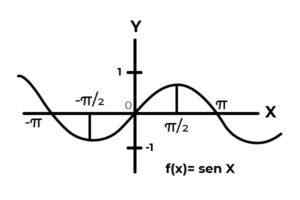
F: r  → R - määritelty F (x) = sin (x)

F: r  → R - määritelty F (x) = cos (x)

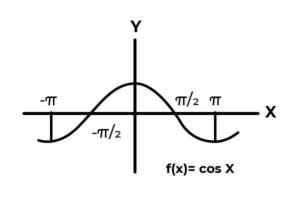Lähde: Kirjoittaja Lähde: Kirjoittaja.

Trigonometristen funktioiden käyttäytyminen on samanlainen kuin aaltojen käyttäytyminen, ja se on hyvin yleinen löytääkseen kuvien välisen riippuvan muuttujan toistot. Myös useimmissa tapauksissa funktion alue on rajoitettu yhteen tai useampaan todellisen viivan alaan.

Näin on sini- ja kosinitoiminnot. Missä niiden arvot vaihtelevat aikavälillä [-1, 1]. Mainittu aikavälin on eheä codominium funktion kirjekuoren saavuttamiseksi.

F: r  →[-Eleven] määritelty F (x) = sin (x)  Se on ylijohtotoiminto

F: r  →[-Eleven]määritelty F (x) = cos (x) Se on ylijohtotoiminto

Harjoitus 4

• Tutki toimintaa

F: [0, ∞ -A → R - määritelty F (x) = ± √x   tarkoita, jos se on a liiallinen toiminto

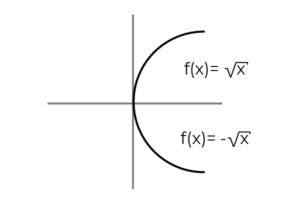Lähde: Kirjoittaja

Toiminto F (x) = ± √x  Sillä on erityisyys, joka määrittelee 2 riippuvaa muuttujaa jokaisessa "x" -arvossa . Eli alue saa 2 elementtiä jokaiselle, joka suoritetaan verkkotunnuksessa. Jokaiselle "x" -arvolle positiivinen ja negatiivinen arvo on varmistettava jokaiselle "x" -arvolle.

Aloituskokoonpanon tarkkailemisessa todetaan, että domeenia on jo rajoitettu, tämä voidaan välttää määrittelemättömät määrät, jotka on tuotettu arvioitaessa negatiivista lukua vääntömomentin juuressa.

Kun varmennetaan funktion alue, se osoittaa, että jokainen Codominium -arvo kuuluu alueelle.

Tällä tavalla voidaan päätellä, että:

F: [0, ∞ -A → R - määritelty F (x) = ± √x  Se on ylijohtotoiminto

Voi palvella sinua: samanaikaiset vektorit: ominaisuudet, esimerkit ja harjoitukset

Harjoitus 4

• Tutki toimintaa F (x) = ln x  tarkoita, jos se on a liiallinen toiminto. Ehdota saapuminen ja lähtö asetetaan mukauttamaan funktiota liiallisuuskriteereihin.

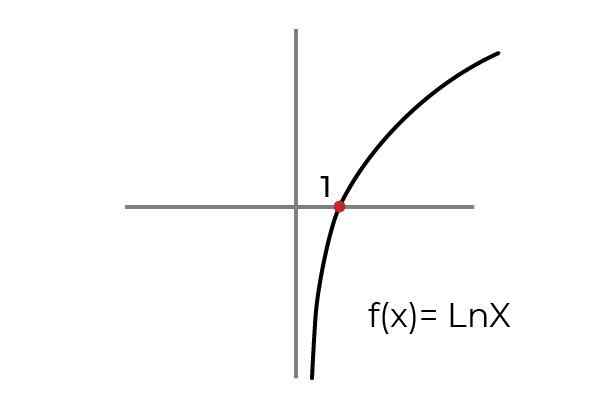Lähde: Kirjoittaja

Kuten kaaviossa esitetään, funktio F (x) = ln xon määritelty "x": n arvoihin suurempi kuin nolla. Vaikka "ja" tai kuvien arvot voivat ottaa minkä tahansa todellisen arvon.

Tällä tavoin voimme rajoittaa aluetta F (x) = välein (0 , ∞ -A

Vaikka funktion sijoitus voidaan ylläpitää reaalilukujen sarjana R -.

Tämän huomioon ottaen voidaan päätellä, että:

F: [0, ∞ -A → R - määritelty F (x) = ln x  Se on ylijohtotoiminto

Harjoitus 5

• Tutki absoluuttisen arvon funktiota F (x) = | X | ja nimeä saapumis- ja lähtöjoukot, jotka on kerätty Allegivery -kriteereihin.

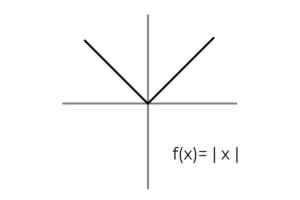Lähde: Kirjoittaja

Funktion alue täyttyy kaikille todellisille lukuille R -. Tällä tavoin ainoa ilmastointi on suoritettava codominiumissa ottaen huomioon, että absoluuttinen arvofunktio ottaa vain positiivisia arvoja.

Funktion codominium vahvistetaan tasoittaen sen saman alueen

[0 , ∞ -A

Nyt voidaan päätellä, että:

F: [0, ∞ -A → R - määritelty F (x) = | X |  Se on ylijohtotoiminto

Ehdotetut harjoitukset

1. Varmista, ovatko seuraavat toiminnot liiallinen:

• F: (0, ∞ -A → R - määritelty F (x) = log (x + 1)
• F: r → R - määritelty F (x) = x³
• F: r →[1, ∞ -A  määritelty F (x) = x²  + 1
• [0, ∞ -A → R - määritelty F (x) = log (2x + 3)
• F: r → R - määritelty F (x) = sek x
• F: R - 0 → R - määritelty F (x) = 1 / x

Viitteet

1. Johdatus logiikkaan ja kriittiseen ajatteluun. Merrilee h. Lohi. Pittsburghin yliopisto
2. Matemaattisen analyysin ongelmat. Piotr Bilar, Alfred Witkowski. Wroclawin yliopisto. Pylväs.
3. Abstraktin analyysin elementit. Mícheál O'Searcoid PhD. Matematiikan laitos. University College Dublin, Beldfield, Dublind 4
4.  Johdatus logiikkaan ja deduktiivisten tieteiden metodologiaan. Alfred Tarski, New York Oxford. Oxford University Press.
5.  Matemaattisen analyysin periaatteet. Enrique Linés Escardó. Toimituksellinen palautus. Vuoteen 1991. Barcelona, ​​Espanja.