Matematiikka

Vektoritoiminnot

Mitkä ovat vektoritoiminnot?

Eräs vektoritoiminto parametri t, Se on funktio, jonka alue on todelliset arvot t, kun taas reitin muodostuu muodon vektorit r - (t-A. Tällainen funktio voidaan ilmaista seuraavasti:

r - (t) = f (t-A Yllyttää + g (t-A J - + H (t-A k -k -

Missä Yllyttää, J - ja k -k - Ne ovat yksikkövektoreita tilan kolmessa pääryhmässä, ja toiminnot F, G ja H ovat muuttujan todellisia toimintoja t. Merkintä käyttää rohkeaa vektorien suuruuden erottamiseksi.

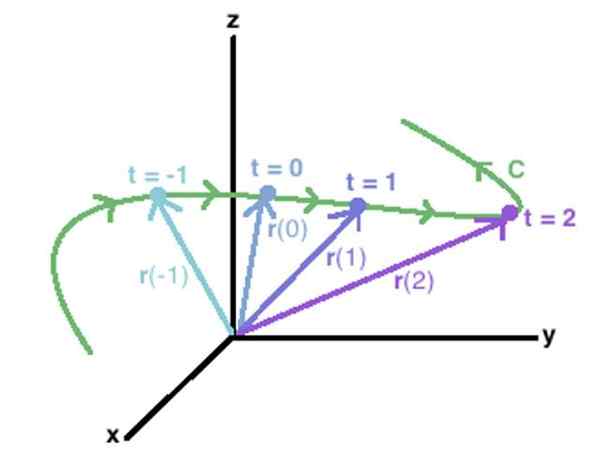Avaruuden vektoritoimintoa voidaan käyttää kuvaamaan C -käyrää yhdistämällä kunkin vektorin äärimmäiset pisteet, jotka määritetään mainitulla funktiolla. Lähde: Wikidot.

Toinen tapa osoittaa vektorifunktiota on neliöhakeiden kautta:

r - (t) = t), G (t), H (t>>

Vektoritoimintoja voidaan käyttää käyrien tutkimiseen tasossa ja tilassa, kuten liikkuva esinettä seuraavaa etenemissuuntausta. Esimerkki on projisoidun pallon kuvaama vertaus alkuperäisellä nopeudella, painovoimassa.

Jos haluat tietää pallon sijainnin jokaisen ajanjakson ajan t, Vektoritoiminto kahdella komponentilla, yksi vaakasuora ja yksi pystysuora:

r - (t) = x (t-A Yllyttää + ja(t-A J -

Molemmat x (t) kuten y (t) Ne ovat aikatoimintoja t. Siten kun liityt kunkin vektorin äärimmäisiin pisteisiin r -(t) Mahdollinen, muodosta vertaus, jonka pallo kuvataan tasolla Xy.

Konsepti ulottuu helposti avaruuden C -käyrälle, kuten yllä olevassa kuvassa. Vektorit ilmestyvät siinä r - (-1), r - (0), r - (1) r - (2), jonka päät piirtävät C -käyrän, piirretty vihreäksi.

Rajoitukset, johdetut ja integraali vektoritoiminnot

Laskentatyökaluja, joita sovelletaan todellisiin muuttuviin toimintoihin, voidaan soveltaa myös vektoritoimintoihin.

Voi palvella sinua: tekijä

Vektoritoiminnon raja

Vektoritoimintoraja r - (t) = f (t-A Yllyttää + g (t-A J - + H (t-A k -k -, Kun T → A, se on määritelty:

$\dpi110 \displaystyle \lim_t \to a\textbfr(t)=\left [ \displaystyle \lim_ t\to a f(t)\right ]\textbfi+\left [ \displaystyle \lim_ t\to a g(t)\right ]\textbfj+\left [ \displaystyle \lim_ t\to a h(t)\right ]\textbfk$

Olettaen, että F: n vastaavat rajat (t), G (t) ja H (t), kun t → a.

Johdettu vektoritoiminnosta

Vektorifunktiosta johdettu määritelmä r - (t) = f (t-A Yllyttää + g (t-A J - + H (t-A k -k - Se on analoginen todellisen muuttujan todellisen funktion johdannaisen kanssa. Kutsumus r -'(t) mainitulle johdannaiselle, sinulla on:

$\dpi110 \mathbfr'(t)=\displaystyle \lim_\Delta t \to 0\frac\mathbfr(t+\Delta t)-\mathbfr(t)\Delta t$

Johdannainen on olemassa aina, kun edellinen raja on olemassa, ja jos on, funktio r -(t) on erilainen t.

Vektoritoiminnon integraali

Olla r - (t) = f (t-A Yllyttää + g (t-A J - + H (t-A k -k - vektoritoiminto, jolloin funktiot f, g ja h ovat integroitavissa t.

Niin:

$\dpi110 \int \mathbfr(t)dt =\left [ \int f(t)dt \right ]\mathbfi+\left [ \int g(t)dt \right ]\mathbfj+\left [ \int h(t)dt \right ]\mathbfk+\mathbfC$

Kanssa:

C = c₁Yllyttää + c₂J -

Mikä tarkoittaa, että integraatiovakio on myös vektori, mutta vakio.

Vektoritoimintoesimerkit

Esimerkki 1

Sinulla on annettu vektoritoiminto r - (t) = 3 sekuntia t Yllyttää + 2TAN t J -. Se on mahdollista arvioida erilaisille t -arvoille, kuten t = π/4 ja t = π, aiheuttaen vektoreita r - (π/4) ja r - (π):

r - (π/4) = 3 sekuntia (π/4) Yllyttää + 2TAN (π/4) J - = 3√2 Yllyttää + 2 J -

r - (π) = 3 sekuntia (π) Yllyttää+2tan (π) J - = - 3 Yllyttää

kuitenkin, r - (t) Sitä ei ole arvoille t = ∓π/2, ∓3π/2, ∓5π/2…, koska SEC -funktio t = 1 /cos t Sitä ei ole määritelty, onko se niin t = SEN t / cos t.

Siksi r (t) -funktion alue on kaikki T: n todelliset arvot, paitsi muodon arvot:

∓ (2n+1) π/2; N = 0, 1, 2, .. .

Funktion kuvaaja on hyperbola:

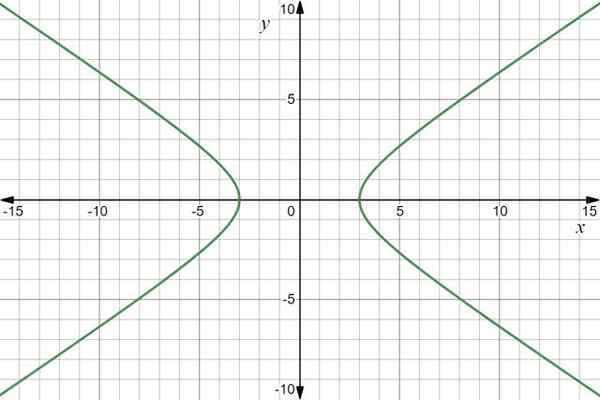Vektoritoimintokaavio r - (t) = 3 sekuntia t Yllyttää+2 tan t J -. Lähde: f. Zapata Desmosin kautta.

Esimerkki 2

Kaltevassa ammuksen käynnistämisessä mobiili -sijainti on vektoritoiminto r - (t) = x (t-A Yllyttää + ja(t-A J - . Olettaen, että ilmankestävyys ei puutu ja että painovoima on ainoa voima, joka vaikuttaa matkapuhelimeen, vaakasuora liike on tasainen suorakulmainen, kun taas pystysuora kiihtyy tasaisesti, koska se on g = 9.8 m/s² Kiihtyvyysarvo. Tämä kiihtyvyys on pystysuora kohti maata.

Voi palvella sinua: johdannaisäännöt (esimerkkien kanssa)

Tässä tapauksessa toiminnot x (t) ja (t) Ne ovat vastaavasti:

x (t) = x_jompikumpi + v_härkä∙ T
ja (t) = y_jompikumpi + v_Oy∙ T - ½ GT²

Määrät v_härkä ja v_Oy Ne ovat vektorifunktion komponentteja, jotka kuvaavat liikkuvan nopeuden jatkuvasti:

v (t) = V_x(t-A Yllyttää + v_ja(t-A J -

Kanssa-

v_härkä = v_jompikumpi∙ cos θ
v_Oy = v_jompikumpi∙ Sen θ

Θ kulma, joka muodostaa alkuperäisen nopeuden vaakasuoraan nähden.

Se puolestaan matkapuhelimen alkuperäinen sijainti on koordinaattipiste (x_jompikumpi,ja_jompikumpi) tai vastaavasti, asetettu sijaintivektori:

r -_jompikumpi (t) = x_jompikumpi Yllyttää + ja_jompikumpi J -

Huomaa, että esitetyissä yhtälöissä negatiivinen merkki on osoitettu pystysuuntaiseen suuntaan, joten y (t) -yhtälön kolmas termi ottaa sen. On myös mahdollista määrittää alkuperä matkapuhelimen alkuperäiselle sijainnille.

Ammuksen välitön nopeus

Hetkellinen nopeus V (t) on ensimmäinen asennosta, kun suhteessa. Se lasketaan soveltamalla tunnettuja johdannaisääntöjä:

v(t) = R ' (t) = [x (t-A Yllyttää + ja(t-A J --'= x '(t-A Yllyttää + ja'(t-A J = v_härkäYllyttää + (V_Oy - Gt) J -

Nopeusmoduuli annetaan:

$\dpi110 \left|\textbfv \right|=\sqrtv_ox^2+v_oy^2$

Ammuksen välitön kiihtyvyys

On tiedossa, että se on G pystysuunnassa ja suunnassa alaspäin. Tämä todennetaan tietäen, että kiihtyvyys on ensimmäinen nopeuden johdannainen ajan suhteen (tai aseman toinen johdannainen ajan suhteen, jos se on suositeltava):

-lla(t) = V ' (t) = [V_härkäYllyttää + (V_Oy - Gt) J -] '= [V_härkäYllyttää] '+ [(v_Oy - Gt) J -] '= = - g J -

Tämä on juuri odotettu tulos.

Liikuntaa

Ottaen huomioon vektoritoiminto r - (t) = 3T Yllyttää + (T - 1) J -, löytö R '(t) ja r "(T).

Ratkaisu

Johdannaisääntöjen soveltaminen jokaiseen komponenttiin, sinulla on:

Voi palvella sinua: Integraatiovakio: Merkitys, laskenta ja esimerkit

R '(t) = = 3 Yllyttää + J -

Ja koska vakion johdannainen on 0-

r "(t) = 0 -

Tarkoittaen, r "(t) on yhtä suuri kuin nollavektori.

Viitteet

Figueroa, D. 2005. Sarja: Tieteen ja tekniikan fysiikka. Osa 1. Kinematiikka. Toimittanut Douglas Figueroa (USB).
Larson, r. Laskenta analyyttisellä geometrialla. Toinen. Painos. McGraw Hill.
MathOnline. Vektoriarvoiset toiminnot. Toipunut: MathOnline.Wikidot.com.
Aita. Laskensa tilavuus 3. Haettu osoitteesta: OpenStax.org.
Purcell, E. J -. 2007. Laskeminen. Pearson -koulutus.