Vapauden asteet kuinka laskea niitä, tyyppejä, esimerkkejä

Se vapauden asteet Tilastoissa on satunnaisen vektorin riippumattomien komponenttien lukumäärä. Jos vektorilla on n komponentit ja on p lineaariset yhtälöt, jotka yhdistävät sen komponentit, sitten vapausaste Se on N-P.

Käsite vapauden asteet Se esiintyy myös teoreettisessa mekaniikassa, jossa bruttotilassa ne vastaavat tilan ulottuvuutta, jossa hiukkasliikenteet liikkuvat, paitsi ligatuurien lukumäärä.

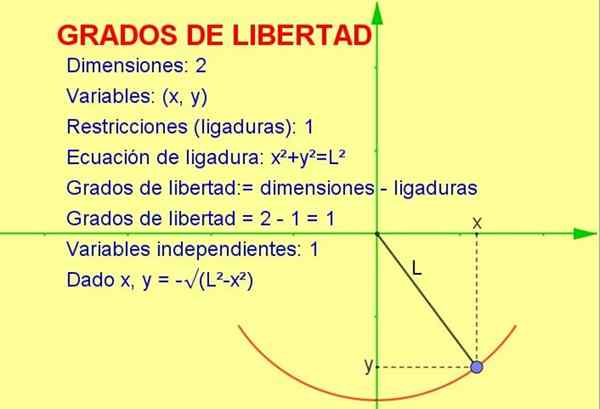
Kuvio 1. Heiluri liikkuu kahdessa ulottuvuudessa, mutta sillä on vain vapausaste, koska sen on pakko liikkua sädekaarissa L. Lähde: f. Zapata.

Tässä artikkelissa käsitellään tilastoihin sovellettavan vapausasteen käsitettä, mutta mekaaninen esimerkki on helpompi visualisoida geometrisellä tavalla.

[TOC]

Vapausasteen tyypit

Sen tilanteen mukaan tapa, jolla vapausasteiden lukumäärä laskee, voi vaihdella, mutta taustalla oleva idea on aina sama: kokonaismitat vähemmän rajoitusten lukumäärää.

Mekaanisessa tapauksessa

Harkitse hiukkasia, joka värähtelee köyteen (heiluri), joka liikkuu pystysuorassa tasossa X-Y (2 mittaa). Hiukkaset ovat kuitenkin velvollisia liikkumaan säteen ympärysmitalla, joka on yhtä suuri kuin köyden pituus.

Koska hiukkas voi liikkua vain kyseisellä käyrällä, niiden lukumäärä vapauden asteet Se on 1. Tämä voidaan visualisoida kuvassa 1.

Tapa laskea vapausasteiden lukumäärä on tehdä ero mittojen lukumäärässä paitsi rajoitusten lukumäärä:

Vapausasteet: = 2 (mitat) - 1 (ligaatio) = 1

Toinen selitys, jonka avulla voimme saavuttaa tuloksen, on seuraava:

-Tiedämme, että kaksi dimensionaalista sijaintia edustaa koordinaattipiste (x, y).

-Mutta kuten pisteen on täytettävä ympärysyhtälö (x² + ja² = L²) Muuttujan X tietylle arvolle muuttuja ja määritetään mainitulla yhtälöllä tai rajoituksella.

Tällä tavalla vain yksi muuttujista on riippumaton ja järjestelmässä Yksi (1) vapausaste.

Voi palvella sinua: Klassinen todennäköisyys: Laskenta, esimerkit, ratkaisut harjoitukset

Satunnaisten arvojen joukossa

Havainnollistaa, mitä käsite tarkoittaa, oletetaan, että vektori

x = (x₁, x₂,…, X_n-A

Edustaa näytettä n Satunnaiset arvot jakautuvat normaalisti. Tässä tapauksessa satunnainen vektori x haastaa n riippumattomat komponentit ja siksi sanotaan x haastaa n vapausasteet.

Rakennetaan vektori nyt r - jätteet

r - = (x₁ - , x₂ - ,.. ., x_n - -A

Missä se edustaa näytteen keskiarvoa, joka lasketaan seuraavasti:

= (x₁ + x₂ +.. .+ x_n) / n

Sitten summa

(x₁ - )+(x₂ - )+.. .+(x_n - ) = (x₁ + x₂ +.. .+ x_n) - n = 0

Se on yhtälö, joka edustaa rajoitusta (tai ligaatiota) vektorielementeissä r - jätteistä, koska jos N-1 tunnetaan, vektorikomponentit r -, Rajoitusyhtälö määrittää tuntemattoman komponentin.

Siksi vektori r - ulottuvuutta n rajoituksella:

∑ (x_Yllyttää - ) = 0

Haastaa (N - 1) vapausasteet.

Jälleen sovelletaan, että vapausasteiden lukumäärän laskeminen on:

Vapausasteet: = n (mitat) - 1 (rajoitukset) = n -1

Esimerkit

Varianssi ja vapausasteet

Varianssi s² Se määritellään datanäytteen poikkeamien (tai jätteiden) neliön keskiarvoksi:

s² = (r -Ollar -) / (N-1)

missä r - on jätevektori r - = (x1 -, x2 -, .. ., Xn -) ja paksu piste (Olla) on skalaarituotteen operaattori. Vaihtoehtoisesti varianssikaava voidaan kirjoittaa seuraavasti:

s² = ∑ (x_Yllyttää - -A² / (N-1)

Joka tapauksessa on huomattava, että laskettaessa jätteen neliön keskiarvoa se jaetaan (N-1) eikä n välillä, koska kuten edellisessä osassa on käsitelty, vapausasteiden lukumäärä vektori r - on (n-1).

Jos varianssin laskemiseksi se jaettiin välillä n (N-1) sijasta tuloksella olisi puolueellisuus, joka on erittäin merkittävä n alle 50.

Se voi palvella sinua: analyyttinen geometria

Kirjallisuudessa esiintyy myös kaava, joka on variaatio jakajan n (N-1) sijasta, kun kyse on populaation varianssista.

Mutta jätteen satunnaismuuttujan joukko, jota vektori edustaa r -, Vaikka siinä on ulottuvuus n, siinä on vain (N-1) vapausasteet. Jos tiedonumero on kuitenkin riittävän suuri (n> 500), molemmat kaavat lähentyvät samaan tulokseen.

Laskimet ja laskentataulukoita tarjoavat varianssin kaksi versiota ja keskihajontaa (joka on varianssin neliöjuuri).

Suosituksemme tässä esitetyn analyysin vuoksi on aina valita versio (N-1) joka kerta, kun on tarpeen laskea varianssi tai keskihajonta, tulosten välttämiseksi puolueellisuudella.

Chi -neliön jakautumisessa

Jotkut todennäköisyysjakaumat jatkuvassa satunnaismuuttujassa riippuvat parametrista, jota kutsutaan vapausaste, Näin on Chi -neliöjakauma (χ²-A.

Mainitun parametrin nimi tulee vain satunnaisen vektorin vapauden asteista, joihin tätä jakaumaa käytetään.

Oletetaan, että G -populaatioita on, joista N -koonäytteet otetaan:

X₁ = (x1₁, x1₂,... x1_n-A

X2 = (x2₁, x2₂,... x2_n-A

.. .

X_{J -} = (XJ₁, XJ₂,… XJ_n-A

.. .

Xg = (xg₁, Xg₂,… XG_n-A

Väestö J - sillä on keskimääräinen ja keskihajonta SJ, Seuraa normaalia jakautumista n (, SJ -A.

Tyypillinen tai normalisoitu muuttuja ZJ_Yllyttää on määritelty seuraavasti:

Zj_Yllyttää = (XJ_Yllyttää - ) / SJ.

Ja vektori Zj Se on määritelty näin:

Zj = (ZJ₁, Zj₂,…, ZJ_Yllyttää,…, ZJ_n) Ja noudata Normaalijakaumaa tyypillistä N (0,1).

Sitten muuttuja:

Q - = (Z1₁ ^2 + Z2₁^2+… . + Zg₁^2),… ., (Z1_n^2 + Z2_n^2+… . + Zg_n^2))

Seuraa jakaumaa χ²g) kutsutaan Chi -neliöjakauma vapausasteessa g.

Hypoteesin kontrastissa (ratkaistu esimerkki)

Kun haluat tehdä hypoteesin kontrastin tiettyjen satunnaisten tietojen perusteella, on tarpeen tuntea vapausasteiden lukumäärä g CHI -neliötestin soveltamiseksi.

Voi palvella sinua: jatkuva yhtenäinen jakauma: ominaisuudet, esimerkit, sovellukset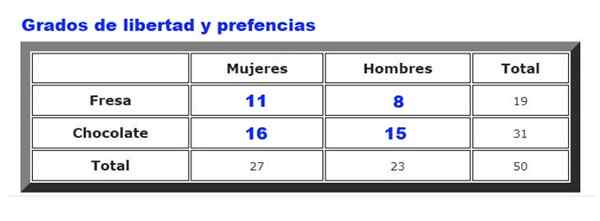 Kuva 2. Onko jäätelön maun ja asiakkaiden sukupuolen välillä suhdetta? Lähde: f. Zapata.

Esimerkiksi tietyn jäätelökaupan miesten ja naisten välillä kerätyt suklaa- tai mansikkajäätelöasetukset kerätyt tiedot analysoidaan. Tiheys, jolla miehet ja naiset valitsevat mansikkaa tai suklaata, on esitetty yhteenvetona kuvassa 2.

Ensinnäkin odotettu taajuustaulukko lasketaan, joka tehdään kertomalla Kokonaisrivit hänelle Kokonaispylväät, jaettuna Kokonaistiedot. Tulos on esitetty seuraavassa kuvassa:

Kuva 3. Odotettujen taajuuksien laskeminen havaittujen taajuuksien perusteella (siniset arvot kuvassa 2). Lähde: f. Zapata.

Sitten jatkamme Chi -neliön (tiedoista) seuraavalla kaavalla:

χ² = ∑ (f_jompikumpi - F_ja-A² / F_ja

Missä f_jompikumpi ovat havaitut taajuudet (kuva 2) ja f_ja ovat odotetut taajuudet (kuva 3). Summa on kaikissa riveissä ja sarakkeissa, jotka esimerkissämme antavat neljä termiä.

Kun olet tehnyt toiminnot, saat:

χ² = 0,2043.

Nyt on tarpeen verrata teoreettiseen neliöön, joka riippuu vapausasteiden lukumäärä g.

Meidän tapauksessamme tämä luku määritetään seuraavasti:

G = (#filas - 1) (#columnas - 1) = (2 - 1) (2 - 1) = 1 * 1 = 1.

Osoittautuu, että tämän esimerkin vapausasteiden lukumäärä on 1.

Jos haluat tarkistaa tai hylätä nollahypoteesin (H0: Maun ja sukupuolen välillä ei ole korrelaatiota), jonka merkitsevyystaso on 1%, teoreettinen Chi -neliö lasketaan vapausasteella g = 1.

Arvoa, joka tekee kertyneen taajuuden (1 - 0.01) = 0.99, se on 99%. Tämä arvo (joka voidaan saada taulukoista) on 6.636.

Kun teoreettinen chi ylittää lasketun, niin nollahypoteesi varmistetaan.

Eli kerättyjen tietojen kanssa muuttujien maun ja sukupuolen välillä ei ole suhdetta.

Viitteet

1. Minitab. Mitkä ovat vapauden asteet? Haettu: tuki.Minitab.com.
2. Moore, David. (2009) Sovelletut tilastotiedot. Antoni Bosch Editor.
3. Leigh, Jennifer. Kuinka laskea vapausasteet tilastollisissa malleissa. Toipunut: Geniolandia.com
4. Wikipedia. Vapausaste (tilastot). Palautettu: on.Wikipedia.com
5. Wikipedia. Vapauden aste (fyysinen). Palautettu: on.Wikipedia.com