Tiedot eivät ole ryhmiteltyjä esimerkkejä ja liikunta ratkaistu

Se Ryhmittelemättömät tiedot Ne ovat niitä, joita luokille ei ole vielä järjestetty tutkimuksesta. Kun se on hallittavissa oleva määrä tietoja, yleensä 20 tai vähemmän, ja tietoja on vähän, niitä voidaan käsitellä ryhmiteltynä ja poimia niistä arvokasta tietoa.

Ryhmää koskevat tiedot tulevat tutkimuksesta tai tutkimuksesta, joka tehdään niiden saamiseksi, ja siksi puuttuvat prosessointi. Katsotaanpa joitain esimerkkejä:

Kuvio 1. Ryhmätiedot tulevat suoraan mistä tahansa tutkimuksesta, eikä niitä ole luokiteltu. Lähde: Pxhere.

-Älyllisen kerroin CI -kokeen tulokset 20 satunnaisessa opiskelijassa yliopistosta. Saadut tiedot olivat seuraavat:

119, 109, 124, 119, 106, 112, 112, 112, 112, 109, 112, 124, 109, 109, 109, 106, 124, 112, 112 106

-Erittäin suositun kahvilan 20 työntekijän ikä:

24, 20, 22, 19, 18, 27, 25, 19, 27, 18, 21, 22, 23, 19, 22, 27, 29, 23, 20

-Kymmenen matematiikan luokan 10 opiskelijan keskimääräiset lopulliset huomautukset:

3,2; 3.1; 2,4; 4,0; 3,5; 3,0; 3,5; 3,8; 4.2; 4.9

[TOC]

Dataominaisuudet

On olemassa kolme tärkeää ominaisuutta, jotka karakterisoivat joukon tilastollisia tietoja ryhmiteltynä tai eivät, jotka ovat:

-Sijainti, mikä on tiettyjen arvojen ryhmiteltyjen tietojen taipumus.

-Hajonta, Osoitus siitä, kuinka hajaantuneita tai levitettyjä ovat tietyn arvon ympärillä olevat tiedot.

-Muoto, Se viittaa tietojen jakautumiseen, mikä voidaan nähdä, kun heistä kuvaa. Tietyn keskusarvon vasemmalla tai oikealla puolella on erittäin symmetrisiä ja myös puolueellisia käyriä.

Jokaiselle näistä ominaisuuksista on useita toimenpiteitä, jotka kuvaavat niitä. Saatuaan he antavat meille panoraaman tietokäyttäytymisestä:

-Eniten käytettyjen sijaintitoimenpiteet ovat aritmeettinen keskiarvo tai yksinkertaisesti keskimääräinen, mediaani ja muoti.

-Dispersiossa käytetään usein aluetta, varianssia ja keskihajontaa, mutta ne eivät ole ainoita dispersiomittauksia.

Voi palvella sinua: Homotecia

-Ja muodon määrittämiseksi keskiarvoa ja mediaania verrataan puolueellisuuteen, kuten pian nähdään.

Keskimääräisen, mediaanin ja muodin laskeminen

-Aritmeettinen keskiarvo, Tunnetaan myös nimellä keskimääräinen ja merkitty nimellä X, se lasketaan seuraavasti:

X = (x₁ + x₂ + x₃ +... x_n) / n

Missä x₁, x₂,.. . x_n, ovat tietoja ja n on niiden kokonaismäärä. Summan summioissa on:

Tässä hakemisto I edustaa tietoja 1, data 2, data 3 ja niin edelleen, kunnes se on ainoa, mikä on viimeinen.

-Mediaani Se on arvo, joka näkyy datan järjestetyn peräkkäin, joten sen saamiseksi on tarpeen tilata tiedot ensin.

Jos havaintojen lukumäärä on outoa, sarjan keskipisteen löytämisessä ei ole mitään ongelmaa, mutta jos meillä on tietopari, kahta keskusta haetaan ja keskiarvotetaan.

-Muoti Se on tietojoukossa havaittu yleisin arvo. Sitä ei aina ole, koska on mahdollista, että arvoa ei toisteta useammin kuin toinen. Siellä voi olla myös kaksi yhtä suurta taajuutta.

Toisin kuin kaksi edellistä mittaa, muotia voidaan käyttää laadullisen tiedon kanssa.

Katsotaanpa, kuinka nämä sijaintitoimenpiteet lasketaan esimerkillä:

Ratkaistu esimerkki

Oletetaan, että haluat määrittää aritmeettisen keskiarvon, mediaanin ja muodin alussa ehdotetussa esimerkissä: Kahvilan 20 työntekijän ikä:

24, 20, 22, 19, 18, 27, 25, 19, 27, 18, 21, 22, 23, 19, 22, 27, 29, 23, 20

Se puoli Se lasketaan yksinkertaisesti lisäämällä kaikki arvot ja jakamalla n = 20, mikä on tietojen kokonaismäärä. Tällä tavalla:

Voi palvella sinua: Suhteellisuussuhteet: Konsepti, esimerkit ja harjoitukset

X = (24 + 20 + 22 + 19 + 18 + 27+ 25 + 19 + 27 + 18 + 21 + 22 + 23 + 21+ 19 + 22 + 27+ 29 + 23+ 20) / 20 =

= 22.3 vuotta.

Löytää mediaani Tietojoukko on ensin tilata:

18, 18, 19, 19, 19, 20, 20, 21, 21, 22, 22, 22, 23, 23, 24, 25, 27, 27, 27, 29

Kuten pari tieto. Koska molemmat ovat 22, mediaani on 22 vuotta.

Lopuksi, muoti Se tosiasia, joka toistetaan eniten tai jonka taajuus on suurempi, on tämä 22 vuotta.

Alue, varianssi, keskihajonta ja puolueellisuus

Alue on yksinkertaisesti ero pääaineen ja vähiten datan välillä ja sallii niiden variaation arvostamisen nopeasti. Mutta lukuun ottamatta on muita dispersiotoimenpiteitä, jotka tarjoavat lisätietoja tiedon jakelusta.

Varianssi ja keskihajonta

Varianssi on merkitty S: ksi ja se lasketaan lausekkeella:

Sitä työskentelee usein kvaasirianssin kanssa varianssin sijasta, joka lasketaan samalla tavalla, jaettuna vain N-1: llä, sen sijaan, että toimisi n:

Koska varianssi on neliöiden summa, johtaa näyteyksikön neliöön. Esimerkiksi kahvilan työntekijöiden ikäryhmien tutkimuksessa varianssi tulee vuosien kuluessa².

Tulokset perustellusti tulkitsee perustellusti keskihajonta, kuten varianssin neliöjuuri tai myös vakio-kvasi-devisaatio, joka on kvaasivarianssin neliöjuuri:

Puolueellisuus

Se on vertailu keskimääräisen x: n ja mediaanin välillä:

-Kyllä Med = Media X: Tiedot ovat symmetrisiä.

-Kun x> med: puolueellinen oikealle.

-Ja jos x < Med: los datos sesgan hacia la izquierda.

Liikuntaa

Löydä keskimääräinen, mediaani, muoti, sijoitus, varianssi, keskihajonta ja puolueellisuus 20 opiskelijan henkisen kerrointutkimuksen tuloksille:

Voi palvella sinua: matemaattiset toiminnot

119, 109, 124, 119, 106, 112, 112, 112, 112, 109, 112, 124, 109, 109, 109, 106, 124, 112, 112, 106

Ratkaisu

Tilaamme tiedot, koska mediaani on tarpeen löytää.

106, 106, 106, 109, 109, 109, 109, 109, 112, 112, 112, 112, 112, 112, 119, 119, 124, 124, 124

Ja laitamme ne taulukkoon seuraavasti. Toinen sarake, jonka otsikko on "kertynyt", on vastaavien tietojen summa ja edelliset.

Tämä sarake löytää keskimääräisen helposti jakamalla viimeisen kertymisen datan kokonaismäärän välillä, kuten ”kertyneen” sarakkeen lopussa nähdään:

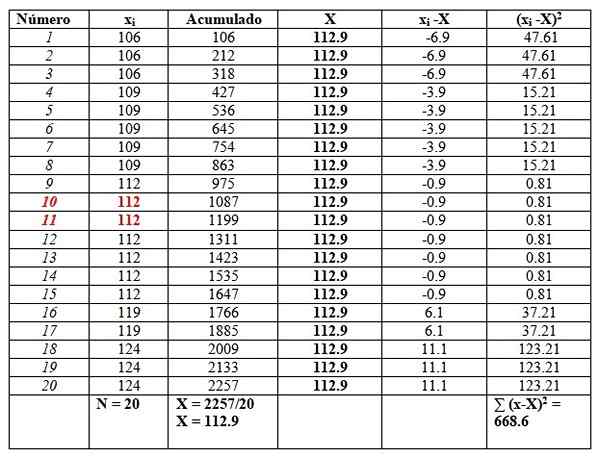
X = 112.9

Mediaani on punaisella korostettujen keskustietojen keskiarvo: numero 10 ja numero 11. Samoin kuin mediaani on 112.

Lopuksi, muoti on toistuvin arvo ja 112, 7 toistoa.

Dispersiotoimenpiteiden suhteen alue on:

124-106 = 18.

Varianssi saadaan jakamalla oikean sarakkeen lopullinen tulos n:

S = 668.6/20 = 33.42

Tässä tapauksessa keskihajonta on varianssin neliöjuuri: √33.42 = 5.8.

Toisaalta kvasivarianssin ja lähes standardipoikkeaman arvot ovat:

s_c= 668.6/19 = 35.2

Tavallinen kvasi-devisaatio = √35.2 = 5.9

Lopuksi, puolueellisuus on hieman oikealla, koska keskimäärin 112.9 on suurempi kuin mediaani 112.

Viitteet

1. Berenson, m. 1985. Hallinnon ja taloustieteen tilastot. Inter -American S.-Lla.
2. Canavos, G. 1988. Todennäköisyys ja tilastot: Sovellukset ja menetelmät. McGraw Hill.
3. DeVore, J. 2012. Tekniikan ja tieteen todennäköisyys ja tilastot. Kahdeksas. Painos. Kyynärmä.
4. Levin, r. 1988. Järjestelmänvalvojien tilastot. Toinen. Painos. Prentice Hall.
5. Walpole, r. 2007. Tekniikan ja tieteen todennäköisyys ja tilastot. Pearson.