Homokedisuus Mikä on, merkitys ja esimerkit

Se Homosedia Ennustavassa tilastollisessa mallissa se tapahtuu, jos yhden tai useamman havainnon kaikissa tietoryhmissä mallin varianssi selittävien (tai riippumattomien) muuttujien suhteen pysyy vakiona.

Regressiomalli voi olla homocedastinen tai ei, jolloin puhumme heterokoteus.

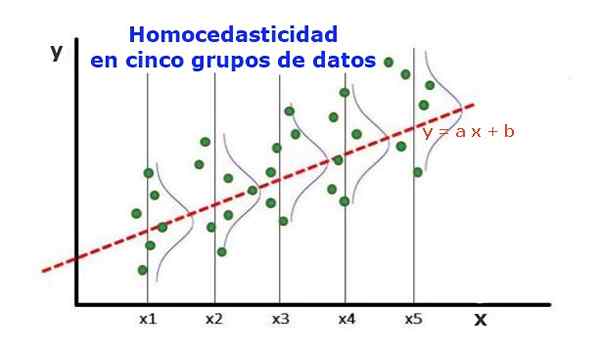
Kuvio 1. Viisi dataryhmää ja sarjan regression säätö. Ennustetun arvon varianssi on sama kussakin ryhmässä. (UPAV-kirjasto.org)

Useiden riippumattomien muuttujien tilastollista regressiomallia kutsutaan homocedaticiksi, vain jos ennustetun muuttujan virheen (tai riippuvaisen muuttujan keskihajonta) varianssi pysyy yhtenäisenä selittävien tai riippumattomien muuttujien eri ryhmille.

Kuvion 1 viidessä tietoryhmässä varianssi on laskettu kussakin ryhmässä suhteessa regression arvioiman arvoon, kääntäen samat kussakin ryhmässä. Oletetaan myös, että tiedot seuraavat normaalia jakaumaa.

Graafisella tasolla se tarkoittaa, että pisteet ovat tasaisesti dispergoituneet tai hajallaan ennustetun arvon ympärille regression säätöllä ja että regressiomallilla on sama virhe ja pätevyys selittävän muuttujan alueelle.

[TOC]

Homosedian merkitys

Homoksadastisuuden merkityksen havainnollistamiseksi ennusttilastoissa on välttämätöntä kontrastia vastakkaisen ilmiön, heterokedisuuden kanssa.

Homocedastiikka verrattuna heterokesitykseen

Kuvan 1 tapauksessa, jossa on homosediaa, on täytettävä, että:

Var ((y1-y1); x1) ≈ var ((y2-y2); x2) ≈ ... var (y4-y4); x4)

Jos Var ((Yi-II); xi) edustaa varianssia, pari (xi, yi) edustaa ryhmän I tosiasiaa, kun taas Yi on arvo, joka ennustaa ryhmän keskimääräisen XI-arvon regression. Ryhmän I tietojen varianssi lasketaan seuraavasti:

Var ((yi -ii); xi) = ∑j (yij - yi)^2/n

Päinvastoin, kun heterosedia tapahtuu, regressiomalli ei välttämättä ole voimassa koko alueelle, jolla se laskettiin. Kuvio 2 näyttää esimerkin tästä tilanteesta.

Voi palvella sinua: mitkä ovat sisäiset vaihtoehtoiset kulmat? (Harjoituksilla)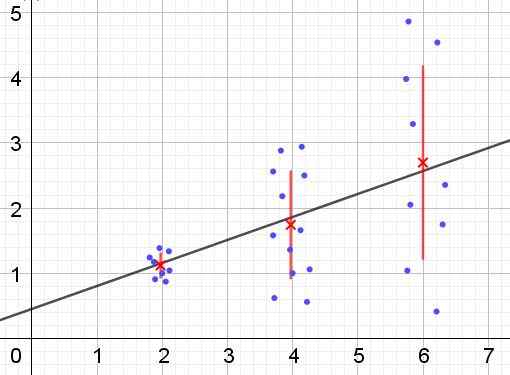 Kuva 2. Dataryhmä, jolla on heterokedisuus. (Oma yksityiskohta)

Kuviossa 2 kolme dataryhmää ja sarjan joukkoa esitetään lineaarisella regressiolla. On huomattava, että toisen ja kolmannen ryhmän tiedot ovat hajallaan kuin ensimmäisessä ryhmässä. Kuvion 2 kaavio näyttää myös kunkin ryhmän ja sen virhepalkin ± σ keskiarvon, joka on kunkin dataryhmän σ -keskihajonta. On muistettava, että keskihajonta σ on varianssin neliöjuuri.

On selvää, että heterokotiikan tapauksessa regression estimoinnin virhe muuttuu selittävän tai riippumattoman muuttujan arvoalueilla ja väliajoissa, joilla tämä virhe on erittäin suuri, regression ennuste on epäluotettava tai ei sovellettavissa.

Regressiomallissa virheet tai jätteet (y -y) on jaettava yhtäläisellä varianssilla (σ^2) riippumattomien muuttujien arvojen ajanjaksolla. Tästä syystä hyvän regressiomallin (lineaarinen tai epälineaarinen) on läpäistävä homocedasticity testi. 

Homokedisuustestit

Kuviossa 3 esitetyt kohdat vastaavat tutkimuksen tietoja, joissa etsitään talojen hintojen (dollareissa) välistä suhdetta neliömetrien koosta tai pinta -alasta riippuen.

Ensimmäinen harjoittelumalli on lineaarinen regressio. Ensinnäkin on huomattava, että säädön määrityskerroin r^2 on melko korkea (91%), joten voidaan ajatella, että säätö on tyydyttävä.

Kaksi aluetta voidaan kuitenkin erottaa selvästi säätökaaviosta. Yksi heistä, oikealla olevassa ovaisessa lukittuna, kohtaa homocedastisuuden, kun taas vasemman alueen ei ole homocedastiikkaa.

Voi palvella sinua: polynomin luokka: miten se määritetään, esimerkkejä ja harjoituksia

Tämä tarkoittaa, että regressiomallin ennustaminen on riittävä ja luotettava välillä 1800 m^2 - 4800 m^2, mutta erittäin riittämätön tämän alueen ulkopuolella. Heterotedisella alueella virhe ei ole vain erittäin suuri, vaan myös tiedot näyttävät seuraavan toista trendiä, jotka ovat erilaisia ​​kuin lineaarisen regressiomallin ehdottama.

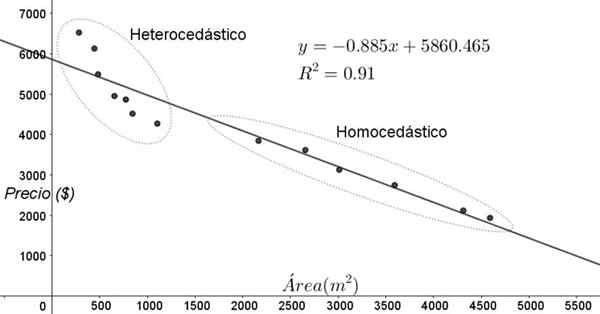Kuva 3. Asuntojen hinnat vs. pinta -ala ja ennustava malli lineaarisella regressiolla, joka osoittaa homocedaticity- ja heterosedia -alueita. (Oma yksityiskohta)

Tietojen dispersiokaavio on yksinkertaisin ja visuaalinen testi niiden homocedaticylle, mutta joskus se ei ole niin ilmeinen kuin kuvassa 3 esitetyssä esimerkissä, on tarpeen turvautua apumuuttujien grafiikoihin, jotka.

Standardisoidut muuttujat

Otetaan käyttöön tarkoituksena, jolla homosedastiikka on saavutettu ja jossa ei ole, standardisoidut muuttujat ZRE: t ja Zreded otetaan käyttöön:

Zres = abs (y - y)/σ

Zpred = y/σ

On huomattava, että nämä muuttujat riippuvat käytetystä regressiomallista, koska se on regression ennustamisen arvo. Alla on ZRES vs zred -dispersiokaavio samasta esimerkistä:

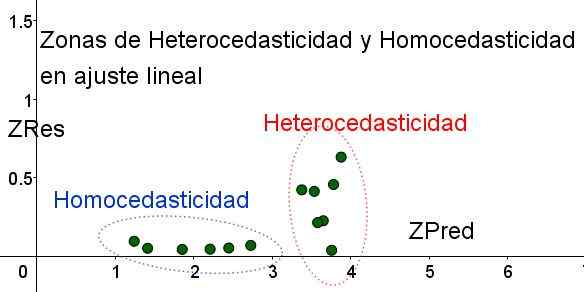Kuva 4. On huomattava, että homocedasticity -vyöhykkeellä ZRES on edelleen tasainen ja pieni ennustealueella (oma yksityiskohta).

Kuvion 4 kaaviossa standardisoitujen muuttujien kanssa alue, jolla jäännösvirhe on pieni ja tasainen on selvästi erotettu, suhteessa siihen, joka ei. Ensimmäisellä alueella homocedaticity toteutetaan, kun taas jäännösvirhe on hyvin muuttuva ja suuri.

Regression säätöä sovelletaan samaan dataryhmään 3. Tulos on esitetty seuraavassa kuvassa:

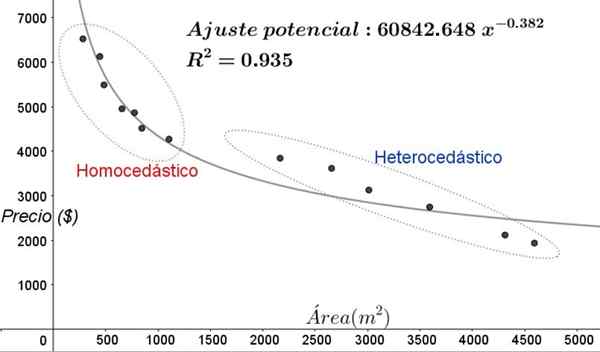Kuva 5. Uudet homosedastisuus- ja heterokesitysalueet datan säätämisessä ei-lineaalisen regressiomallin avulla. (Oma yksityiskohta).

Kuvion 5 kaaviossa homokediset ja heterokoostiset alueet tulisi selvästi huomata. On myös huomattava, että nämä alueet vaihdettiin suhteessa lineaariseen säätömalliin muodostettuihin suhteisiin.

Voi palvella sinua: kulmat, ominaisuudet ja esimerkit

Kuvion 5 kaaviossa on selvää, että jopa silloin, kun säätö määritetään melko korkea (93,5%), malli ei sovellu selittävän muuttujan koko ajanjaksoon, koska vanhemmille arvoille annetut tiedot M^2: lla on heterocedaticity.

Ei -tietoiset homocedasticity testit

Yksi eniten käytettyjä ei -tietoisia testejä varmistaa, onko homocedaticisuus täytettävä vai ei Breusch-Pagan-testi.

Kaikkia tämän testin yksityiskohtia ei anneta tässä artikkelissa, vaan sen perusominaisuudet ja saman vaiheet on laajalti hahmoteltu:

1. Regressiomallia sovelletaan n dataan ja saman varianssi lasketaan suhteessa mallin σ^2 = ∑j (yj - y)^2/n arvoon liittyvään arvoon.
2. Uusi muuttuja ε = (yj - y)^2) / (σ^2) määritetään
3. Sama regressiomallia käytetään uuteen muuttujaan ja sen uudet regressioparametrit lasketaan.
4. Chi -neliökriittinen arvo (χ^2) määritetään, tämä on puolet neliöiden uuden jätteen summasta ε -muuttujassa.
5. CHI -neliötaulua käytetään ottaen huomioon X -akselin (yleensä 5%) merkitsevyystaso ja vapausasteiden lukumäärä (#OF -regressiomuuttujat paitsi yksikkö), jotta saadaan levyn arvo.
6. Vaiheessa 3 saatua kriittistä arvoa verrataan taulukossa havaittuun arvoon (χ^2).
7. Jos kriittinen arvo on alle taulukon, sinulla on nollahypoteesi: Homokedisuus on
8. Jos kriittinen arvo on taulukon yläpuolella, sinulla on vaihtoehtoinen hypoteesi: Homocedastiikkaa ei ole.

Suurin osa tilastollisista tietokonepaketeista, kuten: SPSS, Minitab, R, Python Panda, SAS, Statgraphic ja Useat muut sisältävät homocedasticity testi Breusch-Pagan. Toinen testi varianssin yhtenäisyyden varmistamiseksi Levene -testi.

Viitteet

1. Laatikko, metsästäjä ja metsästäjä. (1988) Tilastot tutkijoille. Käännyin toimittajat.
2. Johnston, J (1989). Econometriikan menetelmät, Vicens -Ives -toimittaja.
3. Murillo ja González (2000). Economety -käsikirja. Las Palmas de Gran Canaria. Haettu osoitteesta: ULPGC.On.
4. Wikipedia. Homosedia. Palautettu: on.Wikipedia.com
5. Wikipedia. Homoskedatiivisuus. Haettu: vuonna.Wikipedia.com