Empiirinen sääntö, miten sitä sovelletaan, mihin se on, harjoitukset ratkaistu

Eräs Empiirinen sääntö Se on seurausta käytännön kokemuksesta ja tosielämän havainnosta. Voit esimerkiksi tietää, että lintulajeja voidaan havaita tietyissä paikoissa kunkin vuoden aikana ja että havainnot voidaan vahvistaa "sääntö", joka kuvaa näiden lintujen elinkaaria.

Tilastoissa empiirinen sääntö viittaa havaintojen ryhmittelymuotoon keskimääräisen tai keskimääräisen tai keskimääräisen poikkeaman yksiköiden ympärillä.

Oletetaan, että sinulla on joukko ihmisiä, joiden keskimääräinen korkeus on 1.62 metriä ja keskihajonta 0.25 metriä, sitten empiirinen sääntö mahdollistaisi esimerkiksi kuinka monta ihmistä olisi keskimäärin enemmän tai vähemmän keskihajonta?

Sääntöjen mukaan 68% tiedoista on enemmän tai vähemmän keskimääräistä keskimääräistä poikkeamaa, ts. 68 prosentilla ryhmästä ihmisillä on korkeus välillä 1.37 (1.62-0.25) ja 1.87 (1.62+0.25) metriä.

[TOC]

Mistä empiirinen sääntö tulee?

Empiirinen sääntö on yleistävä Tchebyshevin lause ja normaali jakauma.

Tchebyshev -lause

Tchebyshevin lause sanoo, että: joillekin arvoille k> 1, todennäköisyys, että satunnaismuuttuja on keskiarvojen joukossa, joka on keskiarvo, joka on keskihajonta ja keskimäärin enemmän k -kertaa, keskihajonta on suurempi tai yhtä suuri kuin (1 -1 /k²-A.

Tämän lauseen etuna on, että sitä sovelletaan erillisiin tai jatkuviin satunnaismuuttujiin, joilla on todennäköisyysjakauma, mutta siitä määritetty sääntö ei ole aina kovin tarkka, koska se riippuu jakauman symmetriasta. Mitä epäsymmetrisempi satunnaismuuttujan jakauma, vähemmän sopeutettu sääntöön on sen käyttäytyminen.

Tästä lauseesta määritelty empiirinen sääntö on:

Jos k = √2, sanotaan, että 50% tiedoista on aikavälillä: [µ - √2 s, µ + √2 s]

Jos k = 2, sanotaan, että 75% tiedoista on aikavälillä: [µ - 2 s, µ + 2 s]

Jos k = 3, sanotaan, että 89% tiedoista on aikavälillä: [µ - 3 s, µ + 3 s]

Normaalijakauma

Normaali jakauma tai Gauss Bell mahdollistaa empiirisen säännön tai säännön 68 - 95 - 99 määrittämisen.7.

Voi palvella sinua: osuus

Sääntö perustuu satunnaismuuttujan todennäköisyyksiin keskimäärin pienempien, kahden tai kolmen standardipoikkeaman ja keskimäärin yhden, kahden tai kolmen standardipoikkeaman välillä väliajoin.

Empiirinen sääntö määrittelee seuraavat aikavälit:

68.27% tiedoista on aikavälillä: [µ - s, µ + s]

95.45% tiedoista on aikavälillä: [µ - 2s, µ + 2s]

99.73% tiedoista on aikavälillä: [µ - 3S, µ + 3S]

Kuvassa voit nähdä, kuinka nämä välit esitetään ja niiden välinen suhde lisäämällä graafisen pohjan leveyttä.

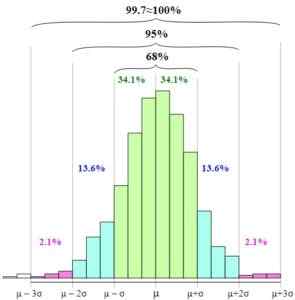Empiirinen sääntö. MELIKAMP [CC BY-SA 4.0 (https: // creativecommons.org/)] satunnaismuuttujan standardointi, ts. Satunnaismuuttujan ekspressio standardin tai normaalin muuttujan suhteen, yksinkertaistaa empiirisen säännön käyttöä, koska muuttujan Z on keskimäärin yhtä suuri kuin nolla ja keskihajonta tasa -arvoinen yhdelle.

Siksi tavanomaisen normaalin muuttujan z -asteikon empiirisen säännön soveltaminen määrittelee seuraavat aikavälit:

68.27% tiedoista on aikavälillä: [-1, 1]

95.45% tiedoista on aikavälillä: [-2, 2]

99.73% tiedoista on aikavälillä: [-3, 3]

Kuinka soveltaa empiiristä sääntöä?

Empiirinen sääntö antaa sinun lyhentää laskelmia normaalijakauman kanssa.

Oletetaan, että 100 yliopisto -opiskelijan ryhmän keski -ikä on 23 vuotta, ja keskihajonta on 2 vuotta. Mitä tietoja empiirinen sääntö sallii?

Empiirisen säännön soveltaminen viittaa vaiheiden seurauksena:

1- Rakenna sääntövälejä

Koska keskiarvo on 23 ja keskihajonta on 2, niin välit ovat:

[µ - s, µ + s] = [23 - 2, 23 + 2] = [21, 25]

[µ - 2s, µ + 2s] = [23 - 2 (2), 23 + 2 (2)] = [19, 27]

[µ - 3S, µ + 3S] = [23 - 3 (2), 23 + 3 (2)] = [17, 29]

2- Laske opiskelijoiden lukumäärä kussakin aikavälillä prosenttimäärien mukaan

(100)*68.27% = 68 opiskelijaa suunnilleen

(100)*95.45% = noin 95 opiskelijaa

(100)*99.73% = 100 opiskelijaa

3- Ikävälillä liittyy opiskelijoiden määriä ja tulkittu

Ainakin 68 opiskelijaa on 21-25 -vuotiaita.

Voi palvella sinua: Kuvailevat tilastot: historia, ominaisuudet, esimerkit, käsitteet

Ainakin 95 opiskelijaa on 19–27 -vuotiaita.

Lähes 100 opiskelijaa on 17–29 vuotta vanhoja.

Mikä on empiirinen sääntö?

Empiirinen sääntö on nopea ja käytännöllinen tapa analysoida tilastotietoja, ja se on yhä luotettavampi siinä määrin, että jakauma on lähellä symmetriaa.

Sen hyödyllisyys riippuu kentästä, jolla sitä käytetään ja nousevista kysymyksistä. On erittäin hyödyllistä tietää, että kolmen standardipoikkeaman arvojen esiintyminen on melkein epätodennäköistä alle keskimääräistä, jopa ei -normaalien jakautumismuuttujien, vähintään 88.8% tapauksista on kolmella sigmavälillä.

Yhteiskuntatieteissä yleisesti vakuuttava tulos on keskimäärin enemmän tai vähemmän kahden sigman (95%) väliaika, kun taas hiukkasfysiikassa uusi vaikutus vaatii viisi Sigmas -aikaväliä (99.99994%), jota pidetään löytönä.

Ratkaisut

Kanit varannossa

Villieläinten varannossa arvioidaan, että keskimäärin 16.000 kania, joiden keskihajonta on 500 kanin. Jos muuttujan "kanien lukumäärä varannossa" ei tunneta, onko se mahdollista.000 ja 17.000 kani?

Väli voidaan esitellä näillä termeillä:

15000 = 16000 - 1000 = 16000 - 2 (500) = µ - 2 s

17000 = 16000 + 1000 = 16000 + 2 (500) = µ + 2 s

Siksi: [15000, 17000] = [µ - 2 s, µ + 2 s]

Tchebyshevin lauseen soveltamisessa on todennäköisyys, että se on vähintään 0.75, että villieläinvarannon kanien väestö on välillä 15.000 ja 17.000 kani.

Maasta lasten keskiarvot

Yhden vuoden ikäisten lasten keskimääräinen paino on yleensä jakautunut keskimäärin 10 kilogrammilla ja keskihajonnalla noin 1 kiloa.

a) Arvioi maan yhden vuoden lasten prosenttiosuus, joiden keskimääräinen paino on välillä 8–12 kiloa.

8 = 10 - 2 = 10 - 2 (1) = µ - 2 s

12 = 10 + 2 = 10 + 2 (1) = µ + 2 s

Siksi: [8, 12] = [µ - 2s, µ + 2s]

Se voi palvella sinua: Tukey -testi: Mikä on esimerkiksi ratkaistu harjoitus

Empiirisen säännön mukaan voidaan vahvistaa, että 68.27 prosentilla maan lapsista on 8–12 kiloa painoa.

b) Mikä on todennäköisyys löytää yhden vuoden ikäinen lapsi, jonka paino on vähintään 7 kiloa?

7 = 10 - 3 = 10 - 3 (1) = µ - 3 s

On tiedossa, että 7 kilogrammaa painoa edustaa arvoa µ - 3S, samoin kuin tiedetään, että 99.73% lapsista on 7–13 kiloa painoa. Se jättää vain 0.27% kaikista äärimmäisistä lapsista. Puolet heistä, 0.135%: lla on 7 kilogrammaa painoa tai vähemmän ja toinen puoli, 0.135%, on 11 kiloa painoa tai enemmän.

Joten voidaan päätellä, että todennäköisyys on 0.00135, että lapsella on 7 kiloa painoa tai vähemmän.

c) Jos maan väestö saavuttaa 50 miljoonaa asukasta ja yhden vuoden lapsia?

9 = 10 - 1 = µ - S

11 = 10 + 1 = µ + S

Siksi: [9, 11] = [µ - s, µ + s]

Empiirisen säännön mukaan 68.27% yhden vuoden ikäisistä lapsista on aikavälillä [µ -s, µ + s]

Maassa on 500 000 vuotta vuodessa (1% 50 miljoonasta), joten 341350 lasta (68.27% 500000: sta) on välillä 9–11 kiloa painoa.

Viitteet

1. Abraira, V. (2002). Vakiopoikkeama ja vakiovirhe. Semergen -aikakauslehti. Verkko palautettu.Arkisto.org.
2. Freund, r.; Wilson, W.; Mohr, D. (2010). Tilastolliset menetelmät. Kolmas Ed. Akateeminen lehdistösekki Inc.
3. Alicante Server (2017). Empiirinen sääntö (tilastolliset ehdot). Sanasto toipui.palvelin-.com.
4. Lind, D.; Marchal, W.; Wathen, S. (2012). Tilastot sovelletaan liiketoimintaan ja talouteen. Kymmenes ED. McGraw-Hill/Amerikanvälinen Meksikosta. -Lla.
5. Salinas, H. (2010). Tilastot ja todennäköisyydet. Toipunut UDA: sta.Cl.
6. Sokal, r.; Rohlf, f. (2009). Johdanto biostatistiikkaan. Toinen ED. Dover Publications, Inc.
7. Spiegel, M. (1976). Todennäköisyys ja tilastot. Schaum -sarja. McGraw-Hill/Amerikanvälinen Meksikosta. -Lla.
8. Spiegel, M.; Stephens, L. (2008). Tilastot. Neljäs Ed. McGraw-Hill/Amerikanvälinen Meksikosta. -Lla.
9. Stat119 Review (2019). Empiirinen ratkaisusääntökysymykset. Haettu Stat1199Review.com.
10. (2019). 68-95-99.7 sääntö. Haettu jstk.Wikipedia.org.