Matematiikka

Negatiivinen homotecia

Negatiivinen homotecia
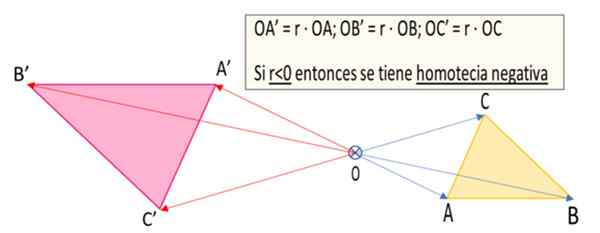
Kuvio 1. Kolmio A'b'c 'on ABC -kolmion homotetinen muunnos pisteeseen tai negatiivisen homotecia r = -1: n syynä.5 (valmistettu: f zapata).

Mikä on negatiivinen homotecia?

Negatiivinen homotecia on muuntaminen, jossa tasossa sisältävän monikulmion on kuvassa toinen monikulmio samassa tasossa, yhtä suuret kulmat ja vastaavien puolten kanssa verrannollinen alkuperäisen sivuihin. Kun homotecia on negatiivinen, kuvaa pyöritetään puoli kierrosta alkuperäisen kuvan suhteen.

Homotecialle on ominaista Homotecia -keskus JOMPIKUMPI ja suhteellisuusvakio, jota kutsutaan syyksi r -. Kun r - Se on negatiivinen luku, joten puhutaan negatiivisesta homoteciasta.

Kuinka homotecia -muutos tehdään?

Selitetään, kuinka negatiivinen homotecia suoritetaan, otamme kuvan 1, jossa kolmio on ABC Kuka haluaa rakentaa negatiivisen homotettinsa.

1.- Se alkaa valita homotecia -keskuksen, mikä on tämä tapaus JOMPIKUMPI.

2.- -Sta JOMPIKUMPI Suuntautuneet segmentit on rakennettu (vektorit) OA, Ob ja Oc jotka menevät Homotecian keskustasta jokaiseen kolmion kärkipisteeseen.

3.- Homotecia -syy valitaan r -. Kuten haluat negatiivisen homotecian, sitten r - Sen on oltava vähemmän kuin nolla. Kuvan 1 tapauksessa se otettiin R = -1.5.

4.- Vektorit vedetään Oa ', Ob ' ja Oc ', jotka ovat vastaavasti Oa '= r ∙ OA, Ob '= r ∙ OB  ja OC '= R ∙ OC. Kuten R = -1.5, Se on negatiivinen luku, sitten vektorit Oa ', Ob ' ja Oc ' Heillä on suunta vastaavien kollegojensa kanssa OA, Ob ja Oc. Mutta järjen absoluuttisena arvona r - On | R | = 1.5 koot Oa ', Ob'ja Oc ' Ne ovat kerran ja puoli suurempia kuin heidän kollegansa OA, Ob ja Oc.

5.- Vektorien vinkit Oa ', Ob ' ja Oc ' Määritä kolmion kärkipisteet A'b'c ' Mikä on kolmion negatiivinen homotetiikka ABC.

Negatiivisen homotecian ominaisuudet

Se negatiivinen homotecia, kutsutaan myös Käänteinen homotecia, Sillä on seuraavat ominaisuudet:

Se voi palvella sinua: Monilaitteet 8: mitä ovat ja selitys

1.- Kuvan monikulmion ja alkuperäisen monikulmion välisillä vastaavilla puolilla on suhteelliset pituudet, mikä on suhteellisuusvakio. Homotecia -suhteen absoluuttinen arvo, toisin sanoen kuva on monistettu tekijässä | r | niin kauan kuin | r | on suurempi kuin yksikkö, mutta kuva vähenee, jos | r | on vähemmän kuin yksikkö.

2.- Kuvan vastaavien sivujen ja alkuperäisen kuvan välisillä kulmilla on samat mitat.

3.- Alkuperäisen ja kuvan väliset homologiset sivut ovat yhdensuuntaiset toistensa kanssa.

4.- Vastaavat segmentit negatiivisen homotecian tapauksessa ovat yhdensuuntaiset, mutta ohjeiden tai vastakkaisen suuntaan. Esimerkiksi kuviossa 1 segmentin AB: n homologinen A'B 'on yhdensuuntainen ensimmäisen kanssa, mutta vastakkaiseen suuntaan.

Vertailu positiiviseen homoteciaan

Sitä kutsutaan positiiviseksi homoteciaksi, jossa homotecia -suhde on positiivinen lukumäärä. Positiivisen homotecian rakentamiseksi noudatetaan samoja vaiheita kuin negatiivinen homotecia:

1.- Valitse Homotecia -keskus, meidän tapauksessamme JOMPIKUMPI (Katso kuva 2).

2.- Piirrä suuntautuneet segmentit (vektorit), jotka vaihtelevat homotecian keskustasta monikulmion kärkipisteisiin, kuvion 2 tapauksessa nämä ovat: OA, Ob ja Oc.

3.- Valitse homotecia -suhde, joka on positiivinen luku, esimerkiksi kuvion 2 tapauksessa se on valittu R = 0.5.

4.- Vektorit vedetään Oa ', Ob ' ja Oc ', jotka ovat vastaavasti Oa '= r ∙ OA, Ob '= r ∙ OB ja OC '= R ∙ OC. Kuten r - Se on positiivinen luku, sitten vektorit Oa ', Ob ' ja Oc ' Heillä on sama osoite kuin OA, Ob ja Oc. Pituudet Oa ', Ob'ja Oc ' He ovat puolet siitä, että heidän kollegansa OA, Ob ja Oc, Koska syy on R = 0.5.

5.- Lopuksi A'b'c '-siirtoihin liittyy Homotetisen kolmion saamiseksi ABC: lle syystä 1/2.

Voi palvella sinua: nelikulmainen: elementit, ominaisuudet, luokittelu, esimerkit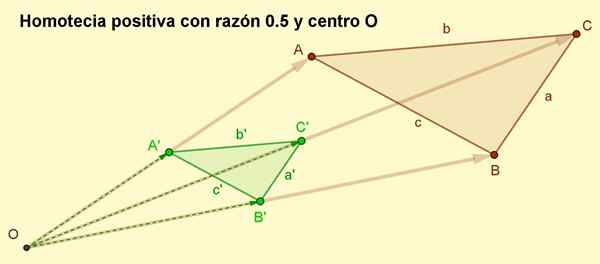 Kuva 2. Positiivinen homotecia perustellusti 0,5 ABC -kolmion tuloksista. Positiivisessa homoteciassa suuntautuminen ylläpidetään. (Valmistaja: f. Zapata)

Homotecia -esimerkkejä

Homotecia esiintyy eri tilanteissa:

Elokuvaprojektorit

Elokuvaprojektorissa kehykseen tallennettu kuva projisoidaan ja laajenee näytölle, ja jotta voidaan nähdä, että kehys sijoitetaan oikealle, koska Homotecia -keskus on linssin keskellä Projektorin linssin linssi kehyksen ja näytön välillä (negatiivinen homotecia, katso kuva 3)

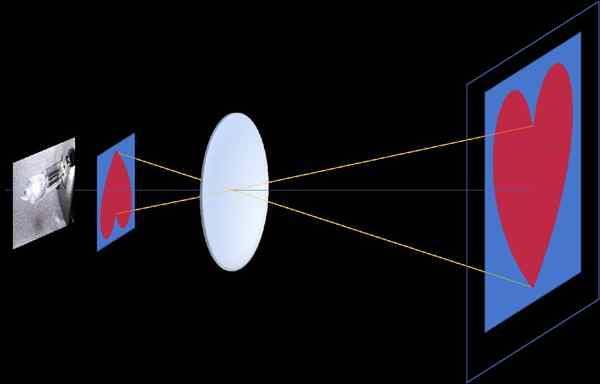Kuva 3. Negatiivinen homotecia esiintyy elokuvaprojektorissa, joka on tallennettu läpikuultavaan kehykseen ja näytölle projisoidun kuvan välillä. Homotecia -keskus on linssin optisessa keskuksessa, joka puolestaan ​​sijaitsee kehyksen ja näytön välissä. Lähde: f. Zapata.

Valokuvakamerat

Tämä periaate koskee myös kameroita: Valokuvan valoa, joka sijaitsee tietyllä etäisyydellä linssistä, projisoidaan valokuva -anturille, joka voi olla kevyt herkkä kemiallinen kalvo tai CCD -anturi, jos se on digitaalikamera.

Anturissa tallennettu kuva on käännetty suhteessa todelliseen ja on yleensä suhteellisesti vähemmän kuin hän.

Käytännöllinen soveltaminen

Auringon ei pitäisi näyttää suoraan, koska se aiheuttaa pysyviä vaurioita verkkokalvolle, mutta sitä on kaksi mahdollisuutta tutkia: käytä suodattimia, jotka heikentävät valon voimakkuutta tai projisoivat sen kuvan näytöllä.

Voi palvella sinua: suhteellinen variaatio

Projektiolaite koostuu pituusputkesta d -d. Yksi putken päistä on peitetty alumiinifoliolla ja poraa sen keskellä nastalla. Toinen pää, joka toimii näytönä, on peitetty läpikuultavalla paperilla, joka voi olla sipulipaperi tai albaneenipaperi (vihannespaperi).

Harjoittele

Määritä auringon halkaisija, tietäen, että maanpäällisen kiertoradan säde on 150 miljoonaa kilometriä, että projisointiputki, kuten kuviossa 4 esitetty, on 2,2 metriä pitkä ja että projisoitu kuva on 2, 1 cm halkaisija.

Kuva 4. Putkessa aurinkolevyjen projisointiin negatiivinen homotecia -suhde tapahtuu. Lähde: f. Zapata.

Ratkaisu

Tiedot ovat seuraavat:

  • Putken pituus: D = 2,2 metriä
  • Sunin projisoitu kuvan halkaisija: S = 2,1 cm
  • Etäisyys aurinkoputkesta: r = 150 x 10^9 m
  • Todellinen auringon halkaisija: S = ¿?

Auringon halkaisijan saamiseksi käytetään suhteellisuussuhdetta homotecian suhteellisuuden mukaan (katso kuva 4):

Etäisyys aurinkoon on putken pituudella, koska auringon halkaisija on projisoidun kuvan halkaisija:

(R / d) = (s / s)

Tämän tasa -arvon puhdistaminen, että auringon todellinen halkaisija on projisoinnin halkaisija, kerrottuna osamäärällä auringon etäisyyden ja putken pituuden välillä:

S = s (r / d)

Numeeristen arvojen sijoittaminen on:

S = 2,1 x 10-2 M (150 x 109 m / 2,2 m)

S = 1,43 x 109 m.

Tämä tulos tulkitaan seuraavasti: auringon todellinen halkaisija on 1,43 miljoonaa kilometriä.

Viitteet

  1. Álvaro Rendón,. R -. 2004. Tekninen piirustus: Aktiviteettikirja.
  2. Antonio Álvarez de la Rosa, J. Lens. 2002. Affiniteetti, homologia ja homotecia.
  3. Baer, ​​r. 2012. Lineaarinen algebra ja projektiivinen geometria. Couer Corporation.
  4. Hebert, ja. 1980. Yleinen matematiikka, todennäköisyys ja tilastot.
  5. Messerve, b. JA. 2014. Geometrian peruskäsitteet. Couer Corporation