Taustan ja kehityksen geometrian historiasta sen alkuperästä

Se Geometrian historia Se alkaa ensimmäisistä sivilisaatioista, jotka käyttivät tätä matematiikan haaraa käytännöllisellä tavalla, erityisesti Indo Valleyn ja Babylonin kansat, jotka tunsivat putouskolmiot, noin 3000 toiseen.C.

Egyptin kirjoituksen kirjoituksissa (1550.C.) Menetelmiä käytetään ympyrän pinta -alan laskemiseen. Babylonialaisilla oli puolestaan ​​yleisiä sääntöjä määrien ja alueiden mittaamiseksi. 

Ahme Papyrus tai Rhind Mathematical Papyrus

Sekä sivilisaatiot, egyptiläiset että babylonialaiset, tunsivat Pythagoras -lauseen versiot 1500 vuotta ennen Pythagoran versioita. Toisaalta vedalaisen ajan intialaiset (1500-100.C.) käytetty geometria alttarien rakentamisessa.

[TOC]

Muinainen Kreikka

Kreikkalaiset olivat taipuvaisia ​​kohti matematiikan kehitystä pitkään. Hahmot, kuten Pythagoras ja Platon, liittyvät numeroihin kaikkeen, mitä maailmassa on. Heille matematiikka oli avain maailmankaikkeuden tulkitsemiseen; Tämä ihanteellinen seurasi Pythagoreans -seuraajia useita vuosisatoja.

Miletus -tarinoita

Tales de Mileto oli yksi ensimmäisistä kreikkalaisista, jotka osallistuivat geometrian kehitykseen. Pitkä aika vietetty Egyptissä ja näistä oppimista perustiedoista. Hän perusti ensimmäisenä geometrian mittauskaavat.

Miletus -tarinoita

Hän onnistui mittaamaan Egyptin pyramidien korkeuden mittaamalla sen varjoa juuri sillä hetkellä, jolloin sen korkeus oli yhtä suuri kuin sen varjon mitta.

Pythagoras

Pythagoras

Pythagorasin merkittävimmällä panoksella (569.C. - 475 a.C.) Geometriaan on kuuluisa Pythagoras -lause, joka osoittaa, että suorakulmiokolmiossa hypotenuusin neliö (oikeaa kulmaa vastustava sivu) on yhtä suuri kuin jäljellä olevien sivujen neliöiden summa.

Euclid -elementit

Muinaisista ajoista lähtien pelastettu tunnetuin työ on ollut tutkimus Elementit, Euclid de alejandríasta (325 a.C. - 265 a.C.), tehty 300 -luvulla.C. Se on suuren historiallisen arvon työ, joka on toiminut matematiikan opettamisessa yli 2000 vuotta.

Euklidi

Elementit Se oli yksi ensimmäisistä kirjoista ja kokoelmista tutkimuksista, jotka selittivät matemaattisia periaatteita, joita voitaisiin soveltaa mihin tahansa tilanteeseen. Sisältää postulaatit, jotka ovat heidän työssään geometrian perusperiaatteita. Toisaalta on olemassa kvantitatiiviset periaatteet, joita kutsutaan peruskäsitteiksi.

Euclid -opetus vähensi geometrian rakennusvälineitä vain kahteen: sääntö ilman toimenpiteitä ja kompassi. Tämä aiheutti kolme klassista ongelmaa, jotka löysivät vastauksia vasta 1800 -luvulla: ympyrän kvadratuuri, kuution päällekkäisyys ja kulman trisektio. 

Voi palvella sinua: Millä vuosisadalla espanjalaiset valloittivat Tenochtitlán?

Muinaisten kohdalla kaksi ihanteellista geometristä kokonaisuutta olivat suora ja ympyrä, joten suurin osa ehdotetuista geometrisistä lauseista oli näiden välineiden etsinnän tuote.

Geometria tähtitieteessä

Geometria hyötyi myös kreikkalaisista tähtien tutkimuksen suhteen. He laskivat liikkeet havainnon läpi ja tekivät taivaan geometriset tasot perustamalla maapallon keskipisteeksi, sekä aurinko ja kuu ja muut niiden ympärillä liikkuvat planeetat ja kokonaisuudet pyörien ympyröissä sarjassa. 

Yksi vaikutusvaltaisimmista panoksista oli Alterin, kirjoitettu toisella vuosisadalla d.C kirjoittanut Claudio Ptolemaios (100 d. C.- 170 d.C), tähtitieteellinen sopimusastio Stars -luettelosta. Se oli aikansa täydellisin teksti ja vaikutti tähtitieteellisiin tutkimuksiin transsendenttisella tavalla keskiajalle erittäin edistyneelle. Se oli osa mediaa, joka suosituin geosentrinen järjestelmä, joka väitti, että maa oli maailmankaikkeuden keskus.

Ptolemaios

Islamilainen vaikutus

Kohti IX vuosisatoja, kun arabimaailma oli suuressa laajentumisessa, suuri osa sen kulttuurista läpäisi useita tieteen ja taiteiden alueita. He olivat suuria kreikkalaisten matemaattisten ja filosofisten teosten faneja. 

Yksi heidän tarpeidensa tutkituimmista oksista oli tähtitiede, jotta voidaan löytää tarkka suuntaus, jossa MECA oli tehdä lauseet.

Euclidin ja muiden Ptolemaios -tutkimusten tutkimusten jälkeen muslimit kehittivät stereografisen projektion, toisin sanoen taivaallisen pallon projektiota koneessa käyttämään sitä karttana. Tämä tarkoitti trigonometrian tutkimuksen edistymistä.

Edustavimpien hahmojen joukossa on Thābit Ibn Qurra (826/36-901), joka teki asiaankuuluvia käännöksiä Apolloniuksen muinaisista teksteistä, Archimedesistä, Euclidista ja Ptolemaiosta. Jotkut näistä ovat ainoat eloonjääneet versiot muinaisista kirjoituksista.

Tähtitieteellistä geometriaa koskevat tutkimukset mahdollistivat myös yhden edustavan välineen, Astrolabion, luomisen, joka yksinkertaisti hetken tähtitieteellisiä laskelmia. Lisäksi tämä instrumentti antoi heille mahdollisuuden tietää aikaa ja lopulta saada ohjeet MECA: lle. 

Se voi palvella sinua: 8 mixtecsin tapoja ja perinteitä

Euroopan perintökehitys

1200 -luvulla kreikkalaisten klassisten opetusten lisäämisen jälkeen muslimien laajentumisen ja heidän samojen löytöjen kehityksen ansiosta latinalaisten tekstien käännökset suoraan kreikkalaisesta alkoi tehdä suoraan kreikkalaisesta tai arabian kielestä. 

Tämä tekisi tietä uudelle Euroopan oppimiselle, jota renessanssi edistää. "Todisteiden" kaltaisten käsitteiden uudelleensijoittaminen alkoi, kreikkalaisten keskuudessa kehitetty käsite, joka oli kiinnostunut postulaattien osoittamisesta todellisuudessa.

Geometria taiteessa

Tieto heijastui myös taiteisiin, kuten maalaukseen tai arkkitehtuuriin, koska geometria alkaisi olla olennainen osa taiteen näkökulman kehitystä.

Filippo Brunelleschi (1377-1446) oli se, joka onnistui kehittämään lineaarisen näkökulman matematiikan kautta. Tämän teorian tavoitteena oli edustaa tasossa kolmen dimensionaalista tilaa siitä, kuinka ihmisen silmä havaitsi sen. Siten se osoittaa, että kaikkien kuvan linjojen piti lähentyä tai löytää vuoto syvyyden tunteen luomiseksi. 

Filippo Brunelleschi. Lähde: I, Sailko/CC BY-S (http: // creativecommons.Org/lisenssit/by-SA/3.0/)

Brunelleschi kuvasi ensimmäisenä näkökulmaa tieteellisenä menettelynä ja tämä toimi seuraavien työpaikkojen perustana taiteessa.

Muissa esimerkeissä geometrian soveltamisesta taiteen ja ihmisen tutkimukseen sinänsä on Leonardo da Vinci (1452-1519) työ hänen piirustuksessaan Vitruvio -mies. Se on tutkimus, joka perustuu ihmiskehon täydellisimpiin mittasuhteisiin sen rakenteen geometrisen analyysin avulla.

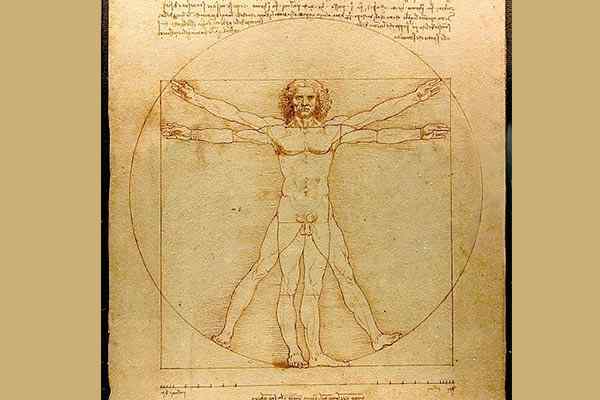Leonardo da Vinci / Public Domain -esittely mies

Myös muun muassa arkkitehtuuri erottuu, missä erilaiset elementit, kuten symmetria ja tasapaino, alkoivat ilmestyä perustavanlaatuisina ominaisuuksina. Neliö, suorakaiteen muotoiset ovet ja ikkunat, sijoitettu tasapainoisella tavalla; Antiikin klassisten elementtien käyttö, kuten sarakkeet, kupolit ja holvat.

Askel nykyaikaisuuteen

Renessanssin aikana näkökulmien ja ennusteiden analyysi oli yksi kannustimista herättää matemaatikkojen kiinnostusta. Tästä hetkestä lähtien geometriassa alkaa perustaa kiinteät ja monimutkaisemmat matemaattiset emäkset.

Yksi nykyaikaisuuden tärkeimmistä teoksista oli arkkitehti Girard Risared (1591-1661), jonka väittivät alun projektille geometrialle. Toisaalta se osoitti, että projisoinnin yhdensuuntaisten linjojen tulisi lähentyä äärettömyyden viivan, ts. Horisontin pisteessä.

Voi palvella sinua: Tuxtepecin kapinan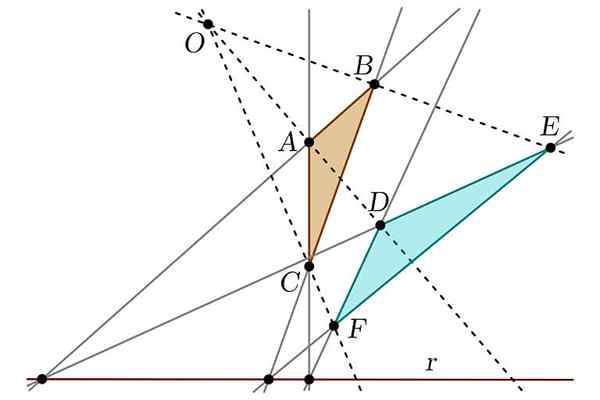Häiriölause

Toisaalta hän löysi myös, mikä tunnustetaan epäjärjestyslauseena, joka luo kahden luvun välisen suhteen, jota voidaan pitää "projektiivisena". Se oli myös vastuussa Apolloniuksen teosten yksinkertaistamisesta kartion osioiden suhteen, mikä tekee analogioita tämän luvun ja sylinterin välillä.

Toinen hieno tapahtuma oli analyyttisen geometrian luominen René Descartesin (1596-1650) ja Pierre de Fermat (1601-1665) tutkimusten avulla itsenäisesti. Tämä on geometrian tutkimus koordinaattijärjestelmän avulla. 

René Descartes työskentelee työpöydälläsi. Wikimedia Commons

Ei -euklidian geometria

Kohti 1800- ja 1800 -luvun tutkimuksia aloitettiin ei -euklidian geometrialla. Erityisesti olivat Gauss, Johann Boleai ja Lobachevsky, jotka havaitsivat, että Euclidin viidennen postulaatin, joka tunnetaan nimellä rinnakkainen postulaatti, ei voitu vahvistaa.

Tällä tavoin he kehittivät eräänlaisen geometrian, jossa tämä postulaatti oli väärin. Tämä uusi muoto onnistui antamalla tyydyttäviä tuloksia geometriatyyleissä, jotka eivät välttämättä täyttäneet kaikkia Euclid -postulaatteja. Siten hyperbolinen geometria ja elliptinen geometria syntyi myöhemmin.

On syytä korostaa Leonhard Eulerin (1707-1783) työtä 1800-luvulla matemaattisen merkinnän kehityksen suhteen. Myöhemmin 2000 -luvulla olisi mukanaan tarkempi geometriakenttien kehittäminen, joiden joukossa on:

-Algebrallinen geometria: Se on matematiikan haara, joka yhdistää abstraktin algebran ja analyyttisen geometrian.

-Rajallinen geometria: Se on geometrinen järjestelmä, joka koostuu rajallisesta määrästä pisteitä, ts. Heillä on loppu tai raja, ja siksi ne voidaan mitata.

-Digitaalinen geometria: Tietotekniikan haara on algoritmien ja tietorakenteiden tutkimus, jota voidaan edustaa geometrisesti. 

Viitteet

1. (2016) mikä teki Euclid -elementeistä ainoan kirjan, joka voi kilpailla Raamatun kanssa. BBC. BBC toipunut.com
2. Kreikan matematiikan kolme klassista ongelmaa. Antioquian yliopisto. Toipunut opetuksesta.sinä.Edu.yhteistyö
3. Heilbron J.L (2020). Geometria. Encyclopædia britannica. Toipunut Britannicasta.com
4. Geometrian historia. Wikipedia, ilmainen tietosanakirja. Haettu jstk.Wikipedia.org
5. Analyyttinen geometria. Wikipedia, ilmainen tietosanakirja. Haettu jstk.Wikipedia.org
6. (2017) Geometria ja matematiikka renessanssissa. Toipunut Ukessaysista.com
7. Sáiz a. Lineaarinen näkökulma Brunelleschissä. Valencian yliopisto. UV toipunut.On
8. Encyclopaedian Britannica (2019) toimittajat (2019). Renessanssiarkkitehtuuri. Encyclopædia britannica. Toipunut Britannicasta.com
9. Andersen K (2020). Girard aseista. Encyclopædia britannica. Toipunut Britannicasta.com
10. (2011) Mielenkiintoinen johdanto laskennalliseen geometriaan. Haettu gaussilaisesta.com