Lagrange -interpolointi

Mikä on Lagrangen interpolointi?

Lagrangen interpolointi on numeerinen menetelmä funktioiden lähentämiselle, mikä käyttää polynomia, joka kulkee tiettyjen funktion tunnettujen pisteiden läpi, jotka on tarkoitettu likimääräiseksi.

Jos likimääräinen funktio on pehmeä, jopa tiedossa olevien tai tunnettujen arvojen ulkopuolella, polynomi ottaa arvot lähelle kiinnostuksen kohteena olevia funktioita, varsinkin jos nämä arvot ovat annettujen pisteiden välillä. Siksi polynomia pidetään hyvänä lähestymistapana toimintoon.

Kuvio 1.- Kaava Lagrange -polynomien rakentamiseksi. Lähde: f. Zapata.

Oletetaan nyt, että haluat arvioida toiminnon f (x) joista vain niiden arvot tunnetaan joissain x-_Yllyttää-, kanssa Yllyttää -sta 0 - siihen asti kun N-1. Eli he tuntevat toisensa n piste (x-_Yllyttää, ja_Yllyttää-A kanssa ja_Yllyttää = f (x_Yllyttää-A, Missä hakemisto Yllyttää Menee 0 - siihen asti kun N-1.

Lagrange -interpolointimenetelmässä funktiota lähestyvä polynomi f (x) Se on polynomi P (x) aste N-1, rakensi lineaarinen yhdistelmä n Polynomit Lens_Yllyttää(x) aste N-1. Nämä ovat Lagrange -polynomit, jotka ilmaistaan ​​seuraavasti:

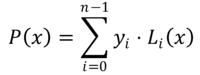
Arvot ja_Yllyttää Ne edustavat abskissaa vastaavia ordinaateja x_Yllyttää Missä funktio f (x) Se on tiedossa, eli: ja_Yllyttää = f (x_Yllyttää-A.

Lagrange -polynomit

Nigrange -polynomit toimivat lineaaristen yhdistelmien kautta perustana rakennusluokan polynomille N -1 joka auttaa interpoloida n tunnettuja pisteitä.

Polynomien merkintä on L_Yllyttää(x), indeksi I: llä välillä 0-N-1. Kaava Lagrange -polynomien perustamiseksi on seuraava:

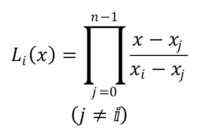
Esitetty symboli osoittaa, että n -1 -monomien tuotekorvaus on suoritettava, alkaen polynomista j = 0.

Lagrange -polynomien ominaisuudet

1.- Lagrange -polynomit ovat täsmälleen samat kuin yksikkö, kun ne arvioidaan niiden hakemistoa vastaavassa absissassa, toisin sanoen:

Lens_Yllyttää(x_Yllyttää) = 1

2.- Ne peruutetaan interpolointipisteiden abskissa -indeksin kanssa, joka on erilainen kuin saman polynomin:

Voi palvella sinua: Kuvailevat tilastot: historia, ominaisuudet, esimerkit, käsitteet

Lens_Yllyttää(x_{J -}) = 0, I ≠ J: n kanssa.

3.- Ottaen muut abskissa -arvot, jotka eroavat interpolointipisteistä, LaGrange -polynomit hankkivat arvot välillä -1 ja +1.

4.- Lagrange -polynomien saamiseksi on tarpeen tietää vain interpoch -pisteiden abskissa.

Toinen -asento lagrange -polynomit

Toinen -asento Lagrange -polynomit ovat niitä, joita käytetään yleisimmin, kun haluat tehdä kolmen pisteen interpoloinnin.

Oletetaan, että interpolaarinen funktio tunnetaan kolmessa pisteessä, jotka ovat:

(x_{0 -},ja_{0 -}-A; (x₁, ja₁-A; (x₂, ja₂-A

Sitten vastaavat Lagrange -polynomit Lens_{0 -}, Lens₁ ja Lens₂ He saavat näin:

Lens_{0 -}(x) = [(x - x₁) / (X_{0 -} - x₁)] [(x - x₂) / (X_{0 -} - x₂)

Lens₁(x) = [(x - x_{0 -}) / (X₁ - x_{0 -})] [(x - x₂) / (X₁ - x₂)

Lens₂(x) = [(x - x_{0 -}) / (X₂ - x_{0 -})] [(x - x₁) / (X₂ - x₁)

On huomattava, että Lens_{0 -}(x_{0 -}) = L₁(x₁) = L₂(x₂) = 1, sillä aikaa Lens_Yllyttää(x_{J -}) = 0 niin kauan kuin Yllyttää≠ J.

Toisen asteen interpolointipolynomi

On tärkeää huomata, että Lagrangen interpoloinnin polynomissa interpolointipisteiden ordinaatit ovat LaGrange -polynomitekijöitä.

Tällä tavoin, kun polynomit on saatu tietyille abskissan arvoille, ne aikovat laskea eri toimintojen interpolointipolynomin, edellyttäen, että aiemmin kiinteässä abskissa on tiedossa.

Toisen luokan interpoloinnin tapauksessa:

P (x) = f (x_{0 -}) L_{0 -}(x) + f (x₁) L₁(x) + f (x₂) L₂(x)

Ja p (x) lähestyy funktiota f (x) aikavälillä (x_{0 -}, x₂-A.

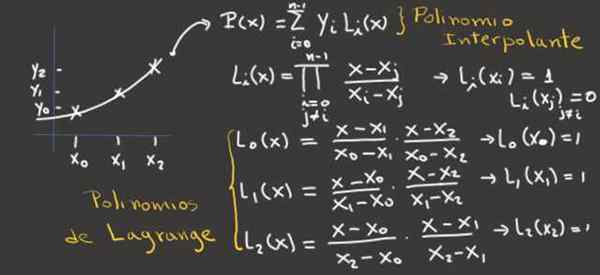Kuva 2.- Tämä kuva näyttää kuinka saada Lagrange -polynomit kolmelle interpolointipisteelle ja niistä, interpoloiva polynomi. Lähde: f. Zapata.

Esimerkit

Esimerkki 1

Etsi Lagrange -polynomit, jotka vastaavat kolmea abskissapistettä x_{0 -}= 0, x₁= 1 ja x₂= 2.

Kuten edellisestä osasta nähdään, nämä polynomit ovat:

Voi palvella sinua: Overjektiivitoiminto: Määritelmä, ominaisuudet, esimerkit

Lens_{0 -}(x) = [(x - 1) / (0 - 1)] [(x - 2) / (0 - 2)] = - (x -1) ⋅ (-½) (x - 2) = ½ ( x² - 3x + 2)

Lens₁(x) = [(x - 0) / (1 - 0)] [(x - 2) / (1 - 2)] = x ⋅ (-1) (x - 2) = - x² + 2x

Lens₂(x) = [(x - 0) / (2 - 0)] [(x - 1) / (2 - 1)] = (½) x ⋅ (x - 1) = (½) (x² - x)

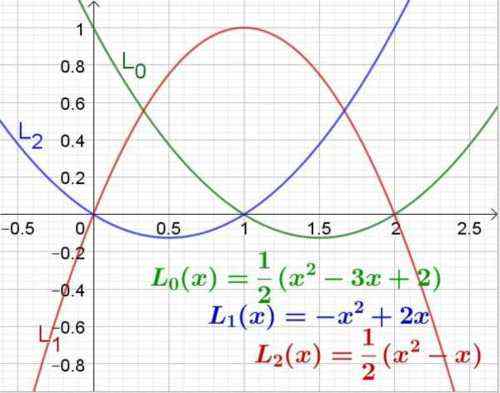Kuva 3. Lagrange -polynomit abscissa -arvoille 0, 1 ja 2. Lähde: f. Zapata.

Esimerkki 2

Haluat arvioida toiminnon f (x) = Arcan (x) Välein [0, 2]. Tästä funktiosta vain niiden arvojen tiedetään x_{0 -}= 0, x₁= 1 ja x₂= 2, jotka ovat vastaavasti ja_{0 -}= 0, ja₁= π/4 = 0,785 ja ja₂= 1 107.

Siksi sinun on löydettävä interpoloiva polynomi P (x) lähestyvä f (x) Ilmoitetulla aikavälillä.

Esimerkissä 1 Lagrange -polynomit on jo määritetty tässä lauseessa ilmoitetuille abskissa -arvoille, joten laskelmaa ei tarvitse toistaa. Polynomin interpolointi on nyt:

P (x) = f (x_{0 -}) L_{0 -}(x) + f (x₁) L₁(x) + f (x₂) L₂(x)

Mikä vastaa:

P (x) = y_{0 -} Lens_{0 -}(x) + ja₁ Lens₁(x) + ja₂ Lens₂(x)

Tässä erityistapauksessa se on:

P (x) = 0 ∙ (½) (x² - 3x + 2) + 0,785 ∙ (- x² + 2x) + 1 107 ∙ (½) (x² - x)

Yllä olevaa on yksinkertaistettu:

P (x) = 0,785 ∙ (- x² + 2x) + 1 107 ∙ (½) (x² - x)

Ja lopuksi pysyy:

P (x) = -0,2315 ∙ x² + 1 0165 ∙ x

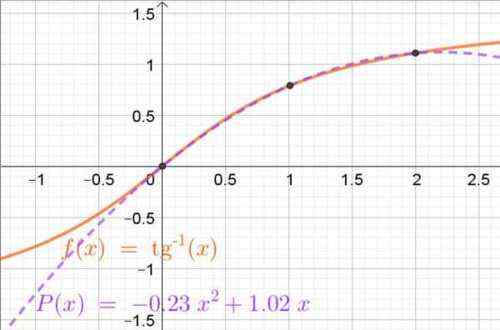Kuva 4. Interpolointi polynomi, joka saadaan Lagrange-polynomien kautta, jotka lähestyvät kaari-todenttista funktiota aikavälillä (0, 2). Interpolointipisteet esitetään myös. Lähde: f. Zapata.

Harjoitukset

Harjoitus 1

Hanki riittävät Lagrange -polynomit lähestymistavan funktioon:

f (x) = sin (x)

Välin [0, π] ja viidellä interpolointipisteellä.

Ratkaisu

Ensinnäkin määritetään interpolointipisteiden abskissa. Tämän kanssa sinulla on:

x_{0 -}= 0; x₁= π/4; x₂= π/2; x₃= 3 π/4; x₄= π.

Voi palvella sinua: kolmion eriarvoisuus: esittely, esimerkit, ratkaisut harjoitukset

Koska f (x) peruutetaan äärimmäisissä kohdissa, lagrange l polynomit L ei ole tarpeen_{0 -} ja minä₄.

Polynomit l₁, Lens₂ ja minä₃ ovat:

Lens₁ = [(x - x_{0 -}) / (X₁ - x_{0 -})] [(x - x₂) / (X₁ - x₂)] [(x - x₃) / (X₁ - x₃)] [(x - x₄) / (X₁ - x₄)

Lens₂ = [(x - x_{0 -}) / (X₂ - x_{0 -})] [(x - x₁) / (X₂ - x₁)] [(x - x₃) / (X₂ - x₃)] [(x - x₄) / (X₂ - x₄)

Lens₃ = [(x - x_{0 -}) / (X₃ - x_{0 -})] [(x - x₁) / (X₃ - x₁)] [(x - x₂) / (X₃ - x₂)] [(x - x₄) / (X₃ - x₄)

Nyt korvaamme abskissan arvo:

Lens₁ = [(x - 0)/(π/4 - 0)] [(x - π/2)/(π/4 - π/2)] [(x - 3 π/4)/(π/4 - 3 π/4)] [(x - π)/(π/4 - π)]

Lens₂ = [(x - 0)/(π/2 - 0)] [(x - π/4)/(π/2 - π/4)] [(x - 3 π/4)/(π/2 - 3 π/4)] [(x - π)/(π/2 - π)]

Lens₃ = [(x - 0)/(3 π/4 - 0)] [(x - π/4)/(3 π/4 - π/4)] [(x - π/2)/(3 π/ 4 - π/2)] [(x - π)/(3 π/4 - π)]

Nimittäjät on ratkaistu:

Lens₁ = [x/π/4] [(x - π/2)/( - π/4)] [(x - 3 π/4)/( - π/2)] [(x - π)/( - 3π/4)]

Lens₂ = [x/π/2] [(x - π/4)/(π/4)] [(x - 3 π/4)/( - π/4)] [(x - π)/( - π /2)]

Lens₃ = [x/(3 π/4)] [(x - π/4)/(π/2)] [(x - π/2)/(π/4)] [(x - π)/( - π/4)]

Sitä yksinkertaistetaan ja ryhmittyvät uudelleen saatuaan:

Lens₁ = x (x - π/2) (x - 3 π/4) (x - π)/( - 3 π ⁴/128)

Lens₂ = x (x - π/4) (x - 3 π/4) (x - π)/(π ⁴/64)

Lens₃ = x (x - π/4) (x - π/2) (x - π)/( - 3 π ⁴/128)

Harjoitus 2

Hanki interpolointipolynomi, joka lähestyy SEN (X) -funktiota aikavälillä [0, π] viidellä harjoituksessa 1 valitulla interpolointipisteellä ja niiden vastaavilla lagrange -polynomeilla.

Ratkaisu

Interpolointipolynomi on:

P (x) = sin (0) * l_{0 -} + Sen (π/4) * l₁ + Sen (π/2) * l₂ + Sen (3π/4) * l₃ + Sen (π) * l4

Sinuksen ja moninkertaistuvan funktion arviointi on:

P (x) = (√2/2) l₁ + 1 * l₂ + (-√2/2) l₃

Vaarallisen algebrallisen työn jälkeen interpolointi polynomi on:

P (x) = 2. 7481 x⁴ -viisitoista. 138 x³ +23. 467 x² - 9. 5236 x

Viitteet

1. Goodman, a. Lens. H. 1996. Algebra ja trigonometria analyyttisellä geometrialla. Pearson -koulutus.
2. Harpe, P. d -d. (2000). Geometrisen ryhmäteorian aiheet. University of Chicago Press.
3. Hazewinkel, M. (2001). Lineaarinen interpolointi ", matematiikan tietosanakirja.
4. Hoffmann, E. (2002). Interpoloinnin kronologiaan: muinaisesta tähtitiedestä nykyaikaiseen signaalin ja kuvankäsittelyyn. IEEE: n julkaisut.
5. Wikipedia. Lagrange -polynomi -interpolointi. Toipunut: Wikipedia.com