Matematiikka

Lineaarinen interpolaatio

Selitämme, mikä on lineaarinen interpoatio, sen kaavat, kuinka tehdä yksi, esimerkit ja harjoitukset ratkaistu

Mikä on lineaarinen interpolointi?

Se Lineaarinen interpolaatio Se koostuu pisteen sijainnin arvioinnista numeerisen välein olettaen, että mainitun aikavälin äärimmäiset arvot yhdistyvät linjalla. Tämän viivan yhtälön tunnetaan, on mahdollista löytää tuntematon kohta.

Idea on suunniteltu seuraavaan kuvaan, joka näyttää lähestymistavan funktion kuvaajaan pisteiden A ja B välillä. Olettaen, että nämä kohdat ovat lähellä, on mahdollista likimääräistä käyrä, joka yhdistää ne linjan läpi ja siten löytää välipisteet.

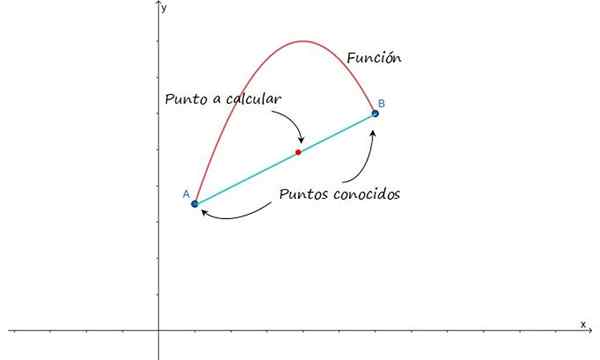Kuvio 1.- Pisteiden A ja B välisen lineaarisen interpoloinnin tekemiseksi on oletettava, että ne yhdistyvät linjalla . Lähde: f. Zapata.

Voit myös lähentää käyrää, joka liittyy pisteisiin, jotka on annettu neliömäisen funktion tai muun polynomin avulla. Linjalla on kuitenkin etuna matemaattisesta yksinkertaisuudestaan, joten se on helppo käsitellä, vaikka se on kaikkien yksinkertaisin interpolointi, on mahdollista, että tulos ei ole niin tarkka kuin käyttämällä muita toimintoja käyttämällä.

Kaavat

Koordinaattia on kaksi [x_jompikumpi, f (x_jompikumpi)] ja [x₁, f (x₁)], joista on kohta [x, g (x)], joiden koordinaatit halutaan tietää.

Ensimmäinen askel koostuu tunnettujen pisteiden yhdistämisestä linjasegmentin kautta, jolle laskennan koordinaatit löytyvät.

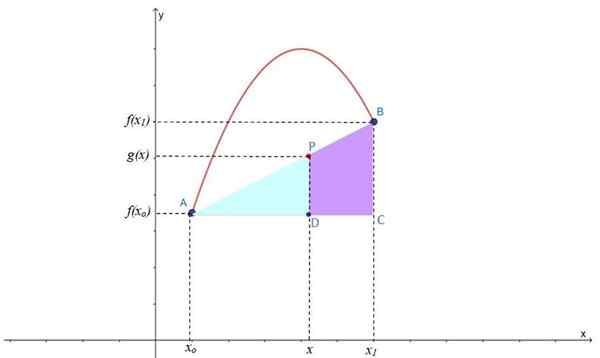Kuva 2.- Lineaarinen interpolointi pisteen P löytämiseksi interpoling -viivalla G (x), joka sijaitsee pisteiden A ja B välillä F (x) välillä. Lähde: f. Zapata.

Kuten näette, muodostuu kaksi suorakulmiota: ABC ja APD, joilla on myös akuutti kulma yhteinen, joten ne ovat samanlaisia kolmioita, joihin Thales -lause voidaan käyttää:

Se voi palvella sinua: analyyttinen geometria

$\fracADAC=\fracAPAB=\fracPDBC$ Segmenttien mittauksen korvaaminen kuvaajan mukaan saadaan seuraava suhde:

$\fracx-x_ox_1-x_o=\fracg(x)-f(x_o)f(x_1)-f(x_o)$ Sieltä jatkamme G (x): n puhdistamista:

$g(x)=f(x_o)+\left [\fracf(x_1)-f(x_o)x_1-x_o \right ]\left ( x-x_o \right )$ Kutsumus:

F₁(x₁) = y₁ ; F_jompikumpi(x_jompikumpi) = y_jompikumpi; g (x) = y

Yläyhtälö muutetaan:

$y=y_o+\left [\fracy_1-y_ox_1-x_o \right ]\left (x-x_o \right )$

Virhealue

Kun funktio lähestyy tällä menetelmällä, virhetaso annetaan funktion f (x) ja interpolointiviivan g (x) välisen eron absoluuttisen arvon perusteella:

Virhe = │f (x) - g (x) │

Kuinka tehdä lineaarinen interpolointi?

Lineaarisen interpoloinnin suorittaminen on hyvin yksinkertaista, sinun on vain noudatettava näitä vaiheita:

Vaihe 1

Määritä tuntematon piste P (x, y).

Vaihe 2

Määritä kaksi pistettä, jotka rajoittavat laskettavan arvon, eli pisteet (x x x x x x x x x x x x x x x_jompikumpi,ja_jompikumpi) ja (x₁, ja₁-A.

Vaihe 3

Korvaa kaikki yhtälön arvot:

$y=y_o+\left [\fracy_1-y_ox_1-x_o \right ]\left (x-x_o \right )$

Ja laske tulos.

Esimerkkejä lineaarisesta interpoloinnista

Esimerkki 1

Haluat löytää ln 3: n likimääräisen arvon lineaarisen interpoloinnin kautta, kun otetaan huomioon seuraavat arvot:

ln 2 = 0.693147 ja ln 4 = 1.386294

Vertaa tulosta laskimen kautta saadun LN 3: n arvoon ja määritetään sitoutunut marginaali.

Vaihe 1

LN 3: n likimääräisen arvon löytämiseksi sinun on jatkettava seuraavalla tavalla: Ensinnäkin tuntematon on määritetty, mikä on y = ln 3, sen vastaavan arvon vieressä “x”: x = 3. Tämä on kohta, jonka haluat laskea: (3, Ln 3).

Vaihe 2

Sitten sinun on määritettävä aikavälin rajapisteet tunnetuilla arvoilla. Sitä pyydetään tekemään niin seuraavilla parilla pisteellä:

Alaraja: [x_jompikumpi = 2; ja_jompikumpi = ln 2 = 0.693147]
Yläraja: [x₁ = 4; ja₁ = ln 4 = 1.386294]
Vaihe 3

Vaiheissa 1 ja 2 määritetyt arvot korvataan yhtälössä huolellisesti LN 3: n lähestymistavan tuloksen tuottamiseksi:

Voi palvella sinua: kuinka monta ratkaisua neliömäisellä yhtälöllä on?

$y=y_o+\left [\fracy_1-y_ox_1-x_o \right ]\left (x-x_o \right )$

$ln\: 3= ln\: 2+\left [\fracln4-ln24-2 \right ]\left (3-2 \right )$
$ln\: 3= 0.693147+\left [\frac1.386294-0.6931474-2 \right ]\left (3-2 \right )=1.039721$ Laskurin saatu LN 3: n todellinen arvo on:

ln 3 = 1.098612

Ja virhemarginaali on:

Virhe = │1.098612 - 1.03971 │ = 0.059

Interpoloinnin prosentuaalinen virhe lasketaan jakamalla virhe LN3: n todellisen arvon välillä ja kertomalla 100 %:

Prosenttivirhe = (todellinen virhe/arvo) × 100 = (0.059/1.098612) × 100% = 5.4%

Esimerkki 2

Nyt haluat löytää LN 3: n likimääräisen arvon lineaarisella interpoloinnilla, tunnet nämä kaksi arvoa:

2.5 = 0.916291 ja LN 3.5 = 1.252763

Määritä myös vastaava virhe ja vertaa edellisen esimerkin tuloksiin.

Vaihe 1

Jälleen tuntematon kohta on:

y = ln 3, x = 3

Vaihe 2
Alaraja: [x_jompikumpi = 2.5; ja_jompikumpi = y_jompikumpi = Ln 2.5 = 0.916291]
Yläraja: [x₁ = 3.5; ja₁ = Ln 3.5 = 1.252763]
Vaihe 3

$y=y_o+\left [\fracy_1-y_ox_1-x_o \right ]\left (x-x_o \right )$

$ln\: 3= ln \: 2.5+\left [\fracln\: 3.5-ln \: 2.53.5-2.5 \right ]\left (3-2.5 \right )=1.084527$ Laskimen tarjoaman arvon tutkiminen:

ln 3 = 1.098612

Virhetaso määritetään tässä tapauksessa, mikä tulokset:

Virhe = │1.098612 - 1.084527 │ = 0.014

Prosenttivirhe tässä tapauksessa on ≈ 1.3 %. Verrattuna esimerkin 1 virhetasoon, uusi arvo on tarkempi, koska interpolariin valittu aika on alhaisempi.

Ratkaisut

Harjoitus 1

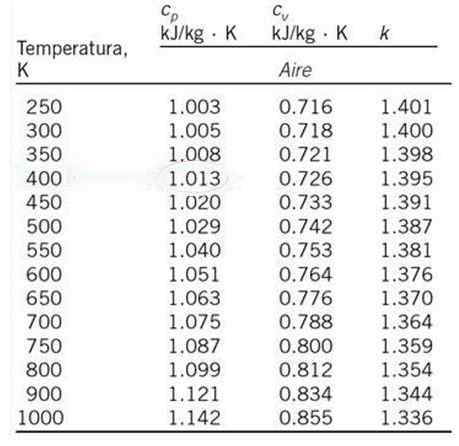
Laske lineaarisella interpoloimalla ilman ominaislämpö vakiopaineessa c_p ja lämpötila 530 K, alkaen alla esitetystä arvotaulusta.

Ratkaisu

Monien ongelmien ratkaisemisessa on yleistä, että haettava arvo ei näytä tarkalleen halutun arvotaulukossa. Vaihtoehto on valita haluttu.

Voi palvella sinua: ryhmittelyn merkkejä

C: n arvo_p 530 K: tä ei näy kiinnittyneessä taulukossa, mutta lineaarinen interpolointi voidaan tehdä vastaavilla erityisillä lämmityksillä 500 K: n ja 550 K: n lämpötilassa, jotka ovat lämpötiloja, jotka ovat lähinnä 530 K: ta ja joiden erityisiä lämmittelyjä esiintyy esitetyssä taulukossa.

Näiden lämpötilojen vastaavat erityiset lämpölämpöt ovat:

T_jompikumpi = 500 K; c_poikki = 1.029 kJ /kg ∙ k

T₁ = 550 K; c_P1 = 1.040 kJ /kg ∙ k

Ja tuntematon on kohta (500k, c_p-A

Korvataan yllä annetun lineaarisen interpoloinnin kaavassa t muuttujan "x" ja c tapahtumapaikalla_p "Y": n sijasta sinulla on:

$y=y_o+\left [\fracy_1-y_ox_1-x_o \right ]\left (x-x_o \right )$

$c_p= c_po+\left [\fracc_p1-c_poT_1-T_o \right ]\left (T-T_o \right )$

$c_p= 1.029+\left [\frac1.040-1.029550-500 \right ]\left (530-500 \right )\frackJkg\cdot K=1.03536\frackJkg\cdot K$

Harjoitus 2

Jousiin kohdistettu kuorma (kilopondioissa) tuottaa seuraavat pidentymiset (millimetreinä) esitetyn taulukon mukaisesti:

Laske pidennys, kun kuorma on 12.6 kp.

Ratkaisu

Let ja pidentymisen arvo, kun kuorma on c = 12.6 kp. Tuntematon kohta on (12.6, y), joka on pisteitä:

C_jompikumpi = 10 kp; ja_jompikumpi = 105 mm

C₁ = 15 kp; ja₁ = 172 mm

Se on jäljellä vain yhtälön arvojen korvaamiseksi:

$C= 105+\left [\frac172-10515-10 \right ]\left (12.6-10 \right )\: mm=139.84\: mm$ Ehdotettu harjoitus

Laske spesifinen lämpölämpö vakiotilavuuteen 727 K: n lämpötilassa käyttämällä lineaarista interpolointia ja harjoituksen arvopaperitaulua ratkaistu 1.

Viitteet

Rafa Vilchez Academy. Kuinka suorittaa lineaarinen interpolointi. Toipunut: AcademiraafaVilchez.com
Chapra, s. 2007. Numeeriset menetelmät insinööreille. Viides. Painos. McGraw Hill.
Khan -akatemia. Lineaarisen interpoloinnin matematiikka. Toipunut: khanacademy.org.
Koulutuselämä. Lineaarinen interpolointikaava. Palautettu: TheDucationLife.com
X-internoi. Lineaarinen interpolointi ja ekstrapolointi laskimen kanssa. Toipunut: x-insinööri.org.

Lineaarinen interpolaatio

Mikä on lineaarinen interpolointi?

Kaavat

Virhealue