Moninkertainen käänteinen selitys, esimerkit, harjoitukset ratkaistu
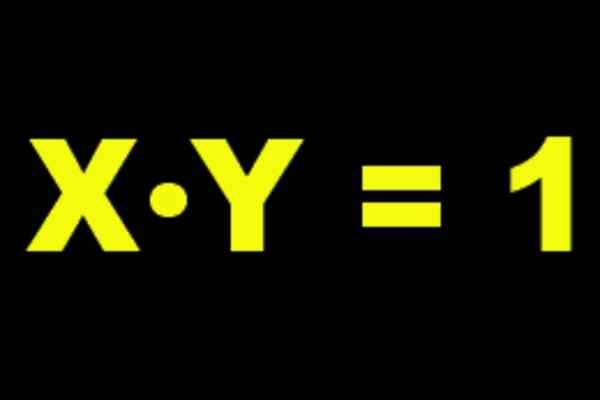
- 1502
- 195
- Juan Breitenberg V
Se ymmärretään Käänteinen moninkertainen yhdestä numerosta toinen numero, joka kerrottuna ensimmäisellä tuloksella tuotteen neutraaliin elementtiin, toisin sanoen yksikkö. Jos sinulla on todellinen numero -lla Sitten hänen moninkertainen käännös on merkitty -lla-1, Ja se on täytetty, että:
a-1 = a-1 A = 1
Yleensä numero -lla Se kuuluu todellisten lukujen joukkoon.
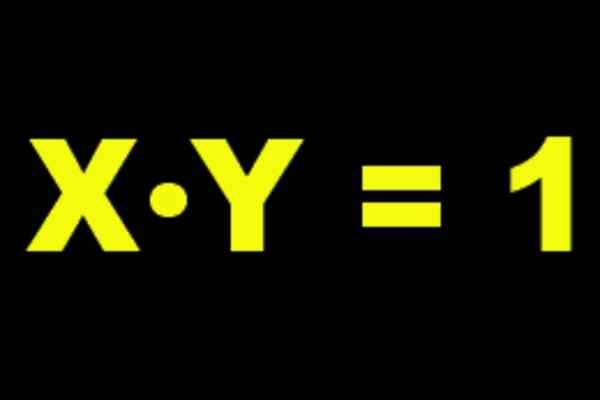 Kuvio 1. Ja se on käänteinen kertoimen x ja x on moninkertainen käänteinen Y: n.
Kuvio 1. Ja se on käänteinen kertoimen x ja x on moninkertainen käänteinen Y: n. Jos esimerkiksi otamme A = 2, Sitten moninkertainen käänteinen on 2-1 = ½ Koska seuraava on varmennettu:
2 ⋅ 2-1 = 2-1⋅ 2 = 1
2⋅ ½ = ½ ⋅ 2 = 1
Siihen Käänteinen moninkertainen lukumäärästä kutsutaan myös vastavuoroinen, Koska moninkertainen käännös saadaan vaihtamalla numeroija ja nimittäjä, esimerkiksi 3/4: n moninkertainen käännös on 4/3.
Pääsääntöisesti voidaan sanoa, että rationaaliseen lukumäärään (P/q) Kerrottava käänteinen (p/q)-1 Se on vastavuoroinen (Q/p) Kuten alla voidaan vahvistaa:
(p/q) ⋅ (p/q)-1 = (p/q) ⋅ (q/p) = (p⋅ q)/(q⋅ p) = (p⋅ q)/(p⋅ q) = 1
Moninkertaista käänteistä ei ole kokonaislukujen numeerisessa sarjassa, Esimerkiksi, jos koko numero 2 otetaan, sen moninkertainen käänteinen sen mukaan, mitä yllä nähtiin, olisi ½, mutta ½ ei ole kokonaisluku.
On myös kertolaskujen kertoimen käänteinen käännös. Toisin sanoen nolla -numerolla (0), joka on kertolaskuoperaation nollaelementti, ei ole kertolaskuinen käänteinen, koska yksikön nollalla ei ole lukumäärää, joka ei kerrottu nollalla.
Moninkertainen käänteinen on rationaalisesti, reaalilukuina ja kompleksilukuina.
Moninkertaiset käänteiset esimerkit
Esimerkki 1
Löydä 3/2 kerroksen käänteinen ja varmista, että se vastaa moninkertaisten kokonaislukujen ominaisuuksia.
Voi palvella sinua: Coplanares -pisteet: Yhtälö, esimerkki ja ratkaisut harjoituksetEdellä annetun säännön mukaan (3/2): n moninkertainen käänteinen käännös vaihdetaan tällä tavalla. Kahden numeron kertolasku on suoritettu:
(3/2) ⋅ (2/3) = (3 ⋅ 2)/(2 ⋅ 3) = 6/6 = 1.
Kerrota kaksi murto -lukua kerrotaan vain toisen numeroijan ensimmäisen numeroijaksi tulosten numeraattorin saamiseksi.
Jatkoa koskevan tuotteen nimittäjän saamiseksi, etenee samalla tavalla, toisin sanoen nimittäjät kerrotaan keskenään ja tulos on tuotteen nimittäjä. Esimerkissämme on varmennettu, että numeron ja sen vastavuoroisen tuotteen osoitin on 6 ja nimittäjä 6, jättäen murto -osan 6/6, joka on 1.
Esimerkki 2
Kerroava käänteinen -5 ei pidä sekoittaa sen symmetriseen (+5), jota joskus kutsutaan aritmeettiseksi käänteiseksi. Moninkertainen käännös saadaan seuraavasti:
(-5) ⋅ x = 1
Missä x on kertoimen käänteinen hankittava. Mahdollinen menettely koostuu tuntemattoman x: n puhdistamisesta. AS (-5) kertoo tuntemattoman X: n vasemmassa jäsenessä, niin se tapahtuu jakamalla oikea jäsen:
X = 1 / (-5)
Kuten tiedetään + välillä - se on - sitten lopulta x saadaan:
X = - ⅕ .
Yhteenvetona - ⅕ on moninkertainen käänteinen -5.
Esimerkki 3
Hanki moninkertainen käänteinen -√2. Oletetaan
-√2 ⋅ x = 1
Molemmat jäsenet jaetaan - -Häntä saadaan:
(-√2 ⋅ x) / (-√2) = 1 / (-√2)
Ensimmäinen jäsen yksinkertaistetaan -"jäljellä:
Se voi palvella sinua: Vakio arviointivirhe: miten se lasketaan, esimerkkejä, harjoituksiaX = 1 / (-√2)
Tämä lauseke voidaan rationalisoida, toisin sanoen nimittäjän juuren eliminoimiseksi, kertomalla numeroijalla (-√2) ja nimittäjällä saman määrän suhteen, jotta tulosta ei muuteta:
X = (-√2) / [(-√2) (-√2)] =-(√2 / 2)
Yhteenvetona - (√2/2) on moninkertainen käänteinen (-√2).
Esimerkki 4
Oletetaan mikä tahansa numero x, hanki kertolasku käänteinen ja edusta sitä graafisesti.
Tässä tapauksessa se on funktio f (x) = x, moninkertaisen käänteisen hankkiminen on löytää funktio g (x) siten, että kerrotaan yksikön ensimmäisellä yksiköllä. G -funktio on F: n vastavuoroinen funktio, eikä sitä pidä sekoittaa millään tavalla käänteisen toiminnan kanssa.
Toisin sanoen X: n moninkertainen käänteinen käänteinen on a ja siten, että seuraava on toteutettu:
x ⋅ y = 1
Missä puhdistaa ja olla:
y = 1/x.
Edellä oleva tulkitaan siten, että X: n arvo on, edellinen kaava antaa meille sen moninkertaisen käänteisen.
Sen graafinen esitys on mahdollista tehdä seuraavassa kuvassa:
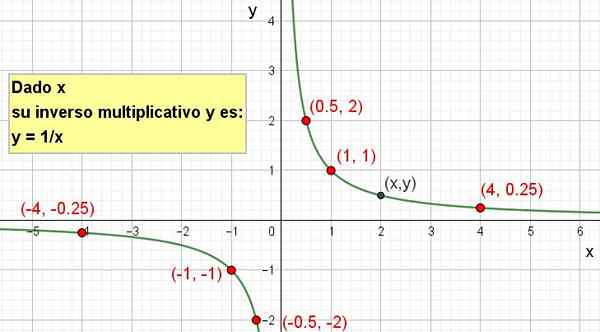 Kuva 2. X: n kerroin käänteinen käänteinen on y = 1/x.
Kuva 2. X: n kerroin käänteinen käänteinen on y = 1/x. Harjoitukset
Harjoitus 1
Annetaan x = 2 - √2, hanki moninkertainen käänteinen ja.
Ratkaisu:
Joten se on moninkertainen x x
x ⋅ y = 1
X korvataan sen arvolla:
(2 - √2) ⋅ y = 1
Sitten se puhdistuu ja:
y = 1 / (2 - √2)
Tuloksen rationalisointi moninkertaistaa numeroijan ja nimittäjän sen konjugoidulla binomilla:
y = (2 + √2) / ((2 + √2) (2 - √2))
Nimittäjässä tunnistetaan huomattava tuote, jota kutsutaan eron summan tuoteeksi, mikä on neliöiden ero. Tällä tavalla juuri katoaa nimittäjästä.
y = (2 + √2) / (2^2 - (√2)^2)
Voi palvella sinua: osuusVoimien ratkaiseminen:
y = (2 + √2) / (4 - 2)
Yksinkertaistaminen:
y = (2 + √2) / 2
Harjoitus 2
Hanki moninkertainen käänteinen (1/a + 1/b), missä a ja b ovat erilaisia reaalilukuja.
Ratkaisu:
Kutsumme (1/a + 1/b) moninkertainen käänteinen, jotta seuraava yhtälö on täytettävä:
Ja ⋅ (1/a + 1/b) = 1
Muuttuja puhdistetaan ja:
Y = 1/(1/a + 1/b)
Nimittäjä on ratkaistu:
Y = 1 / ((b + a) / a b)
Kuten algebran säännöistä tiedetään, nimittäjän nimittäjä siirtyy numeraattoriin:
Y = (a b) / (b + a)
Sitä käsketään lopulta hankkimaan:
(a b)/(a + b), joka on (1/a + 1/b) kerroin käänteinen käänteinen käänteinen.
Harjoitus 3
Hanki moninkertainen käänteinen (a - b) / (a^2 - b^2).
Ratkaisu:
Muista, että moninkertaista käänteistä kutsutaan myös vastavuoroiseksi, koska se saadaan vain vaihtamalla numeroijaa ja nimittäjää.
Sitten moninkertainen käänteinen (a - b) / (a^2 - b^2) on:
(A^2 - B^2) / (A - B)
Mutta tätä ilmaisua voidaan yksinkertaistaa, jos tunnustamme algebran sääntöjen mukaan, että numeraattori on neliöiden ero, joka voi olla ottanut huomioon eron summan tuote:
((A + b) (a - b)) (a - b)
Koska numeraattorissa on yleinen tekijä (a - b) ja jatkamme nimittäjän yksinkertaistamista, lopulta saadaan: lopulta:
(A + B), joka on moninkertainen käänteinen (a - b) / (a^2 - b^2).
Viitteet
- Lähteet, a. (2016). Perusmatiikka. Johdatus laskelmaan. Lulu.com.
- Garo, m. (2014). Matematiikka: neliömäiset yhtälöt: Kuinka ratkaista neliömäinen yhtälö. Marilù garo.
- Haeussler, E. F., & Paul, r. S. (2003). Matematiikka hallinto- ja taloustieteelle. Pearson -koulutus.
- Jiménez, J., Rofríguez, M., & Estrada, r. (2005). Matematiikka 1. syyskuuta. Kynnys.
- Arvokas, c. T. (2005). Matematiikkakurssi 3o. Toimitusohjelma.
- Rock, n. M. (2006). Algebra I on helppo! Niin helppoa. Team Rock Press.
- Sullivan, J. (2006). Algebra ja trigonometria. Pearson -koulutus.

