Fickin laki

Mikä on Fickin laki?

Se Fickin laki Se on matemaattinen yhtälö, joka liittyy väliaineeseen levitetyn massavirtauksen pitoisuuksien tai painegradientin kanssa. Sen muotoili vuonna 1855 saksalainen fysiologi ja tohtori Adolf Fick, jotka inspiroivat Fourierin lakeja (lämmönjohtavuus) ja OHM (sähköinen johtavuus), mallitsi hapen diffuusioprosessin keuhkojen alveoleihin.

Fickin laissa esitetään erityisyys, että sitä ei sovelleta pelkästään kemiallisiin tai biokemiallisiin diffuusioilmiöihin, vaan myös minkäänlaisiin luonteisiin. Siksi sen tarkoituksena on mallintaa atomien leviämistä kiinteiden aineiden välillä, mikä on erittäin hyödyllinen materiaalien ja tekniikan fysiikassa.

Diffuusioprosessin esitys puolijalkavertaisen kalvon kautta. Lähde: Gabriel Bolívar.

Keskuspohja on kuitenkin sama melkein kaikissa diffuusioilmiöissä, jotka on esitetty yllä. Violetti hiukkaset, atomit tai molekyylit, levitetään puolipesäkevään paksun kalvon L ja poikittaisalueen läpi. Vasemmalla on suurempi pitoisuus C₁ hiukkasia, jotka oikealla, c₂.

Fickin laki vahvistaa seuraavan: pinnan läpi levitetty massavirta on verrannollinen pitoisuusgradienttiin (C₂-C₁/L) ja vakio d, jota kutsutaan diffuusio- tai diffuusiokerroin.

Tällä lailla on kaksi muotoa: yksi avaruuteen (x) perustuva ja toinen tilasta ja ajasta riippuen (x, t). Ensimmäinen sovelletaan järjestelmiin paikallaan olevissa olosuhteissa, kun taas toinen todellisille, ei -osa -alueille.

Fickin ensimmäinen laki

Komponentit ja yhtälö

Puoliläpäisevän kalvon paksu l edustaa etäisyyttä (x), että hiukkasten on kuljettava pääsemään toiselle puolelle. Kuten kuvassa voidaan nähdä, purppurahiukkaset, sitä enemmän ne siirtyvät vasemmalta osastolta, missä C₁ Se on suuri, sen pitoisuus laskee C: n arvoon₂. Toisin sanoen pitoisuus muuttuu kalvon paksuuteen, riippuen x: stä.

Tämä pitoisuuden vaihtelu etäisyydestä riippuen tunnetaan pitoisuusgradientina: (C₂-C₁)/L o (c₂-C₁)/x. Huomaa, että sen arvo on negatiivinen (-1), koska c₂ > C₁.

Toisaalta meillä on myös nopeus, jolla hiukkaset leviävät kalvon tai kyseisen tilan läpi. Tämä nopeus riippuu hiukkasten koosta ja massasta, samoin kuin ympäristön ja lämpötilan luonteesta. Diffuusiokerroin D edustaa tätä nopeutta ja voi olla vakio tai ei diffuusion aikana.

Voi palvella sinua: laboratoriosuodatin): Ominaisuudet, toiminnot, tyypit

Ja lopuksi, meillä on massavirta 'J', joka ylittää kalvon poikittaisen alueen tai kanavan, jossa hiukkaset leviävät. Näiden termien ryhmittely, Fickin ensimmäisen lain yhtälö syntyy:

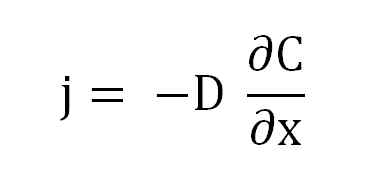Yhtälö Fickin ensimmäisestä laista. Lähde: Gabriel Bolívar.

Missä J on verrannollinen D ja A (∂c/∂x), pitoisuusgradientti.

Tulkinta ja yksiköt

Yhtälön negatiivinen symboli auttaa negatiivisten pitoisuuksien gradientin negatiivisen merkin. Muutoin j: llä olisi negatiivinen arvo, joka on kiinnittynyt. Samoin D: n arvo on positiivinen, joten kertomalla sitä edeltäneellä negatiivisella merkkillä, se antaa negatiivisen arvon.

Fickin ensimmäinen laki osoittaa seuraavan: Mitä suurempi pitoisuusgradientti (∂c/∂x), sitä suurempi massavirta j. Eli ero c: n välillä₂ ja c₁ Se tulee suuremmaksi ja siksi enemmän hiukkasia leviää kalvon läpi.

Toisaalta J riippuu myös D: stä, joka puolestaan ​​riippuu parametreista, kuten lämpötilasta, viskositeetista, molekyylipainosta ja poikittaisesta alueesta:

D ∝ (a/l) (s/√M_{W -}-A

Missä S on ympäristön kanssa leviävän hiukkasen liukoisuus ja m_{W -} Sen molekyylipaino.

Suhteessa yhtälön komponenttien tai ehtojen yksiköihin:

-C (kg · m^-3 tai mol · m^-3-A

-D (m^-2·^-1-A

-J (kg · m^-2·^-1 tai mol · m^-2·^-1-A

Nettoväliaineen neliömäinen siirtymä

Leviämisen aikana hiukkaset törmäävät toisiinsa, ja lyhyen ajanjakson jälkeen lopulta kulkevat valtavia etäisyyksiä ΔX. Näiden siirtymien merkityksestä riippuen AX: llä voi kuitenkin olla negatiivisia tai positiivisia arvoja (lähtökohdan mukaan). Siksi kaikkien molekyylien AX -arvojen keskiarvo on 0.

Toisaalta, AX -arvot ovat hyvin pienet verrattuna hiukkasia ajaviin etäisyyksiin. Kun he törmäävät, he menettävät liikkuvuuden suuntaan, joten nettosiirto on rajoitettu; Esimerkiksi 2 cm etenee yhteen suuntaan matkustaakseen satoja metrejä törmäyksissä ja palautumisissa.

Einstein vuonna 1905 löysi matemaattisen lausekkeen siirtymän keskimääräiselle vieritykselle (siksi erilainen kuin 0):

<(Δx)²> = 2dt

Määrittelevä

(Δx)_Rms ≡ <(Δx)²-^1/2 = (2dt)^1/2

(Δx)_Rms Se on kyseisten hiukkasten keskimääräinen netto neliöllinen siirtymä. (Δx)_Rms Se kertoo meille, kuinka paljon hiukkasia liikkuu keskimäärin (positiiviseen tai negatiiviseen suuntaan) ajan mukaan. Jotkut hiukkaset liikkuvat pidemmälle tai lähinnä etäisyydet kuin (Δx)_Rms, aiheuttaen Gaussin jakauman.

Voi palvella sinua: kalsiumoksidi (CAO)

Fick toinen laki

Yhtälö

Fickin ensimmäinen laki kuvaa diffuusiota paikallaan olevissa olosuhteissa, ts. Massavirta j ei vaihtele ajan myötä. Oikeissa järjestelmissä meillä on kuitenkin ei -asunto -olosuhteita, joissa massavirta ei vain vaihtele avaruudessa, vaan myös ajan myötä. Siksi se on kiinnostunut määrittämään (∂c/∂t).

Alla on kaksi yhtälöä, jotka edustavat Fickin toista lakia:

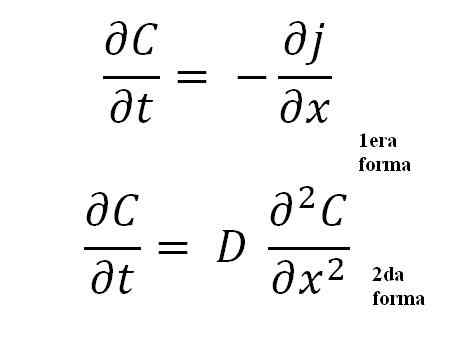Fickin toisen lain yhtälöt. Lähde: Gabriel Bolívar.

Toinen muoto on tärkein kaikista, koska se edustaa yleistä matemaattista yhtälöä mille tahansa levitysprosessille; joko lämpö-, sähkö-, atomi- jne.

Vähennys

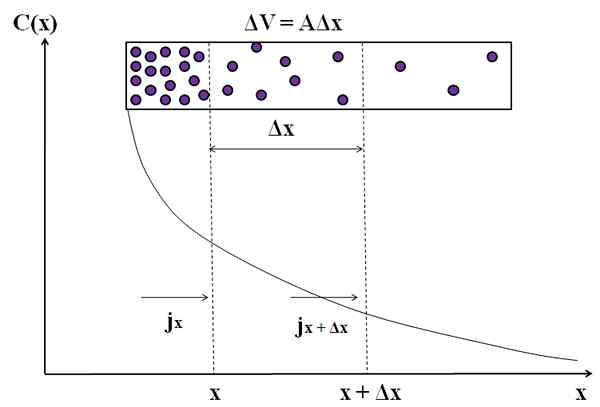Graafinen esitys siitä, kuinka massavirta ei ole vakio näiden molekyylien leviämisessä. Lähde: Gabriel Bolívar.

Harkitse jälleen purppurahiukkasia suorakaiteen muotoisessa kammiossa. Etäisyyksistä x ja x+Δx meillä on virtaus j_x (saapuva) ja J_x+Δx (lähtevä). Kameran äänenvoimakkuus näiden etäisyyksien välillä on määritelty:

ΔV = AAX

Huomaa, että kaavio C (x) vs x ei ole suoraa, joten meillä on erilaiset arvot J (J_x ≠ J_x+Δx-A. Meidän on määritettävä Δc/Δt.

Massa m_x Se on yhtä suuri kuin:

m_x = J_x At

Mittaanalyysi auttaa ymmärtämään miksi:

kg = (kg · m^-2·^-1) (m²) (S)

Samoin kuin laskemme m_x+Δx-

m_{x+ Δx} = J_x+Δx At

On massa, joka kertyy kyseiseen alueelle, joka on yhtä suuri kuin ΔM:

Δm = m_x - m_{x+ Δx}

= (J_x - J -_{x+ Δx}) Aδt

= -(J_{x+ Δx} - J -_x) Aδt

= -AJAt

Ja tietäen, että Δc = ΔM/ΔV

Δc = -Ajaδt/ ΔV

= -AJAAT /AAX

= -AJδT/AX

Puhdistamme Δc/ΔT

Δc/ΔT = -AJ/Δx

Tämä ekspressio osoittaa, että pitoisuuden vaihtelu ajan myötä on yhtä suuri kuin J -virtauksen vaihtelu sen siirtymisen suhteen. AT: n ja Δx: n rajojen soveltaminen 0: een saamme saman ekspression kuin osittainen johdannainen:

∂c/∂t = -(∂j/∂x) (1. muoto)

Lopuksi toinen muoto saadaan korvaamalla J Fickin ensimmäisellä lailla:

∂c/∂t = -∂/∂x (-d∂c/∂x)

= D (∂²C/∂x²) (2. muoto)

Ratkaisut

Seuraavissa harjoituksissa harkitaan hyvin yksinkertaisia ​​järjestelmiä, joiden tuntemattomat voidaan ratkaista Fickin ensimmäisellä lailla.

Harjoitus 1

Lausunto

Putkessa 15 metriä pitkä ja 21 senttimetriä leveä ja joka on myös kyllästetty typellä, happivirta leviää päästä toiseen lämpötilassa 0 ºC. Tietäen, että paine vasemmalla puolella (P₁) on 20 kg/m³, Ja että paine oikealla puolella (P₂) on 10 kg, määritä:

Se voi palvella sinua: Hydronio -ioni

a) leviävä massavirta

b) kuinka monta kiloa tai₂ Ne leviävät putken läpi 17 minuutissa?

c) pitoisuusgradientti tai paineet

d) O: n paine₂ 7 metrin etäisyydellä putkilinjan sisäänkäynnistä

e) kuinka paljon 80 kg O: ta₂ Leviäessä tämän putken läpi?

Mieti sitä d_O2-N2 on yhtä suuri kuin 1.8 · 10^-5 m²·^-1.

Ratkaisu

Fickin ensimmäisestä laista meidän on ratkaistava a alakohta a):

J = -d (P₂-P₁)/L

= -(1.8 · 10^-5 m²·^-1) (10-20) (kg/m³)/(15 m)

= 1.2 · 10^-5 kg · m^-2·^-1

B) tarvitsemme putken alueen:

A = π (0.21 m)²

= 0.14 m²

Ja kerrotaan j a ja aika t määrittääksesi tai₂ Välitön:

m_O2 = (1.2 · 10^-5 kg · m^-2·^-1) (17 s) (0.14 m²-A

= 3.57 · 10^-5 kg

Nyt alajaksoon c) meillä on, että gradientti on yhtä suuri kuin:

Gradientti = (P₂-P₁)/L

= (10-20) (kg/m³)/15 m

= -2/3 (kg/m³) · M^-1

Mutta otamme positiivisen arvon, mikä on fyysistä järkeä:

2/3 (kg/m³) · M^-1

Tämä arvo palvelee meitä sitten ratkaisemaan alajakson d), jos gradientti tulkitaan hyvin: jokainen metri PAINE OR: n tai₂ 2/3 kg/m putoaa³. Levittämällä 7 metriä, meillä on:

2/3 (kg/m³) · M^-1 (7 m) = 14/3 tai 4.7 kg/m³

Eli paine etäisyydellä on:

(20-4.7) (kg/m³) = 15.3 kg/m³

Ja lopuksi, alajakso e) on samanlainen kuin b), vain että nyt puhdistamme aika eikä massa:

m_O2 = Jat

t = m_O2/Ja

= (80 kg)/(1.2 · 10^-5 kg · m^-2·^-1) (0.14 m²-A

= 47619.04 s tai 0.55 päivää

Harjoitus 2

Lausunto

Määritä (Δx)_Rms Sakkaroosille vedessä t = 1 min, 1 h ja 1 päivä. Sakkaroosin levityskerroin vedessä on 0.52 · 10^-5cm²·^-1.

Ratkaisu

Käytämme yhtälöä:

(Δx)_Rms ≡ <(Δx)²-^1/2 = (2dt)^1/2

Arvioimme (Δx)_Rms Ajat ilmaistuna sekunnissa. T = 1 min tai 60 s:

(Δx)_Rms = ((2 (0.52 · 10^-5cm²·^-1) (60s))^1/2

= 0.025 cm

T = 1 h tai 3600 s:

(Δx)_Rms = ((2 (0.52 · 10^-5cm²·^-1) (3600 s))^1/2

= 0.19 cm

Ja lopuksi t = 1 päivä tai 86400 s:

(Δx)_Rms = ((2 (0.52 · 10^-5cm²·^-1) (86400s))^1/2

= 0.95 cm

Huomaa, että sakkaroosimolekyylien ajan kuluessa ei ole edes pystynyt liikkumaan 1 cm mihin tahansa suuntaan.

Viitteet

1. Walter J. Moore. (1963). Fysikaalinen kemia. Kemiallisessa kinetiikassa. Neljäs painos, Longmans.
2. Iranin. Levine. (2009). Fysikaalis -periaatteet. Kuudes painos. MC Graw Hill.
3. Johdanto materiaalitieteeseen ja tekniikkaan. (11. maaliskuuta 2018). Fickin toinen laki. Prof. Rajesh Prasad. [VIDEO]. Palautettu: YouTube.com
4. Wikipedia. (2020). Fickin levityslakeja. Haettu: vuonna.Wikipedia.org
5. Laura Dickson. (10. syyskuuta 2020). Levitys. Kemian librettexts. Palautettu: Chem.Librettexts.org
6. Larissa Zhou et ai. (1. syyskuuta 2015). Diffuusioteorian ja Fickin lain ymmärtäminen ruoan ja ruoanlaiton avulla. Amerikkalainen fysiologinen yhdistys. doi.org/10.1152/Advan.00133.2014