Usean mittasuhteen laki

Mikä on useiden mittasuhteiden laki?

Se Usean mittasuhteen laki Se osoittaa, että jos kaksi elementtiä muodostavat useamman kuin yhden yhdisteen, kun ne reagoivat toisiinsa, niin niiden massojen osuus, joiden kanssa yksi niistä yhdistetään kiinteään massaan, se on yhtä suuri kuin pienten lukujen suhde.

Lain lausunto voi tuntua monimutkaiselta, jos sinulla ei ole esimerkkiä käsillä. Siksi harkitse joitain Oreos -evästeitä, jotka koostuvat kahdesta suklaakannasta ja sokerivoiteen nauhasta: t: t₂C (t = kansi ja c = kerma). Jos halusimme keksiä vankemman Oreo -evästeen, lisäisimme toisen kermanauhan, jotta saamme kaksinkertaisen kerman (t₂C₂ tai tc).

Jälkiruoissa, kuten Oreos -evästeissä. Lähde: Brokensphere, CC BY-SA 3.0 https: // creativecommons.Org/lisenssit/by-SA/3.0 Via Wikimedia Commons

Voisimme myös lisätä toisen, niin että evästeellä on kolme kertaa enemmän kermaa kuin tavanomaisella evästeellä (t₂C₃-A. Entä jos laitamme uuden suklaan kannen valkoisten raitojen keskelle (t₃C₂-A? Vaihtoehdot ovat rajoittamattomia; Mutta lisäämme aina kannen tai kermayksikön. Emme ajattele puolta kannen (1/2 t) tai viidesosaa kermasta (1/5 c), koska se olisi sopimatonta.

Samalla tavalla se tapahtuu kemiallisten elementtien kanssa: niiden atomit eivät jaa yhdisteiden muodostamiseksi. Siksi T- tai C -massat niiden yhdisteiden joukossa "aina" yksinkertainen suhde.

Selitys

Mittasuhteet

Useiden mittasuhteiden laki yhdessä määritettyjen mittasuhteiden lain kanssa edelsi stökiometriaa ja ensimmäisiä kemiallisia kaavoja. Unohdetaan evästeet, mutta pidetään heidän symbolit: t ja c. Kokeiden avulla havaitaan, että elementit T ja C muodostavat useita yhdisteitä: t₂C, TC ja T₂C₃.

Ennen kemiallisia kaavoja oli mahdotonta tietää kerralla, jotka olivat T- ja C -massojen mittasuhteita sellaisissa yhdisteissä. Piti ensin määrittää ne. Yhdisteessä havaittiin, että T: n massa kaksinkertaistui C: n massaan; Sanoa, 2 grammaa T: tä yhdistetään 1 grammaan c.

Voi palvella sinua: kapasitanssi: yksiköt, kaavat, laskelmat, esimerkit

Sitten toisessa yhdisteessä T- ja C -massat oli sovitettava: 2 grammaa T: tä yhdistetään nyt 2 grammaan C: n kanssa. Tässä nousee kysymys: Entä jos T ja C voivat silti muodostaa toisen yhdisteen? Jos näin on, se muodostetaan varmasti 2 grammaa t: lla, mutta tällä kertaa ne yhdistetään 3 grammaan C: n (1 gramma + 1 gramma + 1 gramma).

Yksinkertaiset massasuhteet

Niiden massojen mittasuhteet, joiden kanssa T- ja C React sallivat niiden kemiallisten kaavojen määrittämisen: t₂C (2 grammaa t: 1 gramma c), tc (2 grammaa t: 2 grammaa c) ja t₂C₃ (2 grammaa t: 3 grammaa c). Jos haluamme verrata näiden yhdisteiden T- tai C -massojen suhteita, on välttämätöntä, että yksi sen massoista pysyy vakiona; Tässä tapauksessa t: 2 grammaa.

Siksi määrittelemme C: n massan osuudet näissä kolmessa yhdisteessä:

• T₂C: 1 gramma c/2 grammaa t
• TC: 2 grammaa c/2 grammaa t
• T₂C₃: 3 grammaa c/2 grammaa t

Meillä on suhde C: n massaan, joka on yhtä suuri kuin 1: 2: 3. Toisin sanoen TC: ssä on 2 kertaa enemmän c kuin t₂C, ja 3 kertaa enemmän C: ssä₂C₃ kuin t₂C. Kuten voidaan nähdä, 1: 2: 3 ovat pieniä kokonaislukuja (ne eivät edes ylitä kymmenen).

Esimerkkejä useiden mittasuhteiden laista

Seuraavia esimerkkejä varten sovelletaan samoja aiempia vaiheita, mutta otamme huomioon vastaavien elementtien molaariset massat olettaen, että yksi mooli yhdistettä.

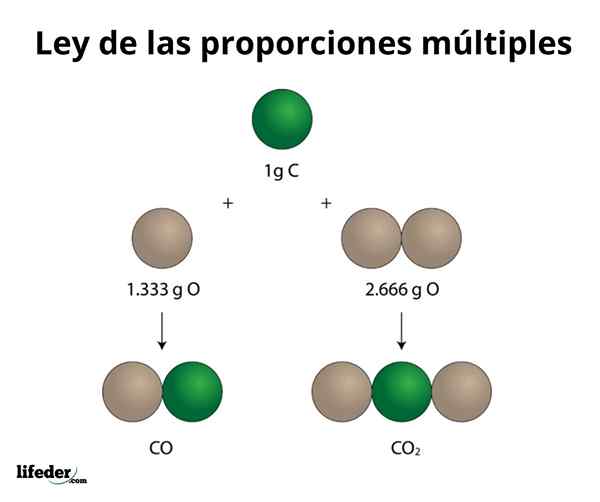
Kookospähkinä₂

Tämä esimerkki selittää yksinkertaisella tavalla, miten useiden mittasuhteiden laki toimii; CO: ssa (hiilimonoksidi) on 1.333 grammaa happea jokaiselle hiilen grammalle. Hiilidioksidissa (CO₂) on 2.666 grammaa happea jokaiselle hiilen grammalle. Siksi hapen osuus molemmissa yhdisteissä on 1: 2, pieni kokonaisluku.

H₂VAI NIIN₂JOMPIKUMPI₂

Usean mittasuhteen laki koskee H -paria₂VAI NIIN₂JOMPIKUMPI₂.

Voi palvella sinua: 30 esimerkkiä kemiallisista suspensioista

H: n moolissa₂Tai 2 grammaa vetyä yhdistetään 16 grammaan happea. Samaan aikaan H: n mol₂JOMPIKUMPI₂, 2 grammaa vetyä yhdistetään 32 grammaan happea. Varmistaaksesi, onko tämä laki täytetty, meidän on asetettava sama massa yhdelle elementeille molemmissa yhdisteissä. Tämä aika on vety: 2 grammaa.

Mastosuhteet H: lle₂Tai h₂JOMPIKUMPI₂ ovat:

• H₂O: 16 grammaa tai/2 grammaa H
• H₂JOMPIKUMPI₂: 32 grammaa tai/2 grammaa H

O: n massan suhde on 16:32. Voimme kuitenkin yksinkertaistaa sitä jakamalla 16: lla, pysymällä 1: 2. Lopullinen suhde koostuu jälleen pienistä kokonaislukuista.

Sw₂-Sw₃

SO -moolissa₂, 32 grammaa rikkiä yhdistetään 32 grammaan happea. Sillä välin niin moolissa₃, 32 grammaa rikkiä yhdistetään 48 grammaan happea. Rikkimassa on sama molemmille yhdisteille, joten voimme suoraan verrata happea:

• Sw₂: 32 grammaa tai
• Sw₃: 48 grammaa tai

On happimassan suhde molempien yhdisteiden välillä, joka on yhtä suuri kuin 32:48 tai 1: 1.5. Mutta ei ollut olemassa, että kokonaisia ​​numeroita pitäisi olla? Suhde 1: 1.5 (1/1.5) Se voidaan kirjoittaa myös nimellä 2: 3 (0.6), ja taas meillä on pienet kokonaisluvut: 2 ja 3.

Huomaa, että olisimme myös kirjoittaneet suhteen 48:32 tai 1.5: 1, tulos 3: 2. Laki ei muutu, vain suhteen tulkinta: on 1.5 tai 3/2 kertaa enemmän happea SO: ssa₃ että niin₂; mikä on sama sanottava, että on 2/3 tai 0.6 kertaa vähemmän happea SO: ssa₂ että niin₃.

EI EI₂-N₂PÄÄLLÄ₂JOMPIKUMPI₃-N₂JOMPIKUMPI₅

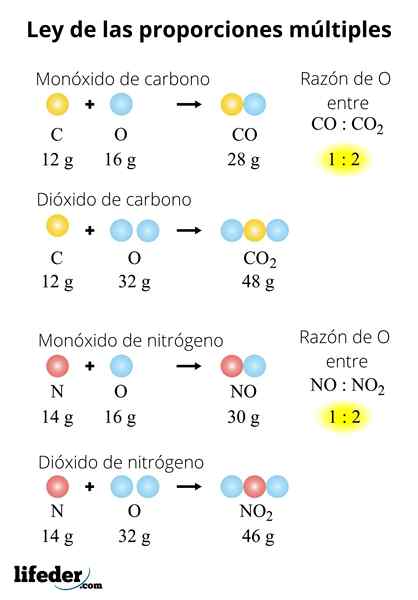
Lakia voidaan soveltaa myös yhdisteiden sarjaan. Harkitse typpioksideja: ei-ei₂-N₂PÄÄLLÄ₂JOMPIKUMPI₃-N₂JOMPIKUMPI₅. Tämän lain arvioimiseksi meidän on asetettava massa typpeä: 28 grammaa. Koska? Koska ei ja ei₂ Heillä on typpiatomi vähemmän kuin muut oksidit:

• 2 (ei): 28 grammaa n/32 grammaa tai
• 2 (ei₂): 28 grammaa N/64 grammaa tai
• N₂O: 28 grammaa n/ 16 grammaa tai
• N₂JOMPIKUMPI₃: 28 grammaa n/ 48 grammaa tai
• N₂JOMPIKUMPI₅: 28 grammaa n/ 80 grammaa tai

Se voi palvella sinua: Aivolisäkkeen happo (H3PO2): Ominaisuudet, käytöt ja reagenssit

Unohdetaan typpi ja keskitytään hapen grammiin:

• 2 (ei): 32 grammaa tai
• 2 (ei₂): 64 grammaa tai
• N₂O: 16 grammaa tai
• N₂JOMPIKUMPI₃: 48 grammaa tai
• N₂JOMPIKUMPI₅: 80 grammaa tai

On 32: 64: 16: 48: 80: n massojen suhde tai yhtä suuri kuin. Sen yksinkertaistamiseksi jaamme kaikki sen numerot pienimpiin, 16: een, koska se on 2: 4: 1: 3: 5.

Eli on: 2 kertaa enemmän happea ei kuin n₂Tai 4 kertaa enemmän happea ei₂ että n₂Tai 3 kertaa enemmän happea n₂JOMPIKUMPI₃ että n₂Tai ja 5 kertaa enemmän happea n₂JOMPIKUMPI₅ että n₂JOMPIKUMPI. Jälleen meillä on pieniä kokonaislukuja, jotka vaihtelevat välillä 1-5.

Rajoitukset

Useiden mittasuhteiden lakia ei aina täytetä. Esimerkiksi elementtien molaarimassat tai atomipainot eivät ole kokonaisia ​​lukuja, mutta niissä on monia desimaaleja. Tämä muuttaa kokonaan laskettuja suhteita, jotka lakkaavat olevan yksinkertaisia.

Samoin lakia ei täytetä raskaille yhdisteille, kuten joillekin hiilivedyt. Esimerkiksi undercano, c_yksitoistaH₂₄, on 1.0083 tai 121/120 kertaa enemmän vetyä kuin dekaani, c₁₀H₂₂, jonka suhde koostuu 121 ja 120, jotka ylittävät kymmenen; Ne eivät ole pieniä kokonaisia ​​lukuja.

Ja lopuksi, laki epäonnistuu ei -stoikiometristen yhdisteiden kanssa, kuten monien oksidien ja sulfidien kanssa.

Johtopäätös

Usean mittasuhteiden laissa todetaan, että kun kaksi elementtiä muodostavat useamman kuin yhden yhdisteen, elementin eri massot, jotka yhdistyvät toisen elementin saman massan kanssa, ovat suhteessa pienestä määrästä.

Viitteet

1. Whitten, Davis, Peck & Stanley. (2008). Kemia. (8. ed.-A. Cengage -oppiminen.
2. Wikipedia. (2020). Usean mittasuhteen laki. Haettu: vuonna.Wikipedia.org
3. Enyclopaedia Britannica -toimittajat. (2020). Usean mittasuhteen laki. Toipunut: Britannica.com
4. Kemia. (4. kesäkuuta 2019). Daltonin monien mittasuhteiden laki. Palautettu: ChemistryGod.com
5. Garcia Nissa. (2020). Useiden mittasuhteiden laki: Määritelmä ja esimerkki. Opiskelu. Toipunut: Opiskelu.com