De Morgan -laki

Selitämme, mitkä ovat Morganin lait, esittelemme ne ja laitamme esimerkkejä

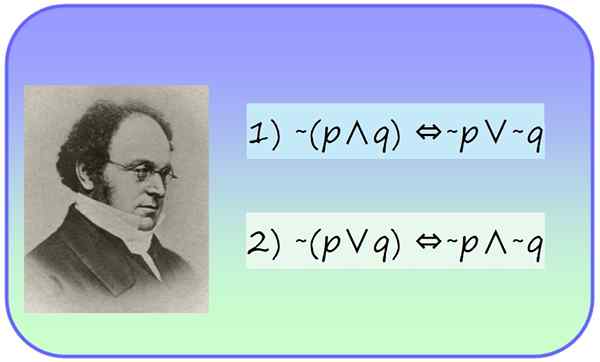Kuvio 1.- Morganin matemaatikko Augustus (1806-1871) ja hänen ehdotuslogiikan lait. Lähde: f. Zapata.

Mitkä ovat de Morganin lait?

De Morganin lait ovat kaksi loogista lakia, jotka kuuluvat ehdotuslogiikkaan, jonka Englannin matemaatikko Augustus on Morgan (1806-1871). He määrittelevät seuraavat yhdistetyn loogisen ehdotuksen suhteen:

1. Konjunktion vastakohta vastaa disjunktiota, joka muodostuu vastakohtien tai ehdotusten kieltäytymisten kanssa, jotka muodostavat konjunktion.
2. Disjunktion kieltäminen voidaan ilmaista konjunktiona, joka koostuu disjunktiossa olevien ehdotusten vastakohdista tai kieltäytymistä.

Ehdotuslogiikan merkinnässä De Morganin lait ilmaistaan ​​kompaktilla ja muodollisemmalla tavalla näin:

1. ∼ (p ∧ q) ⇔ ∼P ∨q
2. ∼ (p ∨ q) ⇔ ∼P ∧q

Nämä lait ilmaisevat, että joko konjunktion tai disjunktion kieltämisessä tulos vastaa jokaisen osallistuvan ehdotuksen kieltämistä erikseen ja sijoittamalla ne yhdistävät liittimen, joka yhdistää ne.

De Morganin lakien paremmin ymmärtämiseksi on tarpeen tarkistaa ehdotusten ja symbolien merkitys, jota käytetään ehdotuslogiikassa, nähdä kuinka nämä lait sovelletaan kätevästi.

Looginen merkintä

Ehdotuslogiikan perustyökalu on ehdotukset. Looginen ehdotus on lausunto, joka myöntää a todellinen arvo, Onko se totta vai väärä, mutta ei molemmat samanaikaisesti. Tässä ei ole epäselvyyttä, ts.

Ehdotus on merkitty pienillä kirjaimilla, kuten seuraavissa esimerkeissä:

• K: Mexico City on Meksikon pääkaupunki (totta).
• K: Lisäämällä 2 ja 3, 4 (väärä) saadaan.
• V: Kaikki nisäkkäät ovat maaeläimiä (vääriä).

Voi palvella sinua: Heptagon

On myös monimutkaisempia ehdotuksia, jotka on rakennettu käyttämällä yksinkertaisia ​​ehdotuksia, kuten nämä:

• K: Carlos menee elokuvateatteriin, jos ei sataa.
• K: ANA on kemisti tai meribiologi.
• V: Juan on menossa illalliselle tai Pedro näkee pelin televisiossa.

Loogiset liittimet

Loogiset liittimet ovat symboleja, joita käytetään yksinkertaisten ehdotusten linkittämiseen ja siten monimutkaisempien ehdotusten rakentamiseen. Ehdotuslogiikassa jokaisella on erityinen merkitys.

Käytetyimmät liittimet ovat konjunktio, disjunktio, yksinoikeudellinen disjunktio, kieltäminen, ehdollisuus ja bi-conditionality.

Konjunktio

Konjunktio on merkitty käänteisellä "V" -kirjeellä. Komposiittiehdotus konjunktion kautta symboloidaan p ∧ q, seuraavasti:

• P ∧ K: Meksiko on Meksikon pääkaupunki ja on Pohjois -Amerikassa.

Tässä on helppo tunnistaa, että P on "Mexico City on Meksikon pääkaupunki" ja Q Is "on Pohjois -Amerikassa".

Erottelu

Kaksi tyyppiä disjunktiota erottuvat: heikko ja yksinoikeus. Eräs heikko Sitä symboloi ∨ ja loogisessa merkinnässä se olisi p ∨ q. Esimerkki tällaisesta disjunktiosta on:

• P ∨ K: Juan on jalkapalloilija tai Juan on tennispelaaja.

Sen sijaan yksinoikeus Sitä symboloi merkki ⊻ ja tarkoittaa, että esimerkiksi yksi ehdotuksista on suljettava pois:

P ⊻ K: Alicia on 20 -vuotias tai Alicia on 22 -vuotias.

Ero molempien tyyppien välillä on selkeä, yksinoikeudella disjunktiossa yksi ehdotuksista on suljettu pois, koska jos Alicia on 20 -vuotias, hän ei voi olla 22 ja päinvastoin. Toisaalta, heikolla disjunktiossa, Juan voi olla jalkapalloilija ja tennispelaaja samanaikaisesti.

Kieltäminen

Laittamalla symbolin ∼ ehdotus, tämä kielletään, kuten:

• K: ∼ (Veracruz on Meksikon pääkaupunki).

Se luetaan nimellä "Veracruz ei ole Meksikon pääkaupunki". Muita tapoja ilmaista kieltäytyminen, lukuun ottamatta "ei", on ilmausten, kuten "on väärä", "se on valhe, että" ja "ei ole totta, että".

Voi palvella sinua: lineaarinen interpolointi

Ehdollisuus

Ne ovat yhdistelmäehdotuksia, jotka yleensä käyttävät sanoja "kyllä" ja "sitten ..." linkittääkseen kaksi ehdotusta, joissa on ehdollisuus tai seuraamus. Ehdotuksen osa, joka on kirjoitettu heti "kyllä" edeltäjä Aalto hypoteesi ehdotuksesta ja siitä, mikä on termin "silloin" johtopäätös jompikumpi seurauksena oleva.

Ehdollisuuteen käytetty symboli on nuoli vasemmalta oikealle "→", joten kahden ehdotuksen välinen ehdollisuus esitetään p → q, joka voidaan lukea nimellä "Jos p, niin Q". Esimerkiksi:

P → K: Jos sataa iltapäivällä, en pelaa tennistä.

Kaksoissuuntaisuus

Tämän tyyppisessä ehdotuksessa käytetään ilmausta ”kyllä ​​ja vain jos” kahden ehdotuksen yhdistämiseksi, joita kutsutaan ensimmäiseksi ja toiseksi biconditional -jäseneksi. Käytetty symboli on kaksisuuntainen nuoli "↔".

Kaksi ehdotusta, jotka on kytketty "kyllä, ja vain jos" kutsutaan vastaavasti ensimmäinen ja toinen jäsen ja kahden ehdotuksen p ja q bi-ilmastointi pysyvät p ↔ q. Esimerkiksi:

P ↔ K: Maria haluaa ajaa pyörällä vain ja vain jos päivä on aurinkoinen.

De Morganin lakien osoittaminen

De Morganin lait ovat osa loogisia ekvivalensseja, ja ne voidaan osoittaa totuustaulukoiden kautta, joita käytetään ehdotuksen totuuden (todellinen tai väärän) arvon tuntemiseen.

Koska konjunktio on totta vain silloin, kun p ja q ovat totta, sen totuustaulukko on:

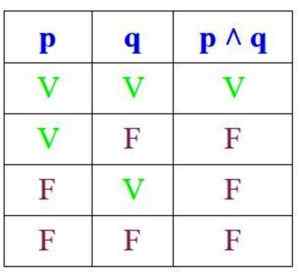
Toisaalta, erimielisyydessä, ehdotus on totta, jos p ja q ovat totta tai jos ainakin yksi niistä on, mutta se on väärä, jos molemmat ovat:

Voi palvella sinua: Permutaatiot ilman toistamista: kaavat, esittely, harjoitukset, esimerkit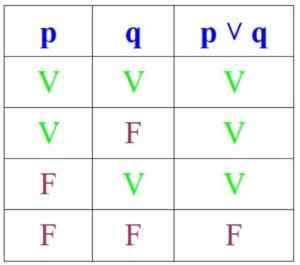

Nyt kieltäminen muuttaa totuuden vääriksi ja päinvastoin. Tässä tapauksessa totuuden arvot (p ∧ q) ja ∼ (p ∨ q) ovat totuuden arvojen (p ∧ q) ja (p ∨ q) vastakohta:

Ja on varmistettava, että nämä tulokset saadaan suoritettaessa vastaavia totuustaulukoita (∼ p ˅ ∼ q) ja (∼ p ˄ ∼ q):

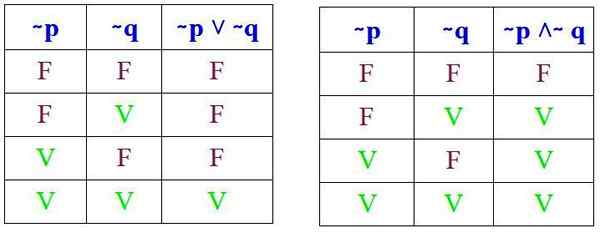
Ja todellakin, kun verrataan vastaavia totuustaulukoita, havaitaan, että De Morganin lait täytetään. Nyt kaksi esimerkkiä sen hakemuksesta nähdään.

Ratkaistu esimerkki 1

Käytä de Morganin lakeja löytääksesi vastaavan ekspression: ∼ (∼P ˅ ∼Q)

• Ratkaisu

Annetusta ekspressiosta verrataan ∼ (∼P ˅ ∼Q) Morganin lakiin:

∼ (p ∨ q) ⇔ ∼P ∧q

Ja havaitaan, että kieltäminen on jo sulkeiden ulkopuolella molemmissa tapauksissa, joten lain ohjeita noudatetaan: se kieltäytyy ∼P, kiistää ∼Q: n ja liitin muuttuu:

∼ (∼P ˅ ∼Q) ⇔ ∼ (∼P) ∧ ∼ (∼Q) ⇔ P ∧ Q

Ratkaistu esimerkki 2

Määritä quivalent -ekspressio ∼ [∼P ˄ ∼ (∼Q)] ≡

• Ratkaisu

Ensinnäkin ∼Q: n kieltäminen yksinkertaistetaan:

∼ [∼ -P ˄ ∼ (∼Q)] ⇔ ∼ [∼P ˄ Q]

Koska kiinnikkeen ulkopuolella on jo kieltäminen, tuloksena olevaa ilmaisua verrataan Morganin lakiin: ∼ (p ∧ q) ⇔ ∼P ∨q

Ratkaisemaan ∼ [∼P ˄ q] sinun on kiellettävä ∼P, kiistä q ja vaihdettava liitin:

∼ [∼P ˄ q] ⇔∼ (∼P) ∨ ∼Q ⇔ P ˅ ∼Q

Viitteet

1. Becerra, J.M.  UNAM -logiikan muistiinpanot.
2. Loistava. Morganin laeista. Toipunut: loistava.org.
3. Elektroniikkaoppaat. Morganin lause. Toipunut: Elektroniikka-Tormales.WS.
4. López, f. Johdatus matemaattiseen logiikkaan. Palautettu: YouTube.com
5. Muñoz, c. Johdanto logiikkaan. Haettu: verkkosivustot.UCM.On.